Программа по математике GeoGebra — инструкция как пользоваться
Возникали ли у вас необходимость построить график функции? Поможет бесплатная программа по математике GeoGebra. Она анализирует функции, решает задачи, строит графики. Рассмотрим подробно, как установить, скачать и работать с этой программой.
Что это такое
GeoGebra — программа по математике. Написана на языке программирования Java. Разработана Маркусом Хохенвартером. Приложение не ограничивается только работой с графиками. Используйте ее для создания чертежей, решении задач по геометрии, разработке анимации.
Позволяет наглядно обучаться математике.
Читайте также:
Решает такие задачи:
- Обучение алгебре и геометрии;
- Создание графиков и таблиц;
- Работа со статическими данными;
- Анимация;
- Создание 2D, 3D фигур;
- Создание интерактивных роликов с последующим размещением в интернет.
Готовый материал
- сохраните форматом GeoGebra;
- распечатайте;
- экспортируйте в форматах SVG, PNG, PDF.

По адресу: https://wiki.geogebra.org/ru/Руководство находится руководство пользователя, с информацией про работу с объектами.
Как скачать
Официальный сайт находится по адресу: http://www.geogebra.org.
Программу можно скачать и установить на ПК. Также разработчики предлагают online использование.
Чтобы скачать нажимаем ссылку «Загрузки».
Будет предложено два варианта:
- Graphing Calculator. Используйте ее для решения уравнений, нахождение специальных функций, возможность поделиться результатами с другими людьми;
- Geometry. Для создания геометрических фигур, рисования.
Разработчики предлагают:
- Скачать приложения для ОС Windows, Mac бесплатно на русском.
- Установить расширения в браузер Chrome,
- Загрузить приложения для работы на смартфонах и планшетах.
Скачиваем инсталляционный «exe» файл. Нажимаем по нему мышкой два раза для начала загрузки. Установка простая, не вызовет сложностей даже у начинающий пользователей. » обозначает степень.
» обозначает степень.
Добавляйте переменные. Пропишите их в строку формулы.
Как создать 3D
В настройках переходим «Apps»-«3D». Выбираем инструменты кликнув по иконке. Далее постройте объект следуя подсказкам.
Выполняем нужные действия.
GeoGebra online на русском
Не хотите загружать дополнительный софт? Используйте онлайн (online) версию, расположенную по адресу: https://www.geogebra.org/classic. Единственное условие необходимое для работы — наличие интернет.
Вывод
GeoGebra с широким функционалом, предназначена для обучения алгебре и геометрии. Если не удалось установить ее на ПК, используйте online версию. Мне кажется она удобнее. Остались вопросы, инструкция по работе с GeoGebra поможет разобраться детальнее.
Начало работы с Geogebra. Добавление и знакомство с интерфейсом.
Добавление GeoGebra в SMART Notebook
- Нажмите кнопку Add-ons («Надстройки») , затем нажмите GeoGebra.
- Выберите пункт «Вставить виджет GeoGebra»
Если вы хотите использовать материалы из коллекции GeoGebraTube, введите ключевое слово в поле «Поиск в материалах GeoGebra», а затем нажмите «Поиск».
 На текущей странице SMART Notebook появится рабочий лист.
На текущей странице SMART Notebook появится рабочий лист.Интерфейс основного виджета GeoGebra
Рис 1. Интерфейс основного виджета GeoGebra (по умолчанию)Основное меню
Основное меню всегда располагается в правом верхнем углу окна GeoGebra и содержит следующие пункты:
- Файл (создание, открытие и предоставление доступа к материалам GeoGebra)
- Правка (копировать и вставить объект, выбрать все объекты)
- Перспективы (изменение режима GeoGebra)
- Вид (настройка интерфейса виджета GeoGebra, добавление окон вида)
- Настройки (изменение параметров отображения элементов виджета: размер шрифта, язык интерфейса и т.д.)
- Справка (доступ к справочным материала на портале разработчика GeoGebra)
- Войти (вход в аккуант GeoGebra)
Панель инструментов Каждый режим содержит собственную панель инструментов, необходимых для работы в данном виде.
 Для активации инструмента достаточно нажать на соответствующий значок. Команды на панели инструментов объединены в группы, содержащие схожие инструменты. Так, например, в группе прямых можно построить параллельную прямую, перпендикуляр, касательную, поляру и так далее.
Для активации инструмента достаточно нажать на соответствующий значок. Команды на панели инструментов объединены в группы, содержащие схожие инструменты. Так, например, в группе прямых можно построить параллельную прямую, перпендикуляр, касательную, поляру и так далее.При выборе инструмента в нижней части окна GeoGebra появляется подсказка, объясняющая как использовать данный инструмент. Например, для построения параллельной прямой надо выбрать точку, через которую будет проходить новая прямая, а затем указать прямую, которой она должна быть параллельна.Режимы работы (Перспективы)GeoGebra позволяет работать в шести различных режимах. Выбор режима работы осуществляется, через пункт Основного меню — Перспективы.
Алгебра
Режим Алгебра и графика разделен на две области — Алгебраический вид и Графический вид (см. рис. 1). По умолчанию в графическом виде отображается система координат. Вы можете создавать объекты на координатной плоскости, а в окне Алгебраического вида будут отображаться количественные характеристики: координаты точки, уравнения, задающие данные объекты и т.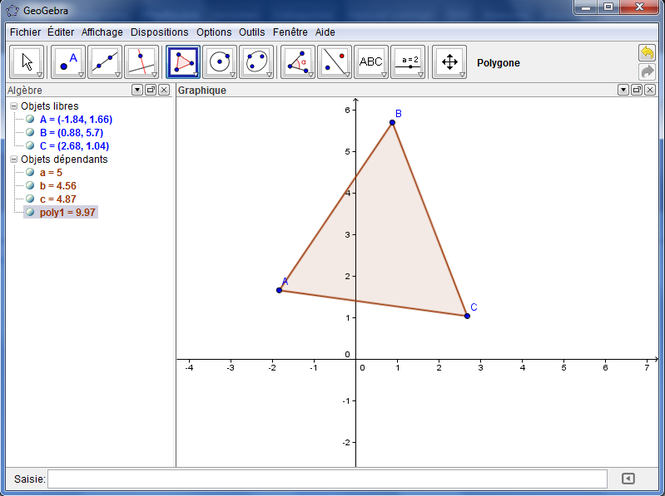 д.
д.Геометрия
Режим Геометрия идентичен графическому виду режима Алгебра и графики. По умолчанию в графическом виде режима Геометрия система координат не отображается.Spreadsheet (электронные таблицы)
Режим Электронные таблицы состоит из двух окон — Электронной таблицы и Графического вида. По умолчанию в графическом виде отображается система координат. Работа с таблицами представляет собой упрощенный функционал редактора электронных таблиц, такого например, как Excel.CAS (система символьных вычислений)
Режим CAS состоит из двух окон — CAS и Графического вида. Режим предназначен для упрощения выражений, проведения вычислений, разложение на множители, работы с матрицами, вычисление производной и интеграла и т.д. По умолчанию в графическом виде отображается система координат.3D Graphics (Стереометрия)
 По умолчанию в графическом виде отображается прямоугольная система координат в пространстве.
По умолчанию в графическом виде отображается прямоугольная система координат в пространстве.Probability (Вероятность и статистика)
В режиме Вероятность и статистика отображается Калькулятор вероятности, который позволяет быстро посчитать и визуализировать распределение вероятности.Виртуальная клавиатура и строка ввода
В виджете GeoGebra алгебраический ввод встроен в окно Алгебраического вида. Вы можете начать ввод команды в поле рядом со знаком , поэтому по умолчанию отдельная строка ввода не отображается. Её можно включить через пункт
Виртуальная клавиатура обеспечивает эту же функциональность, но содержит также упрощенный редактор формул, что облегчает процесс ввода, находясь у доски.
| Виртуальная клавиатура | Строка ввода |
Cтрока ввода
В GeoGebra действие каждого инструмента можно заменить соответствующей командой, вводимой в окне алгебраического ввода, таким образом, для выполнения построений можно вообще не использовать мышь.
Не для всех команд есть графический инструмент, некоторые операции можно выполнить только путем ввода команды.
Панель Стили
С помощью данной панели вы можете изменять цвет, размер и стиль объекта. Содержимое панели Стилей зависит от того, какой объект был выбран. Также можно заблокировать объект от случайных изменений, нажав кнопкуВ GeoGebra каждый объект имеет уникальное имя, которое может отображаться как подпись в окне графического вида, также может отображаться количественная характеристика объекта: координаты, длина, площадь, объем. С помощью панели Стилей вы можете указать форму отображения надписи, через пункт Надпись. Доступ к расширенной настройке по каждому объекту возможен через кнопку Настройки на панели Стилей. А кнопка Виды, позволяет быстро добавить еще один вид в окно GeoGebra.
Шаги построения и протокол
Добавление этих элементов интерфейса возможно через пункт Основного меню – ВидПротокол построения
Протокол построения представляет детализированную информацию о шагах построения чертежа, с указанием имени объекта его определения и количественной характеристики.
Шаги построения
Панель Шаги построения позволит просмотреть ход построения вашего чертежа шаг за шагом. Действие кнопок описано на рисунке ниже.
Программа по математике GeoGebra — инструкция как пользоваться
GeoGebra — вычислительная программа на компьютер для математических вычислений любого уровня образования, объединяющая в себе геометрию с алгеброй, электронные таблицы и графику, вычислительную статистику.
GeoGebra — это не просто многофункциональная математическая программа для компьютера, это мировое сообщество миллионов пользователей, которое активно растёт.
Динамическое ПО от разработчиков GeoGebra, которые поддерживают науку и передовые технологии, инновационные инфо-продукты и математическое образование. Утилита связывает геометрию и алгебру в визуально понятной форме. Математика это не только формула на листе бумаги, с ГеоГебра её можно ощущать визуально. Для учителей это неотъемлемый помощник по ходу обучения.
Основные возможности GeoGebra:
- построение графиков функций, кривых, параметрических координат, конических сечений;
- создание окружностей по радиусу и трём точкам, эллипсов, парабол, гипербол;
- моделирование 3D-объектов;
- сложение и умножение матриц;
- транспортирование, инвертирование, вычисление определителя и комплексных чисел;
- нахождение точек пересечения кривых и другие.
Скачать GeoGebra бесплатно на русском
Загрузить утилиту можно абсолютно бесплатно с официального сайта разработчика по ссылкам ниже.
В ГеоГебра доступны дополнительные функции:
- Статическое вычисление математического ожидания или дисперсии, а также коэффициента корреляции.
- Аппроксимация нескольких точек в кривой по заданному виду.
- Работа с таблицами и анимацией, ввод команд.
- Доступны инструменты редактирования Перо, Удаление, Полигон и другие.
С GeoGebra можно создавать вычисления онлайн и строить сложные графики прямо на сайте. Прямая ссылка доступна ниже.
Прямая ссылка доступна ниже.
Рекомендуется скачать GeoGebra бесплатно на русском языке для того, чтобы создавать Java-апплеты на динамических чертежах, а после включать их на сайты (html-страницы). С официального сайта можно подгрузить бесплатно готовые шаблоны в формате ggb прямо в ГеоГебру.
Возникали ли у вас необходимость построить график функции? Поможет бесплатная программа по математике GeoGebra. Она анализирует функции, решает задачи, строит графики. Рассмотрим подробно, как установить, скачать и работать с этой программой.
Содержание
Что это такое
GeoGebra — программа по математике. Написана на языке программирования Java. Разработана Маркусом Хохенвартером. Приложение не ограничивается только работой с графиками. Используйте ее для создания чертежей, решении задач по геометрии, разработке анимации.
Позволяет наглядно обучаться математике.
Читайте также:
- Создание графика в Word;
- Как работать с рисованной анимацией.
Решает такие задачи:
- Обучение алгебре и геометрии;
- Создание графиков и таблиц;
- Работа со статическими данными;
- Анимация;
- Создание 2D, 3D фигур;
- Создание интерактивных роликов с последующим размещением в интернет.
Готовый материал
- сохраните форматом GeoGebra;
- распечатайте;
- экспортируйте в форматах SVG, PNG, PDF.
По адресу: https://wiki.geogebra.org/ru/Руководство находится руководство пользователя, с информацией про работу с объектами.
Как скачать
Официальный сайт находится по адресу: http://www.geogebra.org. Программу можно скачать и установить на ПК. Также разработчики предлагают online использование. Чтобы скачать нажимаем ссылку «Загрузки». Будет предложено два варианта:
- Graphing Calculator. Используйте ее для решения уравнений, нахождение специальных функций, возможность поделиться результатами с другими людьми;
- Geometry.
 Для создания геометрических фигур, рисования.
Для создания геометрических фигур, рисования.
Разработчики предлагают:
- Скачать приложения для ОС Windows, Mac бесплатно на русском.
- Установить расширения в браузер Chrome,
- Загрузить приложения для работы на смартфонах и планшетах.
Скачиваем инсталляционный «exe» файл. Нажимаем по нему мышкой два раза для начала загрузки. Установка простая, не вызовет сложностей даже у начинающий пользователей.
Интерфейс
Напоминает графический редактор. Рассмотрим его основные элементы:
- Кнопка меню (три горизонтальные линии). Используйте для изменения настроек;
- Панель инструментов. Для создания фигур и графиков;
- Стрелки отменяющие действия;
- Рабочая область. Все действия происходят в ней. При помощи колеса мыши редактируйте масштаб.
Чтобы настроить приложение для работы, сделайте следующее. Нажимаем кнопку настроек (три горизонтальные линии)-«Apps». Выбираем необходимое: калькулятор, геометрия, 3D. » обозначает степень.
» обозначает степень.
Добавляйте переменные. Пропишите их в строку формулы.
Как создать 3D
В настройках переходим «Apps»-«3D». Выбираем инструменты кликнув по иконке. Далее постройте объект следуя подсказкам. Выполняем нужные действия.
GeoGebra online на русском
Не хотите загружать дополнительный софт? Используйте онлайн (online) версию, расположенную по адресу: https://www.geogebra.org/classic. Единственное условие необходимое для работы — наличие интернет.
Вывод
GeoGebra с широким функционалом, предназначена для обучения алгебре и геометрии. Если не удалось установить ее на ПК, используйте online версию. Мне кажется она удобнее. Остались вопросы, инструкция по работе с GeoGebra поможет разобраться детальнее.
GeoGebra – уникальная программа по математике. Она написанная и усовершенствованная на программном языке Java. Это приложение не ограничивается одной лишь графикой, а имеет в себе множество опций. В основному, GeoGebra используется для различных чертежей, для решений задач по геометрии и их аккуратного оформления.
Готовый материал, который прошел GeoGebra можно распечатать, сохранить специальным форматом GeoGebra или же экспортировать на нужный носитель информации.
Скачать бесплатно GeoGebra 6.0.564
Прошлые версии
GeoGebra 6.0.562
GeoGebra 6.0.560
GeoGebra 6.0.559
GeoGebra 6.0.546
GeoGebra 6.0.544
GeoGebra 6.0.541 Repack
GeoGebra 6.0.535 Repack
GeoGebra 6.0.533
[свернуть]
Пароль ко всем архивам: 1progs
Видео по установке GeoGebra
GeoGebra поможет решить такие задачи:
- обучит математическим наукам;
- создаст идеальные графики, а также таблицы;
- создаст сложную многофункциональную анимацию;
- создаст яркие интерактивные ролики с последующим размещением в интернете.
Программу GeoGebra можно скачать бесплатно на русском языке. Также разработчики предлагают использование программы в режиме online. Classic GeoGebra устанавливается, как и обычный файл и сохраняется на указанном диске. 3D–графики идеально смотрятся в распечатанном виде или же на сенсорной доске.
Classic GeoGebra устанавливается, как и обычный файл и сохраняется на указанном диске. 3D–графики идеально смотрятся в распечатанном виде или же на сенсорной доске.
Также приложение можно скачать на телефон или же планшет. Это никаким образом не скажется на скорости работы. Можно потом готовый файл сбросить на компьютер или же просто распечатать с телефона.
Скачать торрент GeoGebra 6.0.564 3D на русском
Аналоги программы
Похожие программы смотрите в наших подборках программ
Программы для обучения
Используемые источники:- https://soft-file.ru/geogebra/
- https://public-pc.com/instruktsiya-po-rabote-s-geogebra/
- https://1progs.ru/geogebra/
Программа по математике GeoGebra — инструкция как пользоваться
Графический калькулятор
В этой заметке рассмотрим Графический калькулятор
Экран разбит на несколько областей, аналогично тому как это сделано в Desmos. Слева расположена панель для ввода уравнений (панель объектов), в центре отображаются графики и объекты (полотно), внизу всплывающая панель виртуальной клавиатуры, вверху — панель инструментов, справа — свойства выбранной фигуры. Есть и другие панели, отображение которых пока не будем включать.
Слева расположена панель для ввода уравнений (панель объектов), в центре отображаются графики и объекты (полотно), внизу всплывающая панель виртуальной клавиатуры, вверху — панель инструментов, справа — свойства выбранной фигуры. Есть и другие панели, отображение которых пока не будем включать.
Литература
- С. В. Ларин. «Компьютерная анимация в среде GeoGebra на уроках математики»,
Легион, г. Ростов-на-Дону, 2020. - Р. А. Зиатдинов. О возможностях использования интерактивной геометрической среды Geogebra 3.0 в учебном процессе.
//Материалы 10-й Международной конференции «Системы компьютерной математики и их приложения» (СКМП-2009), СмолГУ, г. Смоленск, 2009, C. 39-40 (PDF, 122 Kb (недоступная ссылка)).
- Р. А. Зиатдинов. Геометрическое моделирование и решение задач проективной геометрии в системе GeoGebra.
//Материалы конференции «Молодежь и современные информационные технологии», Томский политехнический университет, г. Томск, 2010, C. 168-170 (PDF, 10.2 Mb).
Томск, 2010, C. 168-170 (PDF, 10.2 Mb).
- Д. Мартинович, З. Карадаг, Д. Макдугалл (ред.). //Материалы второй Северо-Американской конференции GeoGebra, Университет Торонто, Канада, 2011, (PDF, 2.18 Mb).
- Р. А. Зиатдинов, В.М. Ракута. (2012). Системы динамической геометрии как средство компьютерного моделирования в системе современного математического образования. European Journal of Contemporary Education 1(1), 93-100 (PDF, 311 Kb).
- И.Б. Гарипов, Р.М. Мавлявиев, Э.Д. Хусаинова. (2012). Использование динамической геометрической среды GeoGebra в изучении функционально-графических методов при решении задач с параметрами. Материалы третьего Российского научного семинара «Методы информационных технологий, математического моделирования и компьютерной математики в фундаментальных и прикладных научных исследованиях» (в рамках международной конференции ИТОН-2012), с. 44-46 (PDF, 298 Kb).
- Р. А. Зиатдинов, Д. Джарвис. (2013). От редакторов специального выпуска.
 European Journal of Contemporary Education 4(2), 68-71 (PDF, 311 Kb).
European Journal of Contemporary Education 4(2), 68-71 (PDF, 311 Kb).
Панель инструментов
Геогебра предоставляет широкий спектр инструментов для графического представления объектов. Перечислим их в том же порядке, в котором расположены иконки.
Перемещение, фигура от руки
Режим перемещения позволяет выбирать и передвигать объекты мышкой и клавишами со стрелками. Клавиша Delete позволяет удалить выделенный объект или группу объектов. Перейти в режим перемещения можно нажатием клавиши Esc. Также в любом режиме можно перетаскивать фигуры правой кнопкой мыши
Пример. Введем функцию f(x) = x³ — 2x² в поле ввода текста; сразу же будет отображен график функции. Введем команду производная[f]. Снимем галочку «Закрепить объект» в свойствах этой кривой. Выберем режим «Перемещение». Будем перемещать график с помощью мыши и наблюдать за изменением уравнения функции и ее производной.
Фигура от руки и карандаш: Инструмент Карандаш — можно писать на чертеже как ручкой. В режиме «фигура от руки» каракули, нарисованные мышкой, волшебным образом превращаются в геометрические фигуры. Программа пытается угадать что нарисовано и преобразовать, угадывает даже некоторые функции.
В режиме «фигура от руки» каракули, нарисованные мышкой, волшебным образом превращаются в геометрические фигуры. Программа пытается угадать что нарисовано и преобразовать, угадывает даже некоторые функции.
Точка, пересечение, середина отрезка
Группа инструментов под названием Точка: Точка на объекте отличается от обычной точки тем, что при перемещении она ограничена контуром объекта-владельца. Команда: Point Команда для задания точки зависит от настроек, по умолчанию T = (x,y). Здесь вместо координат x, y могут быть числовые константы или другие переменные: T = (3, f(a)). Пересечение — позволяет создать точку пересечения двух выбранных объектов. Команда: Intersect
Примеры: Point[{1, 2}] — нарисовать точку с координатами (1,2). или просто S=(1,2) — нарисовать точку S с координатами (1,2)
Intersect — построить точку пересечения двух прямых, сами прямые нужно строить отдельными командами.
Более сложный пример. Зададим функцию параметрически, введем выражения a = Curve[cos(t), sin(t), t, 0, π] b = Curve[cos(t) + 1, sin(t), t, 0, π] и попробуем найти точку пересечения этих кривых a и b на отрезке от 0 до 2: Intersect[a, b, 0, 2]. Результат:
Зададим функцию параметрически, введем выражения a = Curve[cos(t), sin(t), t, 0, π] b = Curve[cos(t) + 1, sin(t), t, 0, π] и попробуем найти точку пересечения этих кривых a и b на отрезке от 0 до 2: Intersect[a, b, 0, 2]. Результат:
Символы x, y, z не нужно использовать для именования объектов. Эти имена зарезервированы для получения координат точки. Например: B = (x(T), s) — построить точку B с абсциссой, совпадающей с абсциссой точки T С = (5, y(T)) — построить точку С с абсциссой 5 и ординатой, совпадающей с ординатой точки T.
Команда для получения длины отрезка: Расстояние[M, C]
Команда для нахождения середины отрезка или центра коники: C=Середина(A,B) Команды: Midpoint, Length, Distance
Последние два инструмента для нахождения корней и точек экстремума выбранной функции:
Команды: Корень, Экстремум, НулиФункции, Min
Прямая, отрезок, луч, вектор
Набор инструментов для построения прямой, проходящей через две точки, отрезка по двум точкам, отрезка с заданной длиной, луча, вектора, ломаной линии. Команды: Прямая / Line, Отрезок / Segment, Луч / Ray, Вектор, Ломаная, Перенести
Команды: Прямая / Line, Отрезок / Segment, Луч / Ray, Вектор, Ломаная, Перенести
Перпендикулярная прямая, биссектриса, касательная
Набор инструментов позволяет построить: — перпендикулярную прямую, проходящую через заданную точку, к указанной прямой — параллельную прямую, проходящую через заданную точку, к указанной прямой — срединный перпендикуляр по двум точкам или к отрезку — биссектрису угла по трем точкам или двум прямым — касательную к окружности, конике или функции через точку — поляру или диаметр по точке или прямой, и конике.
Инструмент Аппроксимация позволяет построить линейную регрессию по набору точек. Пример: FitLine[{(-2, 1), (1, 2), (2, 4), (4, 3), (5, 4)}] результатом будет прямая y=0.4x+2 Синонимы ЛинейнаяАппроксимацияПоX, ЛинейнаяАппроксимацияПоY
Инструмент Локус.
Многоугольник
Набор инструментов позволяет построить: — многоугольник по заданным вершинам — правильный многоугольник по вершине, стороне и числу сторон — жесткий многоугольник — можно указать последовательно вершины, а можно кликнуть по существующему многоугольнику, чтобы сделать с него копию. — векторный многоугольник. Команды: Многоугольник
— векторный многоугольник. Команды: Многоугольник
Окружность, сектор, дуга
Набор инструментов для построения окружностей, заданных разными способами, дуг, секторов. Команды: Окружность, Полуокружность, СекторКруга, ОписаннаяДуга
Эллипс, парабола, коника
Набор инструментов для построения эллипса, гиперболы, параболы, коники по пяти точкам Команды: Эллипс, Гипербола, Парабола, Коника
Угол, наклон прямой, периметр, площадь
— Построение угла по трем точкам или двум прямым (указывать в порядке против часовой стрелки), угла заданной величины. — Расстояние между двумя точками, длина отрезка, периметр многоугольника, длина окружности или замкнутой кривой. — Площадь многоугольника, окружности или коники. — Наклон прямой (угловой коэффициент) — Создать список — щелкнуть по элементам, затем снова щелкнуть по иконке инструмента
Отношение объектов Инструмент позволяет выбрать два объекта и получить сообщение о равенстве некоторых величин этих объектов. * две прямые перпендикулярны? * две прямые параллельны? * два объекта равны? * прямая является касательной или секущей к конике? * точка лежит на прямой или конике?
* две прямые перпендикулярны? * две прямые параллельны? * два объекта равны? * прямая является касательной или секущей к конике? * точка лежит на прямой или конике?
Исследователь функции
Выбрать функцию, указать интервал, будет сформирована таблица с данными — точки экстремума, интеграл, площадь, корни, длина.
Команды: Угол, Повернуть, Расстояние, Периметр, Периферия, Наклон. Список обозначается фигурными скобками
Отражение, поворот, гомотетия
Отражение относительно прямой: выбрать исходный объект и прямую (отрезок) Отражение относительно точки: выбрать исходный объект и точку Отражение относительно окружности: Поворот вокруг точки: указать объект, центр вращения и угол поворота. Параллельный перенос по вектору: указать исходный объект и вектор переноса.
Гомотетия относительно точки: указать проектируемый объект, центр и коэффициент гомотетии.
Команды: Отразить, Повернуть, Перенести, Гомотетия
Ползунок, текст и другие элементы
Ползунок (слайдер) можно создать как с клавиатуры в панели объектов: ввести, например, a=2 и затем выбрать «Показывать объект», так и с помощью инструмента Ползунок.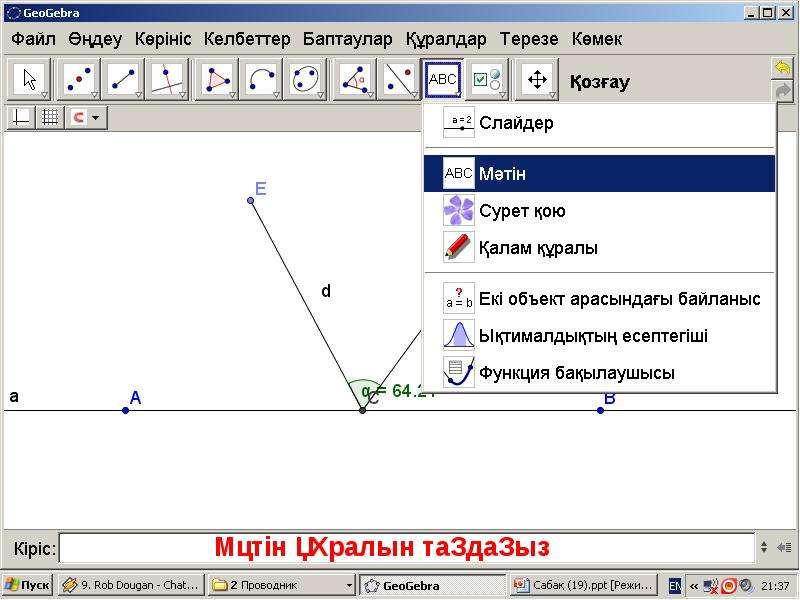 Вы можете изменять значение ползунка, передвигая его мышью или нажимая клавиши со стрелками. Пример. Ввести команды: A=(1,1) r=3 окружность(A,r) Будет создана точка A, ползунок r и окружность с центром в точке A и радиусом r, который можно менять вручную или включить анимацию. Ползунок скрыт на чертеже, при желании показать его щелкните по кружку слева от объекта. Ползунок может быть горизонтальным или вертикальным, регулируется скорость анимации, длина ползунка.
Вы можете изменять значение ползунка, передвигая его мышью или нажимая клавиши со стрелками. Пример. Ввести команды: A=(1,1) r=3 окружность(A,r) Будет создана точка A, ползунок r и окружность с центром в точке A и радиусом r, который можно менять вручную или включить анимацию. Ползунок скрыт на чертеже, при желании показать его щелкните по кружку слева от объекта. Ползунок может быть горизонтальным или вертикальным, регулируется скорость анимации, длина ползунка.
Изображение
Добавить на чертеж картинку из файла. Можно регулировать прозрачность. Можно сделать фоновым — тогда сетка просвечивает через рисунок.
Текст — создание надписи, пояснительного текста. Поддерживается latex. Надпись можно привязать к определенной точке на чертеже или к месту на листе, абсолютно или относительно — см. свойства. Для создания динамического текста, который будет отображать изменение параметров объекта, выберите объект из списка объектов. Имя объекта в поле ввода заключается в рамку, на чертеже будет показано значение объекта (например, для отрезка будет показана его длина). Правый клик по рамке позволяет переключаться между определением и значением объекта. Если перетащить объект из панели объектов на полотно, надпись будет создана автоматически.
Правый клик по рамке позволяет переключаться между определением и значением объекта. Если перетащить объект из панели объектов на полотно, надпись будет создана автоматически.
Можно выполнять алгебраические операции или применять команды к объектам, просто вписывая команды в текст. Результат операций будет динамически показан на чертеже. Пример. Ввести команды: a=10 b=30 c=a+b Объекты a и b будут преобразованы в ползунки. Перетащите последний объект на чертеж — будет создана надпись. По мере изменения параметров a и b с помощью ползунков сумма этих объектов будет автоматически отображаться на чертеже.
Команды: LaTeX, двойные кавычки
Доступны также такие элементы, как кнопка, флажок, окно ввода. Флажок можно использовать, например, для управления видимостью других объектов. С окном ввода связан другой объект, например, отрезок, и поле ввода будет управлять длиной этого отрезка.
Масштаб, перемещение полотна, скрытие объекта
Копировать стиль — выбрать объект-источник стиля и объект, к которому следует применить стиль.
GeoGebra 6.0.580.0 Classic + Portable (x86-x64) (2020) =Multi/Rus=
Версия программы:
6.0.580.0 Classic
Официальный сайт:
www.geogebra.org
Язык интерфейса:
Русский, Английский и другие.
Лечение:
не требуется
Системные требования:
• Windows XP — Windows 10 (x32/x64) • Виртуальная среда Java.
Описание:
GeoGebra — мультиплатформенное программное обеспечение для математиков, распространяемое авторами бесплатно, позволяющее открыть новые горизонты понимания геометрии и алгебры, визуализировать сложные выражения, научиться в интерактивной форме понимать, как происходит построение сложных геометрических фигур. Такой симбиоз нескольких наук в едином интерфейсе приложения, позволит намного быстрее освоить множество приемов в системе координат, понимание правильно построения геометрических фигур не только на плоскости, но и в пространстве. Особенная ценность данное ПО, состоит в том, что ученики средних школ и студенты, смогут в интересной, не стандартной форме получить дополнительные знания, упражняясь и развиваясь самостоятельно.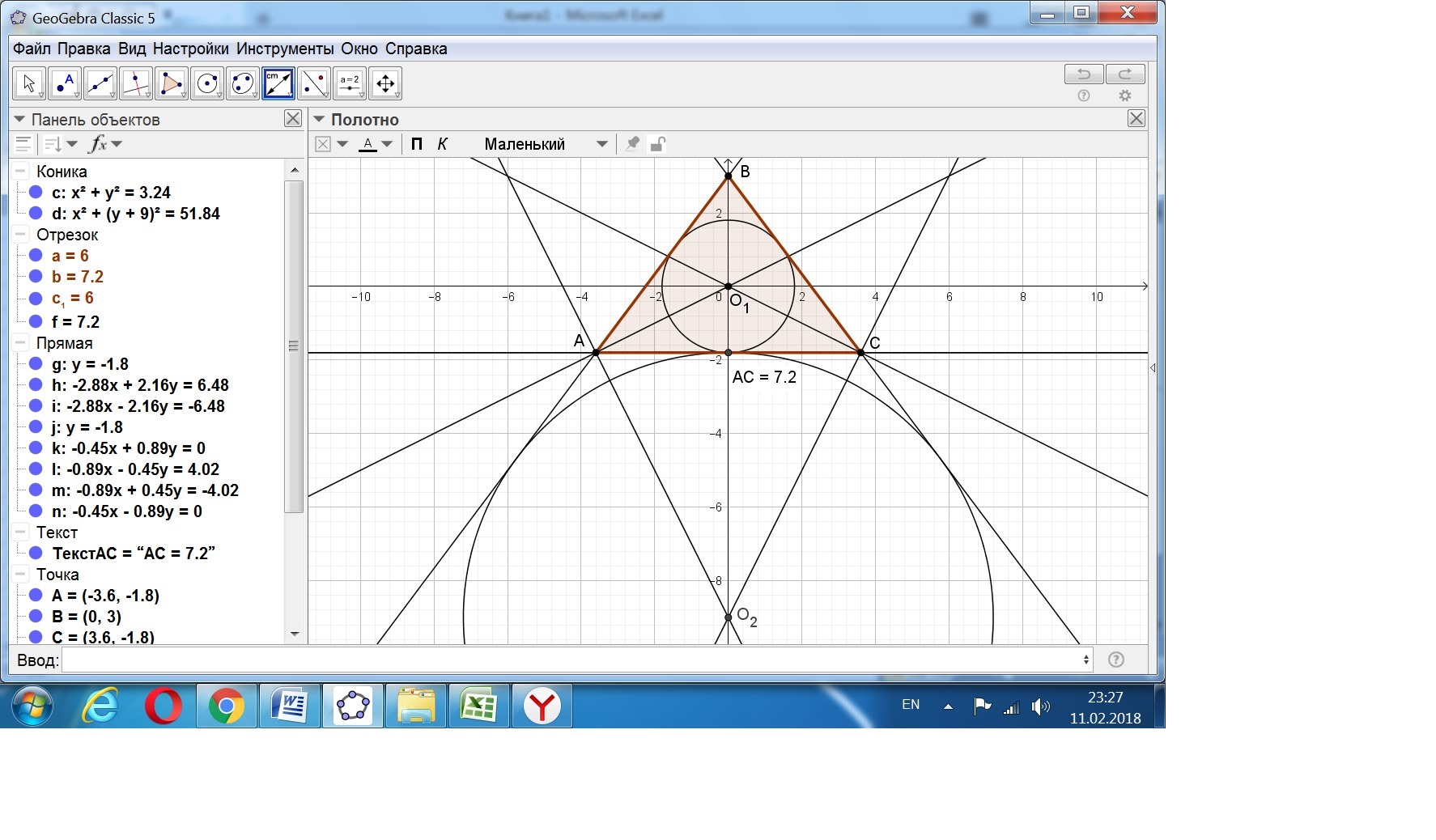 Основные понятия, полученные таким образом станут возможно крепким фундаментом при дальнейшем обучении и возможно даже открытий.
Основные понятия, полученные таким образом станут возможно крепким фундаментом при дальнейшем обучении и возможно даже открытий.
«Основные возможности:»
• Построение кривых • Построение графиков функций; • Построение кривых, заданных параметрически в декартовой системе координат:; • Построение конических сечений: Коника произвольного вида — по пяти точкам. • Окружность: — по центру и точке на ней; — по центру и радиусу; — по трем точкам; • Эллипс — по двум Фокусам и точке на кривой; • Парабола — по фокусу и директрисе; • Гипербола — по двум фокусам и точке на кривой; • 3D моделирование • Построение геометрического места точек, зависящих от положения некоторой другой точки, принадлежащей какой-либо кривой или многоугольнику (инструмент Локус). • Вычисления • Действия с матрицами: сложение, умножение; • Транспонирование, инвертирование; • Вычисление определителя; • Вычисления с комплексными числами; • Нахождение точек пересечения кривых; • Статистические функции: вычисление математического ожидания, дисперсии; • Вычисление коэффициента корреляции; • Аппроксимация множества точек кривой заданного вида: полином, экспонента, логарифм, синусоида • Работа с таблицами • Анимация • Много новых команд, например SlopeField, LocusEquation, SurdText • Новые и улучшенные инструменты: Перо, Freehand Формы, Удаление, Жесткий Полигон • Программа позволяет создавать Java-апплеты динамических чертежей для их включения в Веб-страницы • Загрузка готовых шаблонов с официального сайта в формате . ggb • И многое другое …
ggb • И многое другое …
«Материалы для обучения:»
Множество бесплатных доп. материалов
«Что нового:»
Release Notes GeoGebra
«O portable:»
Программа от разработчиков, не требует инсталляции и предустановленной среды Java. Запускается и работает с любого USB носителя. Раздается в виде авторских архивов по причине высокого сжатия архива с контрольными суммами: GeoGebra-Windows-Portable-6-0-580-0
CRC32: 43A2A16E MD5: A6D3B5719B98D22ED897BB457FCBF736 SHA-1: 574565FCE474BD81B0AA12108A00F04701D670CD
Скриншоты:
NIT for You | Geogebra
GeoGebra (Геогебра) — это динамическая математическая программа, которая объединяет геометрию, алгебру и исчисления. Она разработана для изучения и преподавания математики в школах Маркусом Гогенвартером (Markus Hohenwarter) и международым сообществом программистов
Видео — урок 1
Видео — урок 2
youtube.com/embed/z3cVYYup-KY» frameborder=»0″ allowfullscreen=»allowfullscreen»/>
Интерфейс
Главное окно разделено на Виды. По умолчанию слева расположена Панель объектов, а справа — Полотно. Над ними могут быть размещены Панель меню и Панель инструментов, а под ними — Шаги построения. Многие функции могут быть доступны с помощь горячих клавиш. Программа также включает специальные возможности, такие как Клавиатура.
Что такое инструменты?
Задание: Построить окружность, используя инструмент Окружность по центру и точке.
- Выберете инструмент Окружность по центру и точке.
- Щёлкните два раза в Поле чертежа для создания окружности. Замечание: Первый щелчёк задаёт цент окружности, а второй — её радиус.
- Выберете инструмент Перемещение и передвиньте точки, чтобы изменить размер и/или положение окружности.
- Найдите Набор инструментов для инструмента Отрезок.

- Щёлкните два раза в Поле чертежа чтобы создать две точки и отрезок между ними.
- Выберете инструмент Перемещение и передвиньте точки, чтобы изменить размер и/или положение отрезка.
Подсказка: если вы хотите узнать об инструменте побольше, щёлкните по Подсказке. Откроется страница с более детальной информацией о выбранном Инструменте.
Задание: Выяснить, как работает инструмент Многоугольник, и создать произвольный треугольник.
- Выберите инструмент Многоугольник.
- Прочитайте Подсказку.
- Выясните, как использовать этот инструмент, чтобы создать треугольник.
Закончив чертёж, вы можете:
- сохранить его в файл (формат файла GeoGebra),
- создать Интерактивный чертеж с помощью аплета Java или HTML5,
- распечатать чертёж, в том числе и с протоколом,
- Экспортировать в изображение в форматах PNG, SVG, PDF, EPS, EMF или LaTeX и Asymptote,
- загрузить на сайт.

Режим онлайн
Примеры
Ресурсы:
Использование возможностей сервиса GeoGebra. Org при обучении математике Текст научной статьи по специальности «Науки об образовании»
Ушакова М.А., к.п.н., доцент Филиал РГППУ в г. Нижний Тагил Неустроева А.В.,
студентка 4 курса, гр.41ФМО филиала РГППУ в г. Н. Тагиле г. Нижний Тагил, Россия
ИСПОЛЬЗОВАНИЕ ВОЗМОЖНОСТЕЙ СЕРВИСА GEOGEBRA.ORG ПРИ ОБУЧЕНИИ МАТЕМАТИКЕ
Аннотация
В данной статье говорится о необходимости образования шагать в ногу со временем, а именно внедрять в процесс обучения информационно-коммуникативные технологии. Внедрение такой технологии можно осуществить, например, через применение на уроке разнообразных сервисов. В статье рассмотрены варианты применения сервиса Geogebra. org, дана его краткая характеристика и приведено несколько упражнений.
org, дана его краткая характеристика и приведено несколько упражнений.
Ключевые слова: Geogebra.org, сервис, интернет, математика, информационно-коммуникативные технологии.
Ushakova M. A.,
Ph. D., associate Professor Branch rgppu in Nizhny Tagil Neustroeva, A. V., 4th year student, gr.41ФМО branch rgppu in N. Tagil Nizhny Tagil, Russia
THE USE OF SERVICE CAPABILITIES GEOGEBRA.ORG WHEN
TEACHING MATH
Abstract
In this article it is spoken about the need for education to keep pace with the times, namely, to introduce into the learning process of information and communication technology. The introduction of this technology can be realized, for example, through the application of the lesson offer a variety of services. The article considers the variants of application of service Geogebra.org, given his brief and given some exercise.
The article considers the variants of application of service Geogebra.org, given his brief and given some exercise.
Key words: Geogebra.org service, Internet, mathematics, information and communication technology.
XXI век вполне правомерно называют эрой знаний и информации. Как нам известно, информационной системой связи является интернет, а мы живем в то время, где он играет огромную роль в нашем существовании. С появлением глобальной сети, люди приобрели возможность обращения к разнообразной информации из любой точки планеты. Благодаря интернету мы имеем доступ к широкому перечню информационных ресурсов (электронные библиотеки, базы данных, архивы и пр.) [3].
С каждым днем информационно-коммуникационные технологии становятся более значимыми во всех сферах человеческой деятельности, особенно в образовании. Это обуславливается тем что, во-первых, образование должно шагать в ногу со временем, а во-вторых, информационно-коммуникативные технологии являются актуальным средством обучения [2]. Именно поэтому, необходимо знакомить студентов — будущих учителей с различными интернет ресурсами, которыми в дальнейшем они могут воспользоваться в своей профессиональной деятельности. Изучение школьной программы с помощью новых технологий будет вызывать у детей интерес к заданию, а, следовательно, и к предмету. Нужно стараться «отходить» от обыденности, от стандартного планирования учебного времени, и приходить к новаторству, к тому, к чему ребенок больше расположен, а современное поколение — это поколение одаренных детей, которые с малых лет достаточно просто и естественно адаптируются к использованию интернета и новых технологий.
Именно поэтому, необходимо знакомить студентов — будущих учителей с различными интернет ресурсами, которыми в дальнейшем они могут воспользоваться в своей профессиональной деятельности. Изучение школьной программы с помощью новых технологий будет вызывать у детей интерес к заданию, а, следовательно, и к предмету. Нужно стараться «отходить» от обыденности, от стандартного планирования учебного времени, и приходить к новаторству, к тому, к чему ребенок больше расположен, а современное поколение — это поколение одаренных детей, которые с малых лет достаточно просто и естественно адаптируются к использованию интернета и новых технологий.
Ни для кого не секрет, что математика — сложный предмет, который нужно не зазубрить, а понять. Чтобы разобраться во всех тонкостях изучаемой науки, необходимо затратить большое количество времени и проявлять скрупулезность. Поэтому возникает вопрос «Как сделать процесс обучения более разнообразным, интересным и, конечно же, результативным?» [5].
Существует множество сервисов, которые являются помощником учителя в быстроте создания заданий, экономии времени, автоматической проверке упражнений. Мы рассмотрим варианты применения сервиса Geogebra.org.
Geogebra.org является веб-приложением, которое завоевало несколько образовательных наград в Европе и США. Geogebra.org позволяет организовать поддержку обучения и процесс преподавания в учебных заведениях различных типов (школа и вуз). Сервис представляет собой бесплатную математическую программу, обладающую множеством возможностей в области геометрии, алгебры, различных вычислений. Он позволяет строить графики, чертежи, кривые, выполнять действия с матрицами, комплексными числами, работать с таблицами и многое другое.
Краткие характеристики Geogebra.org:
• графика, алгебра и таблицы связаны между собой и полностью динамичны;
• легкий в использовании интерфейс, обладает мощными возможностями;
• имеется возможность самим создать интерактивный обучающий материал;
• доступна на многих языках для миллионов пользователей по всему миру;
• бесплатная программа с открытым кодом, официальный сайт программы — www. geogebra.org.
geogebra.org.
Работать с программой очень удобно. Графики строятся с помощью мыши простым перемещением указателя или расстановкой необходимых точек. Все опорные точки добавляются в список в левой части окна программы. Любую точку можно отредактировать как с клавиатуры, так и перемещая ее мышью. Каждый объект можно настроить по своему желанию. Можно изменить цвета, метку, толщину, задать условия отображения, задать действия при клике на объект [1].
Идея использования Geogebra.org заключается в том, что его можно применять как на уроках, так и самостоятельно, проверяя и закрепляя свои знания в нестандартной (игровой) форме. Именно это и позволяет формировать познавательный интерес.
Для примера рассмотрим упражнение «Дорисуй смайлик». Чтобы дорисовать смайлик, нужно при помощи ползунков верно выставить значения абсцисс и ординат точек А, В, С, D и Е. (рис. 1).
(рис. 1).
Дорисуй смайлик
ЧтоОн дччкомт* смлйлм. ц>м ¡чж псион»« оипумни мрюпктми!* ***** абсцисс * т«м*: Л, I
Y
V
V
л. ■ — • 1
© S
При помощи ползунков
установи координаты точек, чтобы дорисовать смайлик.
Дорисуй смайлик
•+ПЙ»« ДВр*вМТЪ € ШиЛЩ. «ум« при П4**ВД11WIÏVW» вмсгд
Я ЦвСфСС (I чрзми*т «
При помощи ползунков установи координаты точек, чтобы дорисовать смайлик. ч жзпэумсе кдо аыствытъ ««мент -Ухци« иoiïiimi А В С. D н Е
ч жзпэумсе кдо аыствытъ ««мент -Ухци« иoiïiimi А В С. D н Е
Рис.1. Упражнение «Дорисуй смайлик»
Следующее упражнение «Интерактивные углы на тригонометрической окружности». При выполнении этого задания необходимо переместить красную точку на окружности, затем проверить правильность ее позиции.
Рис.2. Упражнение «Интерактивные углы на тригонометрической
окружности»
Не секрет, что сегодня качественная подготовка учащихся невозможна без профессионального мышления со стороны педагога, которое впоследствии позволяет обновлять свои знания, повышать квалификационный уровень, находить новые нестандартные способы решения профессиональных задач и реализовывать их на практике. В современных условиях от учителя требуется не только уметь работать с информацией, логически думать, правильно анализировать реальные процессы и принимать оптимальные решения, но и грамотно конструировать занятия, находя все более интересные и нестандартные решения предъявления сложной для учащихся информации [4].
Таким образом, можно сделать вывод, что сервис Geogebra.org является хорошим помощником учителя математики. Его инструменты будут востребованы при проведении устного счёта, при изучении нового материала, при проверке фронтальных самостоятельных работ и пр.
При правильном использовании интернета процесс обучения становится разнообразнее и интереснее. Различные виды деятельности, которые можно организовать только используя интернет, позволяют мотивировать учащихся сделать то или иное задание, делают процесс обучения для современных школьников более увлекательным.
ЛИТЕРАТУРА
1. Алышова Н. С. Использование программы Geogebra на уроках математики. [Электронный ресурс]. — Режим доступа: http: //www. gramota. net/materials/1/2013/1/5. html.
2. Бритова О. Использование интернет-ресурсов. [Электронный ресурс] Режим доступа: http://www.docme.ru/doc/85695/ispol._zovanie-internet-resursov.
Бритова О. Использование интернет-ресурсов. [Электронный ресурс] Режим доступа: http://www.docme.ru/doc/85695/ispol._zovanie-internet-resursov.
3. Быкова А. А. Применение интернет ресурсов на уроках математики. Интерактивные формы обучения. [Электронный ресурс]. — Режим доступа: http://arinaalekceevna.ucoz.com/publ/primenenie_internet_resursov_na_urokakh_ma tematiki_interaktivnye_formy_obuchenij a/1-1-0-6.
4. Волкова Е.А. Научно-методические подходы к использованию интерактивных средств обучения в подготовке будущих учителей //Научные исследования: от теории к практике. 2015. Т. 1. № 2 (3). С. 174-176.
5. Использование информационно-коммуникационных технологий на уроках математики. [Электронный ресурс]. — Режим доступа: http://videouroki.net/filecom.php?fileid=98697689.
6. Мащенко М. В. Развитие учебной мотивации у младших школьников с помощью ИКТ // Учебные записки ИИО РАО. — М.: Институт информатизации образования 2005. №16. С. 62-65
В. Развитие учебной мотивации у младших школьников с помощью ИКТ // Учебные записки ИИО РАО. — М.: Институт информатизации образования 2005. №16. С. 62-65
Использование программы GeoGebra на уроках математики.
Здравствуйте. Сегодня я хочу с вами поделиться, как использую программу GeoGebra на уроках математики.
GeoGebra — это бесплатная, кроссплатформенная динамическая математическая программа для всех уровней образования, включающая в себя геометрию, алгебру, таблицы, графы, статистику и арифметику, в одном удобном для использования пакете.
Программа бесплатно скачивается с сайта производителя https://www.geogebra.org/download ,устанавливается за несколько минут на компьютер, планшет, смартфон или если хотите можно работать в программе онлайн.
Программа написана Маркусом Хохенвартером на языке Java, а значит, работает на большом числе операционных систем, переведена на 39 языков и в настоящее время активно разрабатывается, на русский язык переведена в 2013 году.
Geogebra позволяет создавать на экране компьютера чертежи, которые можно использовать на разных стадиях изучения учебного материала, от живых плакатов до исследовательских чертежей. Особенно поучителен сам процесс создания соответствующего рисунка.
Интерфейс программы GeoGebra (ГеоГебра) напоминает классную доску, на которой можно рисовать графики, создавать геометрические фигуры и т.п. В окне программы будет наглядно отображены производимые изменения: если вы измените уравнение, кривая перестроится, изменится масштаб или ее положение в пространстве, уравнение, написанное рядом с кривой, автоматически будет скорректировано, согласно новым значениям.
Возможности программы по математике не ограничиваются только построением графиков. Программу GeoGebra можно будет использовать для интерактивных чертежей при решении геометрических задач. Программа GeoGebra обладает мощными и функциональными возможностями, которые позволяет наглядно и просто обучаться математике.
В программе GeoGebra можно создавать различные 2D и 3D фигуры, интерактивные ролики, которые затем можно будет размещать в интернете. Готовые чертежи можно сохранять в виде картинки и вставлять в документ. У программы богатые возможности работы с функциями за счёт команд встроенного языка (который, кстати, позволяет управлять и геометрическими построениями).
Готовые чертежи можно сохранять в виде картинки и вставлять в документ. У программы богатые возможности работы с функциями за счёт команд встроенного языка (который, кстати, позволяет управлять и геометрическими построениями).
Интерфейс GeoGebra
Интерфейс программы GeoGebra напоминает графический редактор. Программу можно использовать для черчения, но это не основное предназначение приложения.
Давайте рассмотрим основные элементы интерфейса программы GeoGebra:
Полоса меню. Из меню вы можете изменить настройки программы.
Панель инструментов. Здесь находятся инструменты для создания объектов. После щелчка по треугольнику в правом нижнем углу кнопки, будут открыты дополнительные инструменты. Операции, доступные в панели инструментов, можно производить с помощью строки ввода.
Панель объектов. В Панели объектов отображаются введенные переменные и функции. Вместо имен переменных здесь отображаются их значения. Для того чтобы увидеть формулу в символьном виде, нужно будет кликнуть по ней правой кнопкой мыши.
Кнопки «Отменить» и «Повторить».
Строка ввода. Это основной инструмент при работе в программе GeoGebra. Здесь вводятся команды и формулы, задаются значения переменных. Справа от строки ввода расположена кнопка «Список команд». С помощью дополнительных команд можно будет вводить команды и отсутствующие на клавиатуре символы.
Рабочая область. Все построения в программе производятся в рабочей области. Вы можете изменить масштаб с помощью колесика мыши, перемещать по рабочей области ось координат.
Рассмотрим примеры применение программы на уроках:
1.Построить развёртку куба (задача 5 класса).
2. Построить развёртку пирамиды.
3.Задание: постройте фигуру по заданным координатам (5,6,7 класс)
«Звёздочка»
(-6;0), (-3;1), (-4;4), (-1;3), (0;6), (1;3), (4;4), (3;1), (6;0), (3;-1), (4;4), (1;3), (0;-6), (-1;-3),
(-4;-4), (-3;1), (-6;0)
4. Постройте график функции:
Постройте график функции:
y= −|4x+3|
Определите, при каких значениях m прямаяy=m имеет с графиком ровно три общие точки.
5. Постройте график функции:
y=
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Построить график функции (11 класс).
8.Рабочая тетрадь по геометрии 10 класс.
Задача №38.
Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки P,F и M- середины ребер АА1, А1В1 и DC. Укажите точку пересечения диагоналиBD1 с секущей плоскостью.
9.Л.С.Атанасян. Геометрия 10-11.
Задача №170. Из вершины B треугольника ABC, сторона AC которого лежит в плоскости α, проведен к этой плоскости перпендикуляр BB1. Найдите расстояния от точки B до прямой AC и до плоскости α, если AB = 2 см, ∟BAC = 150° и двугранный угол BACB1 равен 45°.
Использование программы GeoGebra на уроках позволяет:
— оптимизировать учебный процесс, более рационально используя время на различных этапах урока;
— осуществлять дифференцированный подход в обучении;
— проводить индивидуальную работу, используя персональные компьютеры;
— снизить эмоциональное напряжение на уроке, внося в него элемент игры,
— расширять кругозор учащихся;
— способствует развитию познавательной активности учащихся.
Применение данной программы на уроках математики способствует:
— повышению интереса к изучаемому предмету у слабоуспевающих учащихся;
— повышение уровня самооценки учащихся;
— развитие навыка самоконтроля;
— побуждение к открытию и изучению нового в сфере информационных технологий, желанию поделиться с товарищами своими знаниями.
Считаю, что каждый учитель математики должен попробовать включить в свой арсенал приложение » GeoGebra «.
Интернет ресурсы:
https://www.geogebra.org/download
Литература:
Л.С.Атанасян. Геометрия 10-11.
Рабочая тетрадь по геометрии 10 кл.
Учебники по алгебре А.Г.Мордкович.
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/260133-ispolzovanie-programmy-geogebra-na-urokah-mat
PDST Математика после начального образования | Научитесь использовать GeoGebra
Почему студенты-математики используют GeoGebra?
GeoGebra — это простой, но мощный инструмент, который студенты могут использовать для понимания математических концепций, для помощи в решении задач и проверки решений. GeoGebra может использоваться для статистики, вероятности, геометрии, тригонометрии, алгебры и функций. Вы можете изучить основы GeoGebra очень быстро, и в кратчайшие сроки вы увидите свои математические данные по-новому.
Обучающие программы GeoGebra
Чтобы помочь вам начать работу с GeoGebra, вот несколько коротких видеороликов, которые объясняют основы GeoGebra.
Хотите загрузить и установить GeoGebra? Просто следуйте инструкциям в этом руководстве …
Настроить GeoGebraИз этого туториала Вы узнаете, как изменить некоторые базовые настройки GeoGebra, чтобы упростить его …
Перемещение графического представленияПеремещение и масштабирование графического представления — одна из самых полезных вещей, которые нужно знать в Geo …
Вставка изображенияПри связывании математики с реальной жизнью может быть полезно вставить изображение в GeoGebra….
Введение в геометриюЗнание нескольких основных инструментов упрощает изучение геометрии с помощью Geogebra. Это …
Разделите отрезок пополамХотите построить серединный перпендикуляр к отрезку прямой? Этот учебник будет …
Уравнение окружностиПонять уравнение круга намного проще, когда вы видите круг …
Введение в статистику Используйте GeoGebra с данными Census @ SChool для создания диаграмм, расчета средних значений и стандартной разработки. ..
..
Инструкции по эксплуатации GeoGebra
Что такое GeoGebra?
GeoGebra — это бесплатный пакет программного обеспечения для динамической математики, используемый учителями математики в классах по всему миру. Он объединяет геометрию, алгебру, таблицы, графики, статистику и вычисления в одном удобном пакете. Он выиграл несколько наград в области образовательного программного обеспечения по всему миру.
7 шагов к интерактивной математике с Geogebra: основы
Это начало года, и я так рад, что взял перерыв в публикации.Это дало мне возможность прочитать несколько замечательных книг, поработать над несколькими побочными проектами, о которых вы скоро услышите, привести дом, наконец, в порядок, и провести чудесное время с семьей.Так как я не писал в праздники, я не смог сделать вам подарок. Поэтому, хотя это и запоздало, я хотел поделиться с вами одним из моих любимых бесплатных программ с открытым исходным кодом — Geogebra (Геометрия + Алгебра).
 Я помню, как впервые увидел это программное обеспечение много лет назад и увидел потенциал образовательных технологий.Фактически, в этом году я буду выступать на конференции CUE 2011 г. в Палм-Спрингс под названием «Геогебра для интерактивной математики».
Я помню, как впервые увидел это программное обеспечение много лет назад и увидел потенциал образовательных технологий.Фактически, в этом году я буду выступать на конференции CUE 2011 г. в Палм-Спрингс под названием «Геогебра для интерактивной математики».Стоит ли начинать использовать Geogebra? Хорошо, скажите мне, испытывали ли вы это:
- Сложность построения графиков на доске из-за времени или качества навыков рисования.
- Путаница с вашими учениками по поводу взаимосвязи переменных и их коэффициентов (например, что происходит, когда «m» или «b» изменяются в y = mx + b).
- Студенты забывают длинное доказательство или шаги по решению уравнения.
- И все другие разочарования, связанные с ограничениями реальности для объяснения абстрактных понятий.
Если вы кивнули на что-то из вышеперечисленного, то вам понадобится Geogebra. Не волнуйтесь, это бесплатно и легко начать.
Начало работы с Geogebra
Шаг 2: У вас есть 3 варианта использования Geogebra, чтобы учесть как можно больше возможных ситуаций.
- Webstart — это вариант выбора, если вы хотите использовать Geogebra в автономном режиме.Это требует, чтобы вы установили программное обеспечение, и поэтому обязательно поговорите с ИТ-отделом вашего учебного заведения о настройке. Хороший вариант, если вы можете получить его на случай, если интернет не работает.
- Запуск апплета — Позволяет полностью использовать Geogebra в веб-браузере, пока вы подключены к Интернету.
- Автономная установка — Используйте эту опцию, чтобы загрузить программу установки Geogebra и поделиться ею с учащимся, если у них нет доступа к Интернету .
Шаг 3 : Откройте Geogebra. Он будет выглядеть одинаково независимо от того, как вы его открываете и на каком компьютере, что прекрасно, когда вы работаете со студентами.
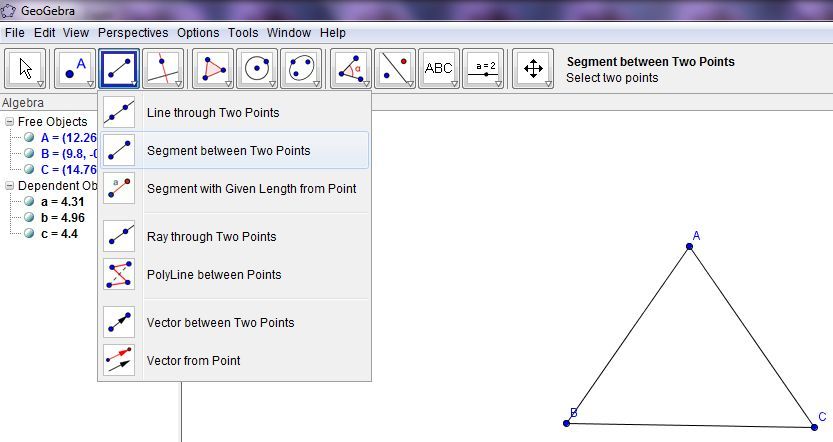
Давайте посмотрим на строительные инструменты, которые вы будете использовать чаще всего. Эти инструменты используются вместе с другими для создания объектов и управления ими.
Эти кнопки также служат для хранения дополнительных инструментов.Я опишу каждую кнопку и дополнительные инструменты в этом меню. Чтобы увидеть дополнительные инструменты, просто нажмите на маленькую стрелку в правом нижнем углу каждой кнопки.
Слева направо вы найдете:
- Перемещение, поворот, запись в электронную таблицу
- Новая точка, пересечение двух объектов, середина или центр
- Инструменты для линий, сегментов, векторов и лучей
- Перпендикулярный, параллельный, касательный, наилучшее соответствие
- Нарисовать многоугольник или правильный многоугольник
- Круглые инструменты
- Эллипс, Гипербола, Парабола
- Угол, расстояние, площадь и наклон
- Размышления и переводы
- Слайдеры, текст, изображения
- Перемещение, масштабирование, отображение / скрытие
Вы заметите, что была создана новая точка, обозначенная буквой «A».Это также отражено слева в разделе «Свободные объекты». Это означает, что вы можете изменить или переместить точку, если хотите.
Теперь создайте еще одну точку в любом месте. Будет создана новая точка с меткой «B», и координаты точек A и B показаны с левой стороны.
Шаг 5: Давайте превратим эти точки в линию. Нажмите кнопку с соответствующим названием «Линия через две точки» справа от кнопки новой точки. Затем щелкните Point A , а затем Point B на графике.Формируется новая линия с надписью «a» (строчная буква, чтобы отличать ее от точек, и вы можете изменить все имена на любые, которые захотите позже).Если вы выполнили предыдущие шаги правильно, вы также должны увидеть уравнение для вашей линии под зависимыми объектами (поскольку оно зависит от Point A и B ). По умолчанию используется стандартная форма (Ax + By = C), но вы можете изменить ее на форму пересечения наклона, щелкнув правой кнопкой мыши по линии и выбрав y = mx + b. Вы можете видеть это на картинке ниже, но помните, что наши точки и линии будут отличаться, поэтому мои числа не совпадают с вашими.
Вы, наверное, в восторге от того, насколько яснее и точнее могут быть ваши математические демонстрации. Позвольте мне показать вам еще пару вещей сегодня, и в следующий раз мы пойдем немного дальше.
Шаг 6: Проведем перпендикулярную линию. Нажмите следующую кнопку справа под названием «Перпендикулярная линия». Он просит вас щелкнуть точку и линию, поэтому щелкните либо Point A , Point B , либо создайте Point C с помощью кнопки добавления новой точки из шага 4.Затем щелкните Line A . Ваша перпендикулярная линия создана. Если вы хотите «отменить» шаг, нажмите Ctrl + Z или выберите его в меню «Правка», но последователи этого блога знают, как эффективно использовать сочетания клавиш.Вам может потребоваться сдвинуть или уменьшить масштаб, и вы можете легко сделать это, нажав кнопку «Переместить графический вид». Просто убедитесь, что вы нажали кнопку «Переместить» (крайняя слева), чтобы снова нажимать на объекты.
Шаг 7: Каким бы удивительным ни был Geogebra, вы можете спросить себя, почему в моей демонстрации CUE Conference упоминается использование Geogebra для создания «Интерактивной математики».Что ж, обычно после того, как вы распечатали рабочий лист или нарисовали что-то на доске, это будет сделано, и поиграть с этим трудно, если не невозможно. Существуют дорогие доски SMART, которые могут создавать интерактивную математику, но вы можете делать это бесплатно с помощью компьютера и Geogebra.
Убедитесь, что кнопка «Переместить» в крайнем левом углу выбрана, выберите, удерживайте и перетащите точку A. Вы должны увидеть всю линию и сдвиг перпендикулярной линии, а также уравнения и точки слева.Посмотрите видео ниже, чтобы увидеть Geogebra в действии.
Довольно круто, да? Математика не должна быть мертвой, теперь студенты могут играть с ней, и играть они будут. Позвольте им расслабиться на Geogebra, и они в кратчайшие сроки создадут удивительные произведения искусства, рисунки и конструкции.
В следующих нескольких статьях я покажу вам еще больше удивительных вещей в Geogebra. Мы должны уметь охватить:
- Слайдеры и анимация
- Встраивание и обмен файлами Geogebra с вашими учениками и всем миром
- И некоторые замечательные ресурсы от других преподавателей, которые вы можете сразу же начать использовать в своем классе.
Подпишитесь на BrokenAirplane!
Безопасность | Стеклянная дверь
Мы получаем подозрительную активность от вас или кого-то, кто пользуется вашей интернет-сетью.Подождите, пока мы подтвердим, что вы настоящий человек. Ваш контент появится в ближайшее время. Если вы продолжаете видеть это сообщение, напишите нам чтобы сообщить нам, что у вас возникли проблемы.
Nous aider à garder Glassdoor sécurisée
Nous avons reçu des activités suspectes venant de quelqu’un utilisant votre réseau internet. Подвеска Veuillez Patient que nous vérifions que vous êtes une vraie personne. Вотре содержание apparaîtra bientôt. Si vous continuez à voir ce message, veuillez envoyer un электронная почта à pour nous informer du désagrément.
Unterstützen Sie uns beim Schutz von Glassdoor
Wir haben einige verdächtige Aktivitäten von Ihnen oder von jemandem, der in ihrem Интернет-Netzwerk angemeldet ist, festgestellt. Bitte warten Sie, während wir überprüfen, ob Sie ein Mensch und kein Bot sind. Ihr Inhalt wird в Kürze angezeigt. Wenn Sie weiterhin diese Meldung erhalten, informieren Sie uns darüber bitte по электронной почте: .
We hebben verdachte activiteiten waargenomen op Glassdoor van iemand of iemand die uw internet netwerk deelt.Een momentje geduld totdat, мы выяснили, что u daadwerkelijk een persoon bent. Uw bijdrage zal spoedig te zien zijn. Als u deze melding blijft zien, электронная почта: om ons te laten weten dat uw проблема zich nog steeds voordoet.
Hemos estado detectando actividad sospechosa tuya o de alguien con quien compare tu red de Internet. Эспера mientras verificamos que eres una persona real. Tu contenido se mostrará en breve. Si Continúas recibiendo este mensaje, envía un correo electrónico a para informarnos de que tienes problemas.
Hemos estado percibiendo actividad sospechosa de ti o de alguien con quien compare tu red de Internet. Эспера mientras verificamos que eres una persona real. Tu contenido se mostrará en breve. Si Continúas recibiendo este mensaje, envía un correo electrónico a para hacernos saber que estás teniendo problemas.
Temos Recebido algumas atividades suspeitas de voiceê ou de alguém que esteja usando a mesma rede. Aguarde enquanto confirmamos que Você é Uma Pessoa de Verdade.Сеу контексто апаресера эм бреве. Caso продолжить Recebendo esta mensagem, envie um email para пункт нет informar sobre o проблема.
Abbiamo notato alcune attività sospette da parte tua o di una persona che condivide la tua rete Internet. Attendi mentre verifichiamo Che sei una persona reale. Il tuo contenuto verrà visualizzato a breve. Secontini visualizzare questo messaggio, invia un’e-mail all’indirizzo per informarci del проблема.
Пожалуйста, включите куки и перезагрузите страницу.
Это автоматический процесс. Ваш браузер в ближайшее время перенаправит вас на запрошенный контент.
Подождите до 5 секунд…
Перенаправление…
Заводское обозначение: CF-102 / 65cd1c949ce04979.
Использование Geogebra
В этой статье предлагаются советы и подсказки, которые помогут максимально эффективно использовать GeoGebra для решения геометрических задач.
GeoGebra — это программное обеспечение для динамической геометрии с множеством различных функций, и, поскольку оно имеет открытый исходный код, вы можете использовать его бесплатно.Возможно, вы захотите посетить этот веб-сайт и загрузить его, прежде чем читать остальную часть этой статьи. GeoGebra также встроен в различные проблемы на сайте NRICH, так что вы, возможно, уже использовали его, даже не осознавая!
Я часто использую GeoGebra, когда пытаюсь понять новую геометрическую проблему, и в этой статье я хотел бы поделиться некоторыми инструментами, которые я считаю полезными. Начнем очень просто, думая о точках и линиях. Ниже приведен апплет GeoGebra, который вы можете использовать для изучения, если вы еще не загрузили программное обеспечение для себя.
Точки и линии
Чтобы нарисовать точку, щелкните второй значок (с синей буквой A), а затем щелкните страницу, на которой должна быть точка. Координаты вашей точки отображаются на панели алгебры сбоку. Если вы затем нажмете на инструмент перемещения (первый значок со стрелкой), вы можете перемещать точку.
GeoGebra пометит вашу первую точку A, вторую точку B и так далее. Если вы передумали относительно точки, вы можете удалить ее несколькими способами — выберите ее с помощью инструмента перемещения и нажмите «Удалить» или щелкните ее правой кнопкой мыши в графическом окне или на боковой панели алгебры и выберите «Удалить» в меню.
Вы также можете добавить новую точку с помощью панели ввода. Попробуйте ввести P = (0,2) на панели ввода. Новая точка, помеченная буквой P, должна появиться в точке с координатами (0,2).
После того, как вы нарисовали несколько точек, вы можете попробовать нарисовать несколько линий, используя третий значок на панели инструментов. Линия соединяет две точки. Попробуйте щелкнуть по двум точкам выбранным инструментом «Линия» и увидеть, как между ними появится прямая линия. После того, как вы нарисовали линию, ее уравнение появится на боковой панели алгебры.
Иногда бывает полезно нарисовать луч или отрезок линии, а не всю линию.Сегмент линии просто рисует отрезок между двумя выбранными вами точками, а луч начинается с одной точки, проходит через другую точку и продолжается дальше. Попробуй нарисовать все три. Обратите внимание, что когда вы рисуете линейный сегмент, его длина отображается на боковой панели алгебры. Это полезно, если вы хотите узнать длины разных частей вашей диаграммы!
Параллель, перпендикуляр и многоугольники
Теперь мы можем рисовать точки и линии, давайте сделаем это немного интереснее! Апплет ниже имеет два новых элемента на панели инструментов.Первый имеет значок перпендикулярной линии. В меню есть много других специальных строк, которые вы можете построить; пока мы сосредоточимся только на первых двух, перпендикулярной и параллельной линиях.
Нарисуйте линию, а затем нарисуйте любую точку на линии или за ее пределами. Выберите инструмент «Перпендикулярная линия», затем щелкните свою линию и свою точку (в любом порядке). GeoGebra строит линию под прямым углом к вашей первой, проходя через выбранную вами точку! Кстати, если ваша диаграмма начинает немного загромождаться, но вы не хотите ничего удалять, вы всегда можете скрыть объект, щелкнув правой кнопкой мыши и отменив выбор «показать объект», или переключив его на боковой панели алгебры.
После того, как вы попробовали нарисовать перпендикулярные линии, используйте инструмент параллельных линий, чтобы таким же образом нарисовать несколько параллельных линий.
Вы заметили другой новый инструмент? Это инструмент многоугольника, который полезен для рисования наборов отрезков прямых линий, из которых вы хотите образовать многоугольник. Просто выберите точки, которые вы хотите присоединить (или щелкните, чтобы создать новые точки), и когда вы закончите, снова щелкните первую точку, чтобы закрыть многоугольник. Обратите внимание, как площадь многоугольника отображается на боковой панели алгебры вместе с длиной каждого сегмент.Перемещайте точки и наблюдайте, как изменяется область …
Если вы хотите нарисовать правильный многоугольник, выберите второй инструмент в меню многоугольника. На этот раз вам понадобится только одна длина стороны, чтобы указать многоугольник вместе с количеством сторон. Итак, выберите первые две точки, чтобы сформировать сторону, а затем введите желаемое количество сторон. Попробуйте нарисовать равносторонний треугольник, квадрат, правильный пятиугольник …
Вы могли заметить, что когда вы рисуете правильный многоугольник, некоторые вершины синие, а некоторые черные! Это потому, что в GeoGebra одни точки и линии зависят от других.Когда вы рисуете точку, она отображается синим цветом, и вы можете перемещать ее с помощью инструмента «Перемещение». Но точку, которая зависит от другого, нельзя поднять и переместить, она движется только вместе с объектом, от которого зависит. Эти точки выглядят как чернить.
Вы также можете нарисовать точку, которая должна находиться на линии или в объекте, используя инструмент «Точка на объекте» на панели инструментов «Точки». Попробуйте построить точку внутри одного из ваших многоугольников. Когда вы пытаетесь переместить его за пределы формы, он останавливается на границе! Эти точки отображаются бледно-голубым цветом, чтобы показать, что они частично ограничены, но все еще могут быть перемещены.
Круги, измерения и преобразования
Когда мы создаем геометрию с помощью бумаги и карандаша, мы не просто используем прямые линии, у нас также есть циркуль, чтобы мы могли рисовать круги и дуги. В приведенном ниже апплете есть несколько дополнительных панелей инструментов. Попробуй нарисовать круг. Есть несколько вариантов: вы можете выбрать центр и точку на окружности, или вы можете выбрать центр, а затем указать радиус, или вы можете выбрать три точки на длина окружности. Вы также можете просто нарисовать дугу или сектор.Почему бы не исследовать с помощью апплета ниже?
После создания диаграммы вы можете узнать о некоторых измерениях. Следующий новый набор инструментов на панели инструментов включает несколько полезных инструментов измерения. Выберите инструмент измерения угла и щелкните две линии или три точки, чтобы измерить угол между ними. Вы можете использовать второй инструмент, чтобы нарисовать угол определенного размера. Также есть инструменты для измерения расстояний и площадей.
Третий новый набор инструментов позволяет выполнять некоторые отражения или вращения.Попробуйте нарисовать многоугольник и линию, а затем отразите ваш многоугольник в этой линии. Просто выберите инструмент отражения, щелкните объект, который хотите отразить, и линию, в которой вы хотите отразить. Изображение автоматически помечается точками, которые соответствуют объекту, поэтому, если ваш объект имеет точку, помеченную буквой A, отраженному изображению соответствует точка A ‘.
Другие инструменты
Это лишь некоторые из инструментов, которые может предложить GeoGebra. Есть много других полезных функций, которые вы можете изучить и узнать о них.
Вот еще несколько функций, которые могут оказаться полезными:
Пересечение — отмечает точки пересечения двух объектов.
Середина / Центр — отмечает середину отрезка линии или центр круга.
Серединный перпендикуляр — рисует серединный перпендикуляр к отрезку прямой.
Биссектриса угла — рисует биссектрису угла.
Касательные — рисует касательную (и) к окружности, проходящей через заданную точку.
Ползунки — это объекты, которые определяют значение в диапазоне, чтобы вы могли создать диаграмму, которая изменяется в соответствии со значением, выбранным на ползунке.
Задачи
Теперь, когда вы познакомились с основными инструментами GeoGebra, вот несколько задач, которые стоит попробовать:
a) Нарисуйте круг и создайте четырехугольник, все точки которого лежат на окружности.
б) Нарисуйте квадрат с равносторонним треугольником на каждой из четырех сторон.
c) Нарисуйте прямоугольный треугольник с квадратами на каждой стороне.
г) Нарисуйте четырехугольник, диагонали которого пересекаются под прямым углом.
д) Нарисуйте прямоугольник, в котором вы можете изменить длину и ширину.
f) Нарисуйте три круга одинакового размера так, чтобы каждый круг проходил через два других центра.
г) Нарисуйте круг и добавьте любую другую точку. Можете ли вы нарисовать круг того же диаметра с другой точкой в качестве центра?
(PDF) ПРИМЕНЕНИЕ GEOGEBRA ДЛЯ ОБУЧЕНИЯ МАТЕМАТИКЕ
Достижения в науке и технологиях Research Journal Vol.8 (24) 2014
52
Развитие и быстрый рост сети Inter-
в сочетании с ее увеличивающейся доступностью для общественности открыли совершенно новый цифровой мир
. Это приводит к тому, что учащиеся в процессе обучения все более склонны принимать
материалов, предоставленных им таким образом. Особенно
по математике, где ряд вопросов требует
большого воображения, ученикам не рекомендуется
изучать предмет, когда он не предоставляется современным и доступным способом
.
Основными препятствиями в обучении математике —
сематике являются:
• Понятия без адекватной иллюстрации,
• Математические графики статичны в классическом способе обучения математике
, т.е. рисовать его
на листе бумаги,
• Статические объекты не позволяют обобщать
концепции.
Национальный совет учителей математики
ematics (NCTM), который является крупнейшим в мире сообществом учителей математики
, объявил технологическую науку
одним из своих шести принципов школьной математики
.
Технологии необходимы в преподавании, а
— в изучении математики; он влияет на математику
, которую преподают, и способствует обучению учащихся
. [3]
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ GEOGEBRA
Основная идея использования GeoGebra в каждый-
дневном обучении и обучении заключается в предоставлении возможности-
связей для студентов с различными математическими навыками
и уровнями для лучшего понимания концепций и
поощряет их к изучению математики новым тяговым способом at-
.
Вот основные характеристики Geogebra:
• бесплатно для некоммерческого использования,
• мультиплатформенность,
• понятный и легкий для понимания графический интерфейс пользователя
,
• богатая база данных готовых примеров,
• техническая документация на многих языках,
• маркировка объектов соответствует математическому синтаксису,
• возможность сохранять проект в нескольких форматах,
• работает с LaTeX,
• все объекты в GeoGebra динамические,
• возможность опубликовать работу на сайте
через javascript,
• программа переведена на многие иностранные языки.
Все это делает GeoGebra отличным инструментом для
преподавания и изучения математики. Поскольку все объекты
в GeoGebra являются динамическими, студенты могут видеть
, как они меняются, когда он изменяет параметры
задачи. В геометрических конструкциях все
объекты, такие как точки, сечения, окружности и
линий, можно перемещать любым способом. Это делает более понятными конструкции
. Кроме того, все построения могут быть выполнены с помощью технологии «наведи и щелкни» или введя их через командную строку.
ИНТЕРФЕЙС
GeoGebra имеет очень четкий и интуитивно понятный интерфейс, разделенный на части, соответствующие алгебре и геометрии
(Рисунок 1). В зависимости от ваших потребностей
может быть свободно модифицирован в соответствии с рассматриваемой проблемой
.
У нас есть несколько представлений:
• алгебраическое представление,
• геометрическое представление,
• представление электронной таблицы,
• представление CAS (система компьютерной алгебры),
• представление проекта протокола,
• командная строка.
Все эти представления связаны друг с другом, то есть
, если мы введем объект в одно из представлений,
он появится в других в соответствующей форме. Так, например,
, если мы поместим функцию в строку команды
, ее график появится в геометрическом виде. Все
изменения параметров функции немедленно отображаются на графике.
Помимо основных возможностей GeoGebra
, таких как рисование рисунков, линий и графиков функций, мы
можем также рассчитывать или измерять углы, точки входа
вырезов, длины, поля, окружности, максимум
мм и минимум функции, производные и
интегралов.Очевидно, что GeoGebra можно использовать как расширенный калькулятор
, но не только. Он может оперировать
векторами, матрицами и даже решать систему из
линейных уравнений.
ПРИМЕРЫ
Мы покажем возможности GeoGebra на
некоторых примерах.
Пример 1
Предположим, мы хотим построить круг, описанный на треугольнике
(рис. 2). Мы знаем, что БЕСПЛАТНЫЕ онлайн-ресурсы по математике
Desmos и GeoGebra!
Ваши ученики изо всех сил пытаются понять концепции в классе?
Вам сложно придумать урок, который поможет студенту открыть для себя концепцию стандартов?
Вы хотите показать учащимся некоторые из концепций построения графиков или геометрии, но ручка и бумага не работают?
Вы можете обратиться за помощью в интерактивном режиме с помощью двух программ для работы с математикой и построения графиков.И они БЕСПЛАТНЫ!
Desmos
Desmos — это онлайн-калькулятор , имитатор графиков, геометрический симулятор и программа уроков , в которой есть несколько хороших материалов, написанных хорошими людьми (включая их главного академического директора Дэна Мейера!). Вы можете поиграть в нее, перейдя на Desmos.com, или взять несколько примеров того, как использовать различные аспекты программы, на Learn.Desmos.com. Вы даже можете создать класс в программе, зайдя на Teacher.Desmos.com, и ваши ученики присоединятся, перейдя на Студент.Desmos.com. У него есть приложение, которое можно загрузить через Apple Store или Google Play для использования на планшетах или телефонах с этими системами.
Первым в списке Desmos числится калькулятор , который можно использовать как простую функцию четырех (+ — x ÷) или в научном режиме с большим количеством функций. Хотя это не симулятор калькулятора TI-30XS Multiview, который мы можем использовать на GED, он близок к этому (, а не , имеет режим mathtype, ). Если вы хотите, чтобы учащиеся видели расчет, и у вас есть проектор или Smartboard, это может быть вам в помощь.Прыгайте и попробуйте.
Где Desmos действительно демонстрирует свою мощь, так это в режиме графического калькулятора . Вы можете начать это, нажав большую красную кнопку НАЧАТЬ ГРАФИК на домашней странице Desmos. Это даст вам рамку ввода и координатную сетку.
- Когда вы вводите точки или формулы во фрейме ввода, объекты появляются в плоскости координатного графика.
- Вы можете щелкнуть символ в рамке ввода, чтобы показать или скрыть объект, и вы можете скрыть или показать метку.
- Серые точки на функции показывают точку пересечения оси Y и корень (и) функции.
- Щелчок по объекту даст вам координатные точки на этом объекте.
- Вы можете увеличивать или уменьшать масштаб с помощью клавиш + или — с правой стороны и можете перетаскивать плоскость, щелкая и перетаскивая место, которое не находится на объекте.
Некоторые действительно полезные вещи, которые мне нравятся, — это ввод формулы с переменными коэффициентами (кроме x или y), ввод формулы с неравенством и построение графиков двух объектов на одной координатной сетке (системы уравнений). Ввод переменных дает вам возможность создать ползунок для настройки значений переменной. Это позволяет вашим ученикам увидеть, как изменение коэффициента или константы меняет график. Ввод неравенства показывает учащимся, как набор решений включает целые области со сплошной или пунктирной границей. Построение системы уравнений позволяет учащимся найти точку (точки) пересечения, решение (я) системы.
Desmos также имеет классную комнату , которую вы можете настроить, чтобы студенты могли работать с стандартными мероприятиями .Перейдите на Teacher.Desmos.com, создайте себе имя пользователя / пароль (опять же, это бесплатно!) И просмотрите уже созданные задания. Если вы выберете занятие для своих учеников, вы получите код, позволяющий студентам присоединиться к занятию на Student.Desmos.com. Есть даже группы действий, связанных вместе. Хотите обсудить функции? Попробуйте набор функций.
GeoGebra
GeoGebra.org — еще одна программа, которая выполняет те же действия ( расчет, построение графиков, геометрия ).Пара различий между ними заключается в том, что GeoGebra также позволяет создавать 3D-графики и имеет приложение, которое можно загрузить на ПК, а также на другие устройства, используемые без подключения к Интернету.
GeoGebra также предлагает занятия, которыми могут заниматься студенты, но больше из занятий всего класса , а не отдельных занятий. На GeoGebra.org/materials вы можете просмотреть ресурсы, созданные учителями для начальной, средней и старшей школы, а также на уровне колледжа. Имейте в виду, что некоторые материалы созданы учителями со всего мира и могут быть на других языках, кроме английского.
Эти две программы предлагают отличные возможности для вас и ваших учеников поиграть с математическими понятиями. Это может создать среду, способствующую GED и подготовке к колледжу в соответствии со стандартами CCRS. Заходите, поиграйте и найдите свое следующее отличное занятие!
Первоначально опубликовано 03.12.18
Изучение математики с помощью GeoGebra — Математика для преподавания
GeoGebra — отличное программное обеспечение для преподавания и изучения математики.Он предлагает инструменты геометрии, алгебры и исчисления в одной среде, действительно отличную поддержку для связывания математических понятий. Кроме того, это бесплатное программное обеспечение с открытым кодом. Щелкните здесь, чтобы загрузить последнюю версию программного обеспечения.
Насколько легко использовать? Да и нет. Да, для учителей математики, потому что они знают математику и поэтому могут легко понять идеи и логику, лежащие в основе инструментов. Да, для студентов, которые были проинструктированы о том, как использовать инструменты и понять математику и логику, лежащие в основе этого.Они могут использовать его при решении задач и для исследования математических соотношений. Но для большинства студентов, особенно тех, кто не изучил основы построения графиков, уравнений и геометрических соотношений, использование GeoGebra ограничивается манипулированием готовыми апплетами GeoGebra. (Щелкните здесь, чтобы увидеть мои сообщения о решении задач о четырехугольниках, или здесь, чтобы познакомиться с функциями с помощью апплетов Geogebra.) Ну да, апплеты GeoGebra просты в использовании, но в большинстве случаев, если вы не знаете математику, лежащую в основе построения конструируй сам, тогда изучение математики может быть поверхностным.
Построение математических моделей с помощью программного обеспечения недоступно для многих младших школьников, которые только начинают изучать основы алгебры и геометрии. Чтобы построить модель, они должны будут следовать установленной процедуре (построенной учителем), не понимая, почему они делают то, что делают. Поэтому я подумал, почему бы не обучать инструментам GeoGebra и математике одновременно? Это задача, которую я поставил перед собой, и я понятия не имею, сработает она или нет. Я подумываю провести исследование позже в этом году.GeoGebra бесплатна и верна математике, поэтому для таких стран, как мы, которые не могут позволить себе покупать лицензионное программное обеспечение, мы получаем такой же качественный обучающий инструмент с Geogebra.



 Для создания геометрических фигур, рисования.
Для создания геометрических фигур, рисования.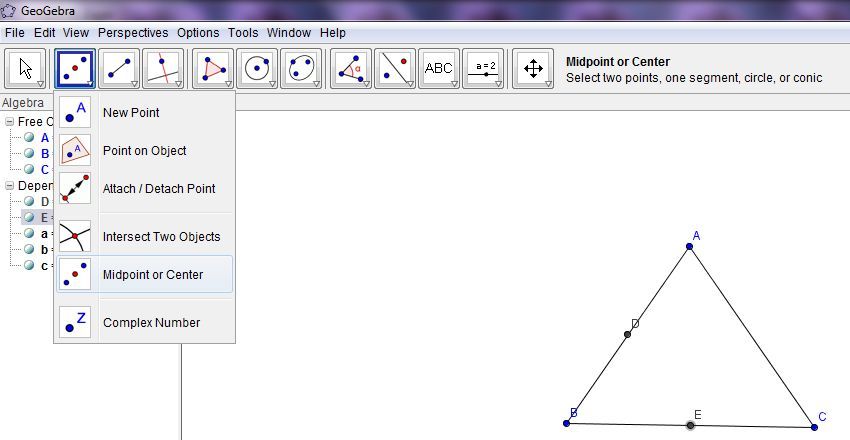 Томск, 2010, C. 168-170 (PDF, 10.2 Mb).
Томск, 2010, C. 168-170 (PDF, 10.2 Mb).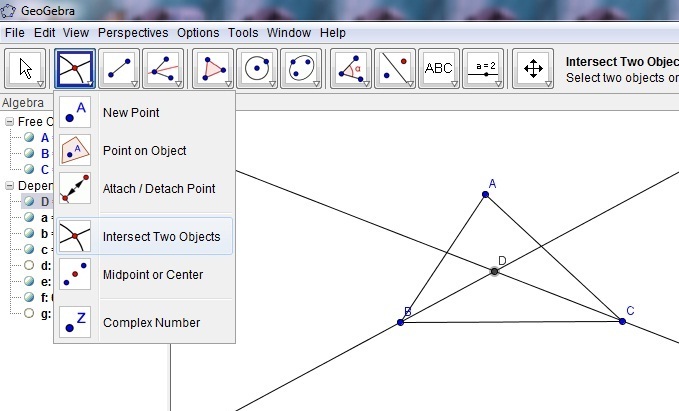 European Journal of Contemporary Education 4(2), 68-71 (PDF, 311 Kb).
European Journal of Contemporary Education 4(2), 68-71 (PDF, 311 Kb).
