Решение больших примеров онлайн: Калькулятор онлайн со скобками

29.05.1970 alexxlab

Содержание

∫ Решение интегралов онлайн с подробным решением

Калькулятор решает интегралы c описанием действий ПОДРОБНО на русском языке и бесплатно!

Это онлайн сервис в один шаг:

Ввести подинтегральное выражение (подинтегральную функцию)

Перейти: Онлайн сервис «Неопределенный интеграл» →

Это онлайн сервис в один шаг:

Ввести подинтегральное выражение (подинтегральную функцию)
Ввести нижний предел для интеграла
Ввести верхний предел для интеграла

Перейти: Онлайн сервис «Определенный интеграл» →

Ввести подинтегральное выражение (подинтегральную функцию)
Введите верхнюю область интегрирования (или + бесконечность)
Ввести нижнюю область интегрирования (или — бесконечность)

Перейти: Онлайн сервис «Несобственный интеграл» →

Ввести подинтегральное выражение (подинтегральную функцию)

Ввести нижний и верхний пределы для первой области интегрирования
Ввести нижний и верхний предел для второй области интегрирования

Перейти: Онлайн сервис «Двойной интеграл» →

Ввести подинтегральное выражение (подинтегральную функцию)
Ввести нижний и верхний пределы для первой области интегрирования
Ввести нижний и верхний предел для второй области интегрирования
Ввести нижний и верхний предел для третьей области интегрирования

Перейти: Онлайн сервис «Тройной интеграл» →

Данный сервис позволяет проверить свои

вычисления на правильность

Возможности

Таблица интегралов

Вы также можете воспользоваться таблицей интегралов, чтобы самостоятельно посчитать любой интеграл, перейти:

Очень продвинутый онлайн калькулятор

Как Вы, наши уважаемые читатели и читательницы, уже могли догадаться, речь пойдет об онлайн калькуляторах, если быть точнее — об одном из самых полезных и, частенько, незаменимых изобретений человека, которое не так давно перекочевало в интернет.

Мы долго выбирали роль самого классного, удобного и полезного онлайн калькулятора и выбор пал на молодой вебдванольный сервис — Web20calc.

Вы, наверное, уже успели возмутиться относительно важности этой темы? Честно говоря, это Вы зря — калькулятор Windows ему совсем не ровня, а ближайшие соперники — типа eCalc, может и превосходят его в функционале, но стоят от 45 евро за копию и при этом устанавливаются на ПК или нетбук или Iphone, что нам не так и нужно.

Данный онлайн калькулятор может:

Корректно выполнять стандартные математические функции, записанные одной строкой типа — 12*3-(7/2) и может обрабатывать числа больше, чемМы даже не знаем, как такое число назвать правильно (тут 34 знака и это совсем не предел). Выводится, к сожалению такое число в файл изображения (защита от автоматического использования скорее всего).
Кроме тангенса, косинуса, синуса и других стандартных функций — калькулятор поддерживает операции по расчёту арктангенса, арккотангенса и прочих.
Доступны в арсенале логарифмы, факториалы и другие интересные функции

Но самое главное — данный онлайн калькулятор умеет строить графики!!! Если не верите, смотрим на скриншот:

Для построения графиков, сервис использует специальную кнопку (график серый нарисован) или буквенное представление этой функции (Plot).

Чтобы построить график в онлайн калькуляторе, достаточно записать функцию, например такую как у нас в скриншоте:

plot(tan(x)),x=-360..360

Мы взяли самый простой график для тангенса, и после запятой указали диапазон переменной X от -360 до 360.

Построить можно абсолютно любую функцию, с любым количеством переменных, например такую:

plot(cos(x)/3z, x=-180..360,z=4) или ещё более сложную, какую сможете придумать.

Обращаем внимание на поведение переменной X — указан промежуток от и до с помощью двух точек.
Единственный минус (хотя трудно назвать это минусом) этого онлайн калькулятора это то, что он не умеет строить сферы и другие объёмные фигуры — только плоскость.

Для сравнения с калькулятором Майкрософта, приводим наглядный скриншот

Думаем игра «Найдите N отличий» Вам знакома. Теперь пора подвести некоторые итоги:

С помощью онлайн калькулятора мы можем:

Серьезно облегчить себе жизнь в школе или институте.
Получить профессиональный онлайн калькулятор в бесплатное пользование.
Считать огромные числа на любом компьютере в любой точке планеты.
Строить графики по сложным функциям прямо онлайн.
Не захламлять свой ноутбук приложениями и, тем более, не тратить на них деньги.

Вполне добротный список преимуществ.
Update 21.10.2011: Мы оформили более удобную страницу с примерами для эффективного использования калькулятором — посмотреть. Её можно открыть с любой точки нашего сайта.

Update 02.12.2010: Теперь можно опробовать этот калькулятор в действии прямо у нас в журнале:

UPDATE 09. 04.2011: Функции арктангенса, арксинуса и т.д. запускаются кнопками:
tan^-1, sin^-1 и т.д.
Включить продвинутые функции для решения матриц, построения графиков, дифференциалов и другого можно с помощью специальных клавиш:

Для полной функциональности нужно использовать оригинал, но этот тоже сойдет для быстрых рассчетов.

Технический калькулятор | Онлайн калькулятор (⇒)

Сейчас другие читают

Математический калькулятор. Подробный онлайн калькулятор всех математических операции.

Математический-Калькулятор-Онлайн v.1.0

Калькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, работа с десятичными, извлечение корня, возведение в степень, вычисление процентов и др. операции.

Решение:

С ← ( ) ±

7 8 9 ÷ %

4 5 6 х √

1 2 3 — x²

0 . = + ¹/_x

Как работать с математическим калькулятором

Клавиша	Обозначение	Пояснение
5	цифры 0-9	Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/-
.	точка (запятая)	Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5
+	знак плюс	Сложение чисел (целые, десятичные дроби)
—	знак минус	Вычитание чисел (целые, десятичные дроби)
÷	знак деления	Деление чисел (целые, десятичные дроби)
х	знак умножения	Умножение чисел (целые, десятичные дроби)
√	корень	Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2
x²	возведение в квадрат	Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16
¹/_x	дробь	Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число
%	процент	Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%»
(	открытая скобка	Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10
)	закрытая скобка	Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки
±	плюс минус	Меняет знак на противоположный
=	равно	Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат.
←	удаление символа	Удаляет последний символ
С	сброс	Кнопка сброса. Полностью сбрасывает калькулятор в положение «0»

Алгоритм работы онлайн-калькулятора на примерах

Сложение.

Пример:

Сложение целых натуральных чисел { 5 + 7 = 12 }

Сложение целых натуральных и отрицательных чисел { 5 + (-2) = 3 }

Сложение десятичных дробных чисел { 0,3 + 5,2 = 5,5 }

Вычитание.

Пример:

Вычитание целых натуральных чисел { 7 — 5 = 2 }

Вычитание целых натуральных и отрицательных чисел { 5 — (-2) = 7 }

Вычитание десятичных дробных чисел { 6,5 — 1,2 = 4,3 }

Умножение.

Пример:

Произведение целых натуральных чисел { 3 * 7 = 21 }

Произведение целых натуральных и отрицательных чисел { 5 * (-3) = -15 }

Произведение десятичных дробных чисел { 0,5 * 0,6 = 0,3 }

Деление.

Пример:

Деление целых натуральных чисел { 27 / 3 = 9 }

Деление целых натуральных и отрицательных чисел { 15 / (-3) = -5 }

Деление десятичных дробных чисел { 6,2 / 2 = 3,1 }

Извлечение корня из числа.

Пример:

Извлечение корня из целого числа { корень(9) = 3 }

Извлечение корня из десятичных дробей { корень(2,5) = 1,58 }

Извлечение корня из суммы чисел { корень(56 + 25) = 9 }

Извлечение корня из разницы чисел { корень (32 – 7) = 5 }

Возведение числа в квадрат.

Пример:

Возведение в квадрат целого числа { (3) ² = 9 }

Возведение в квадрат десятичных дробей { (2,2) ² = 4,84 }

Перевод в десятичные дроби.

Пример:

{ 1/3 = 0,33 }

{ ½ = 0,5 }

Вычисление процентов от числа

Пример:

Увеличить на 15% число 230 { 230 + 230 * 0,15 = 264,5 }

Уменьшить на 35% число 510 { 510 – 510 * 0,35 =331,5 }

18% от числа 140 это { 140 * 0,18 = 25,2 }

Калькулятор онлайн

С этим удобным калькулятором вы можете производить элементарные арифметические операции (сложение, вычитание, умножение, деление) с положительными и отрицательными числами. Доступны действия с дробями и процентами. А также можно выполнить возведение в степень, найти корень из числа и вычислить логарифм.

Для всех возможных действий приведены примеры. Если вам нужно больше функций, откройте научный калькулятор.

Арифметические операции

Сложение

Сложение объединяет два числа (слагаемые) в одно (сумму чисел).

2 + 3 =

Вычитание

Вычитание является обратной операцией к сложению. Вычитание находит разность между двумя числами (уменьшаемое число минус вычитаемое).

3 − 2 =

Умножение

Умножение объединяет два числа в одно число – произведение чисел. Два исходных числа называются множимым и множителем.

2 × 3 =

Деление

Деление является обратной операцией к умножению. Деление находит частное от двух чисел (делимого, поделенного на делитель). Деление любого числа на 0 не определено.

4 ÷ 2 =

Действия с дробями

Дробь представляет собой часть целого или, в более общем смысле, любое количество равных частей. Обычная (простая) дробь состоит из числителя, отображаемого над чертой (или перед косой чертой), и ненулевого знаменателя, отображаемого ниже (или после) черты. Действия с дробями производятся так же, как и с целыми числами.

1 ÷ 2 + 1 ÷ 4 =

Десятичные дроби

Десятичная дробь — это дробь, знаменатель которой не указан явно, но понимается как целое число, равное десяти в степени один (10), два (100), три (1000) и так далее.

. 2 + . 0 3 =

Нахождение обратного числа

Обратное число к x, обозначаемое 1/x или x^-1, представляет собой число, которое при умножении на x дает единицу.

2 1/x =

Действия с процентами

Процент — сотая часть (обозначается знаком %), используется для обозначения доли чего-либо по отношению к целому.

Нахождение процента от числа

40 × 5 % =

Увеличение (уменьшение) числа на процент

40 + 5 % =

Возведение в степень

Возведение в степень — математическая операция, записанная как x^y, включающая два числа: основание x и показатель степени (или степень) y. Когда y — положительное целое число, возведение в степень соответствует многократному умножению основания на себя: то есть, x^y — произведение умножения y оснований.

2 x^y 4 =

Возведение числа в квадрат

Выражение x² называется «квадратом x» или «x в квадрате», потому что площадь квадрата с длиной стороны x равна x×x или x².

2 x² =

Возведение числа в куб

Выражение x³ называется «кубом x» или «x в кубе», потому что объем куба с длиной стороны x равен x×x×x или x³.

2 x³ =

Возведение в степень числа 10

Возведение в степень с основанием 10 используется для обозначения больших или малых чисел. Например, 299792458 м/с (скорость света в вакууме в метрах в секунду) можно записать как 2,99792458 × 10⁸ м/с, а затем округлить до 2,998 × 10⁸ м/с.

4 10^x =

Мнимая единица

Мнимая единица i определяется только тем свойством, что её квадрат равен −1.

i x² =

Корень из числа

В математике y-ый корень числа x, где y обычно является положительным целым числом, представляет собой число z, которое при возведении в степень y дает x, где y — степень корня.

16 ^y√x 4 =

Квадратный корень

Квадратный корень числа x — это число z, которое в квадрате становится x.

9 √x =

Кубический корень

Кубический корень числа x — это число z, куб которого является x.

8 ³√x =

Вычисление логарифма

Логарифм заданного числа x является показателем степени, в которую должно быть возведено другое фиксированное число (основание) y, чтобы получить это число x.

log 8 , 2 =

Десятичный логарифм

Десятичным логарифмом является логарифм с основанием 10.

log 100 =

Натуральный логарифм

Натуральный логарифм числа — это его логарифм по основанию число е.

log 3 , e =

Инженерный калькулятор онлайн

Современный уклад жизни требует постоянной динамики. Производя расчеты на калькуляторе, мы заметно экономим свое время, не рискуем в чем-то ошибиться и получаем точный результат. Благодаря изобретению данного устройства, многие люди забыли что такое недостачи и погрешности в расчетах. Однако калькулятор калькулятору рознь, и если примитивные вычислительные функции можно сделать на математической модели, то сложнейшие расчеты возможно совершить только при помощи инженерной. Отныне приобретать данное чудо современной техники не нужно – достаточно обратиться за помощью к нашему инженерному калькулятору онлайн! Программа работает без дополнительной установки – достаточно зайти на электронную страницу и начать действовать.

Функции инженерного калькулятора онлайн

Калькулятор математического типа поможет вам совершить только примитивные расчеты. С его помощью можно сделать то, чему нас учили в начальных классах средней школы:

сложение;
вычитание;
деление;
умножение;
вычитание процентов;
возведение числа в степень;
нахождение корня квадратного.

Инженерный калькулятор онлайн включает в себя все эти и дополнительные функции, которые необходимы для проведения сложных расчетов. Теперь вам не придется тратить дополнительные деньги на покупку этого устройства, ведь сделать вычисления можно на нашем сайте.

Помимо вышеперечисленных, наш универсальный калькулятор поможет вам выполнить такие расчеты:

Нахождение:

синуса угла;
тангенса;
косинуса;
котангенса;
арксинуса;
арктангенса;
арккосинуса;
арккотангенса.

Интерфейс инженерного калькулятора онлайн

Выполнить все вышеперечисленные расчеты достаточно просто. Наш инженерный калькулятор онлайн обладает понятным интерфейсом, а потому работать с ним весьма удобно. По своему виду он полностью имитирует настоящий калькулятор, поэтому долгого изучения функций вам не потребуется. Несмотря на это мы прилагаем подробную инструкцию и описание каждой клавиши.

Пользоваться нашей программой выгодно еще и потому, что расчеты производятся моментально – вам не нужно обновлять страницу сайта, ведь калькулятор работает во флеш-режиме. Ежедневно нашей программой пользуется огромное количество людей. Среди них ученики высших заведений, преподаватели, архитекторы-проектировщики, ученые и другие люди, заинтересованные в точности расчетов. Инженерный калькулятор онлайн не требует скачивания и установки дополнительных плагинов, а потому вы можете начать пользоваться им прямо сейчас!

Онлайн калькулятор. Сложение, вычитание, умножение и деление столбиком.

Калькулятор вычисления суммы, разности, произведения и частного столбиком отобразит все этапы решения примера и даст подробное решение. Калькулятор может сложить, вычесть, умножить и разделить столбиком десятичные дроби и целые числа. Для записи десятичной дроби используйте точку либо запятую (например, 1.

12 или 1,12).

Как складывать столбиком

Для того, чтобы сложит два числа столбиком, необходимо записать большее число над меньшим и выполнить последовательное сложение справа на лево, например, сложим столбиком 345 и 67.

345 + 67 = 412

110
₊345
67

412

1) 5 + 7 = 12; 2 пишем, число 1 запишем над числом 4.
2) 4 + 6 = 10; 10 + 1 = 11; 1 пишем, 1 запишем над числом 3.
3) Под числом 3 нет слагаемого, поэтому просто прибавим 3 + 1 = 4
Получилось 412

Приведем еще один пример: 1567 + 761

1567 + 761 = 2328

1100
₊1567
761

2328

1) 7 + 1 = 8, запишем 8.
2) 6 + 6 = 12; 2 пишем, 1 запишем над числом 5.
3) 5 + 7 = 12; 12 + 1 = 13; 3 пишем, 1 запишем над числом 1.
4) Под числом 1 нет слагаемого, поэтому просто прибавим 1 + 1 = 2

Как складывать столбиком десятичные дроби

Для того, чтобы сложить две десятичные дроби, необходимо записать одну десятичную дробь над другой, совместив их точки. Приведем пример: 123.345 + 46.02

123.345 + 46.02 = 169.365

₊123.345
46.020

169.365

1) Запишем число 123.345 над числом 46.02
2) Под числом 5 нет слагаемого, поэтому просто запишем его внизу.
2) Далее сложим 2 и 4; 2 + 4 = 6; запишем 6 внизу.
3) 3 + 0 = 3; записываем 3.
4) Ставим точку
5) 3 + 6 = 9; записываем 9 внизу.
6) 2 + 4 = 6; записываем 6 внизу.
7) Так как под числом 1 нет слагаемого, просто сносим его вниз. Запишем число 1 внизу.
Итак, у нас получилось 169.365

Приведем следующий пример: 123.99 + 12.99

123.99 + 12.99 = 136.98

001010
₊123.99
12.99

136.98

1) 9 + 9 = 18; 8 пишем, 1 запишем над числом 9.
2) 9 + 9 = 18; 18 + 1 = 19; 9 пишем, 1 запишем над числом 3.
3) Ставим точку.
4) 2 + 3 = 5; 5 + 1 = 6; 6 запишем внизу
5) 2 + 1 = 3; 3 запишем внизу.
6) Так как под числом 1 нет слагаемого, просто сносим его вниз.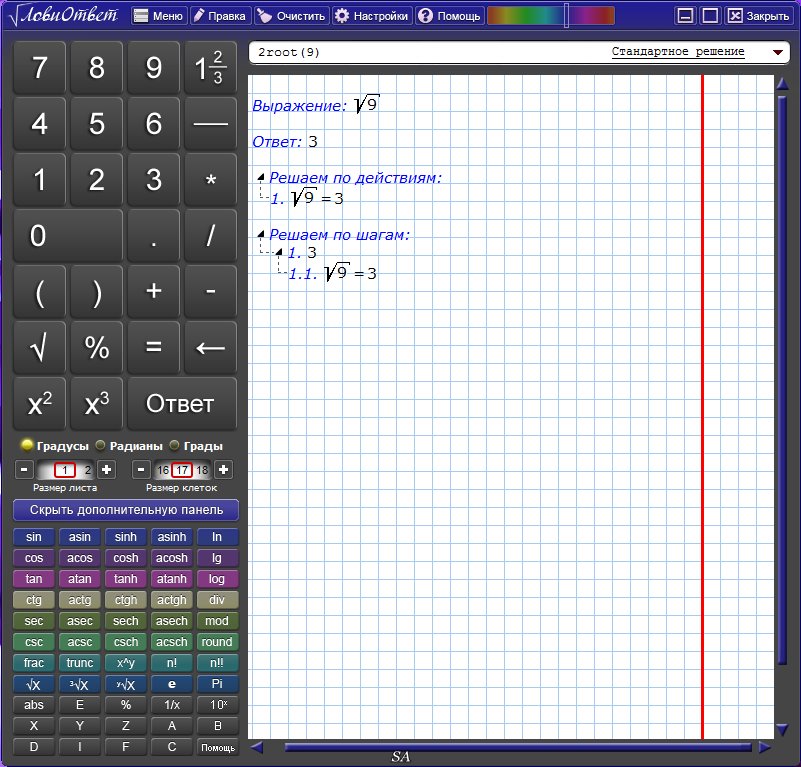 Запишем число 1 внизу.
Ответ: 136.98

Для того чтобы сложить десятичную дробь с целым числом, необходимо сложить целую часть десятичной дроби с целым числом. Сложим, например, 23 и 0.34. У числа 23, после точки поставим столько нолей, сколько чисел после точки у десятичной дроби.

23 + 0.34 = 23.34

₊23.00
0.34

23.34

1) 0 + 4 = 4. Запишем 4.
2) 0 + 3 = 3. Запишем 3.
3) Ставим точку
4) 3 + 0 = 3. Запишем 3
5) Под числом 2 нет слагаемого, поэтому просто сносим его вниз.
Ответ: 23.34

Как вычитать столбиком

Для того, чтобы вычесть два числа столбиком, необходимо записать большее число над меньшим и выполнить последовательное вычитание, например, вычтем столбиком 456 и 89.

456 — 89 = 367

..0
_—456
89

367

1) Из 6-ти вычесть число 9 не получится, так как 6 меньше девяти, поэтому займем 1 у числа 5 и поставим над ним точку, получим вместо числа 6 число 16. Отнимем от 16 число 9; 16 – 9 = 7; запишем 7.

2) Так как мы заняли число 1 у числа 5, то теперь осталось число 4. Из числа 4 вычесть число 8 не получится, поэтому займем 1 у соседнего числа 4 и поставим над ним точку, получим вместо числа 4 число 14. Отнимем от числа 14 число 8 = 6. Запишем 6.

3) Под числом 4 нет вычитаемого, поэтому отнимем от числа 4 число 1 (так как мы занимали 1-цу): 4 -1 = 3; запишем число 3.
Получилось 367.

Приведем еще один пример: 307 – 58

307 — 58 = 249

..0
_—307
58

249

1) Из числа 7 вычесть число 8 не получится, так как 7 меньше 8, поэтому займем 1 у ноля. Поставим над нолем точку. Когда мы занимаем 1-цу у нуля, ноль становится числом 9! получим вместо 0 число 9. Однако у ноля не получится взять единицу, поэтому двигаемся влево и занимаем единицу у числа 3 и ставим над ним точку; отнимем от 17 число 8; 17 – 8 = 9; запишем 9.

2) Так как мы заняли число 1 у ноля, то теперь осталось число 9. Отнимем от числа 9 число 5 = 4. Запишем 4.

3) Под числом 3 нет вычитаемого, но мы помним, что мы заняли единицу у числа 3, поэтому 3-1 = 2. Запишем число 2.
Получилось 249.

Как вычитать столбиком десятичные дроби

Для того, чтобы отнять из десятичной дроби целое число, либо из целого числа вычесть десятичную дробь нужно у целого числа после точки записать столько нолей, сколько чисел после точки у десятичной дроби, затем записать большее число над меньшим.

Например вычтем столбиком из десятичной дроби 123.478 целое число 56

123.478 — 56 = 67.478

..00000
_—123.478
56.000

67.478

Начинаем последовательно вычитать справа налево
1) 8 – 0 = 8. Запишем 8.
2) 7 – 0 = 7. Запишем 7.
3) 4 – 0 = 4. Запишем 4.

4) Ставим точку.
5) Из числа 3 не вычесть число 6, поэтому занимаем единицу у числа 2 и ставим над ним точку. 13 – 6 = 7. Запишем число 7.
6) Над числом 2 стоит точка, значит теперь там уже не число 2, а число 1. Из единицы число 5 не вычесть, поэтому занимаем единицу у числа 1 и ставим над ним точку. 11 – 5 = 6. Запишем число 6.
7) Над числом 1 стоит точка, следовательно, 1 – 1 = 0, поэтому на этом решение законченно.
Ответ: 67.478

Еще один пример на вычитание столбиком десятичной дроби из целого числа.

432 — 2.95

432 — 2.95 = 429.05

0..0.0
_—432.00
2.95

429.05

1) Из ноля число 5 не вычесть, поэтому займем единицу у ноля и поставим над ним точку, далее, как мы уже знаем ставим точку над числом 2 и занимаем единицу. 10 – 5 = 5. Запишем число 5.
2) Над числом 0 стоим точка, следовательно, 0 превратился в число 9. 9 – 9 = 0. Запишем 0.
3) Над числом два стоит точка значит 2-1 = 1. Из числа 1 число 2 не отнять, поэтому занимаем единицу у числа 3 и ставим над ним точку. 11 – 2 = 9. Запишем число 9.
4) Над числом 3 стоит точка, 3 – 1 = 2. Так как нет вычитаемого, просто сносим число 2 вниз, тоже делаем и с числом 4.
Ответ: 429.05

Правила вычитания десятичной дроби из десятичной дроби, такие же как при сложении. Нам так же необходимо сначала совместить точки десятичных дробей и затем выполнить последовательное вычитание справа налево. Вот несколько примеров на вычитание десятичных дробей:

378.326 — 26.57 = 351.756

00.0.00
_—378.326
26.570

351.756

0.07 — 0.009 = 0.061

000.0
_—0.070
0.009

0.061

Как умножать столбиком

Для того, чтобы умножить одно число на другое необходимо записать первый множитель над вторым, причем не важно какой множитель больше первый или второй, но удобнее чтобы записать более компактное решение записать большее число над меньшим. Затем необходимо каждое число нижнего множителя умножить на каждое число верхнего справа налево, затем суммировать произведения.

На примере будет намного понятнее. Итак, умножим 367 на 12

367 × 12 = 4404

_×367
12
734
3670
4404

1. Умножим число 2 на 367 и результат запишем с справа налево от числа 2.

1) 2 × 7 = 14. Запишем число 4, число 1 в уме.
2) 2 × 6 = 12; 12 + 1 = 13. Запишем 3, число 1 в уме.
3) 2 × 3 = 6; 6 + 1 = 7. Запишем число 7. На этом этапе мы получили число 734.

2. Умножим число 1 на 367 и результат запишем справа на лево начиная уже от числа 1 под первой строкой.

1) 1 × 7 = 7. Запишем число 7.
2) 1 × 6 = 6. Запишем число 6.
3) 1 × 3 = 3. Запишем число 3. На этом этапе мы получили число 367

3. Теперь нам необходимо сложить получившиеся два числа 734 и 367

1) Под числом 4 нет слагаемого, поэтом просто снесем его вниз. Запишем число 4.
2) 3 + 7 = 10. Запишем 0 и запомним число 1.
3) 7 + 6 + 1 = 14. Запишем число 4, число 1 в уме.
4) У числа три нет слагаемого, поэтому просто запишет число 3.
На этом решение закончено, получилось 4404.

Как умножать столбиком десятичные дроби

Десятичные дроби столбиком умножать очень просто. Прежде всего, уберем точки из десятичных дробей. Затем произведем умножение уже получившихся целых чисел, далее посчитаем количество чисел в первом и во втором множителе, сложим эти значения, результатом будет число равное количеству чисел после точки в получившемся произведении. На примерах все станет намного понятнее.

Умножим 0.2354 на 12.3997

Уберем точки из десятичных дробей, чтобы было удобной умножать.

_×123997
2354
495988
6199850
37199100
247994000
291888938

Теперь добавим точку в получившейся ответ. Так как в первом множителе 12.3997 после точки стоит 4 числа, и во втором множителе 0.2354 стоит 4 числа, тогда 4 + 4 = 8. Сдедовательно в ответе после точки будет 8 чисел.
2.91888938

_×12.3997
0.2354
2.91888938

Умножим 49.265 на 0.0045

Уберем точки из десятичных дробей, чтобы было удобной умножать.

_×49265
45
246325
1970600
2216925

Теперь добавим точку в получившейся ответ. Так как в первом множителе 49.265 после точки стоит 3 числа, а во втором множителе 0.0045 стоит 4 числа, тогда 3 + 4 = 7. Сдедовательно в ответе после точки будет 7 чисел.
0.2216925

_×49.265
0.0045
0.2216925

Как делить столбиком

Как делить столбиком целые числа.

Деление столбиком с остатком, в данном материале рассматриваться не будет, если интересно, есть много информации по остатку от деления тут.

Разберем для начала как разделить большее число на меньшее в столбик (когда делимое больше делителя).

На примере будет намного нагляднее изучить данную тему. Итак, разделим 12 на 5

12 : 5 = 2.4

01205
01002.4
0020
0020
0000

При делении числа 12 на число 5 у нас получится конечная десятичная дробь. Кому интересно почитать что такое десятичные дроби — это можно сделать здесь.

1) Сколько раз число 5 помещается в числе 12? Правильно 2 раза. Поэтому первым делом умножим 2 на 5 получим 10.
2) Теперь отнимем из числа 12 число 10; 12 – 10 = 2. Запишем число 2.
3) В числе 12 нет больше чисел, поэтому поле числа 2 в ответе необходимо поставить точку. Целую часть ответа мы уже нашли! Двигаемся дальше.
4) Теперь будем находить дробную часть нашей десятичной дроби. Поставим ноль рядом с разностью. Получим число 20. Теперь снова думаем, сколько раз число 5 содержится в числе 20? Правильно 4 раза. 5 × 4 = 20.
5) Отнимем от числа 20 число 20; 20 – 20 = 0. Разность равна нулю, следовательно, результатом деления является конечная десятичная дробь.
Ответ: 2.4

Возьмем другой пример, где уже ответом будет являться бесконечная периодическая десятичная дробь. Разделим 7 на 3

7 : 3 = 2.(3)

0703
0602.3
010
009
001

1) В числе 7 число 3 содержится 2 раза. То есть неполное частное деления числа 7 на число 3 равно числу 2. Умножим число 2 на делитель. 2 × 3 = 6.
2) Отнимем от числа 7 число 6; 7 — 6 = 1; В делимом больше нет чисел, поэтому ставим точку.
3) Начинаем вычислять ответ для дробной части. Для этого к получившейся разности добавим ноль, получим число 10. Неполное частное деления числа 10 на число 3 равно числу 3. Запишем число 3 после точки.
4) 3 × 3 = 9. Из числа 10 отнимем число 9; 10 – 9 = 1. На этом этапе необходимо завершить деление, так как мы уже получали число 1 при вычитании числа 6 из числа 7, следовательно, при дальнейшем решении примера мы снова и снова будем получать число три в виде неполного частного и этот процесс будет продолжаться бесконечно (2. 333333333333333333333333333…). Такое повторение называется периодом бесконечной периодической десятичной дроби. Для краткости период записывают в скобках 2.(3)

Деление десятичных дробей в столбик примеры

Разделим 3.12 на 3.6

Если числитель и знаменатель дроби умножить на одно и тоже число, то значение дроби не изменится, поэтому, чтобы было проще разделить одно число на другое, уберем запятую, домножив оба числа на 100

07120360
036001.97
03520
03240
002800
002520
000280

Разделим 9.4 на 45.1

0940451
00000. 2084257206
0940
0902
003800
003608
0001920
0001804
00001160
00000902
000002580
000002255
0000003250
0000003157
00000000930
00000000902
0000000002800
0000000002706
0000000000094

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N₂ | Двоичная система счисления

N₃ | Троичная система счисления

N₄ | Четырехичная система счисления

N₅ | Пятеричная система счисления

N₆ | Шестеричная система счисления

N₇ | Семеричная система счисления

N₈ | Восьмеричная система счисления

N₉ | Девятеричная система счисления

N₁₁ | Одиннадцатиричная система счисления

N₁₂ | Двенадцатеричная система счисления

N₁₃ | Тринадцатеричная система счисления

N₁₄ | Четырнадцатеричная система счисления

N₁₅ | Пятнадцатеричная система счисления

N₁₆ | Шестнадцатеричная система счисления

N₁₇ | Семнадцатеричная система счисления

N₁₈ | Восемнадцатеричная система счисления

N₁₉ | Девятнадцатеричная система счисления

N₂₀ | Двадцатеричная система счисления

N₂₁ | Двадцатиодноричная система счисления

N₂₂ | Двадцатидвухричная система счисления

N₂₃ | Двадцатитрехричная система счисления

N₂₄ | Двадцатичетырехричная система счисления

N₂₅ | Двадцатипятеричная система счисления

N₂₆ | Двадцатишестеричная система счисления

N₂₇ | Двадцатисемеричная система счисления

N₂₈ | Двадцативосьмеричная система счисления

N₂₉ | Двадцатидевятиричная система счисления

N₃₀ | Тридцатиричная система счисления

N₃₁ | Тридцатиодноричная система счисления

N₃₂ | Тридцатидвухричная система счисления

N₃₃ | Тридцатитрехричная система счисления

N₃₄ | Тридцатичетырехричная система счисления

N₃₅ | Тридцатипятиричная система счисления

N₃₆ | Тридцатишестиричная система счисления

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор со скобками

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка.

Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона.

Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора.

Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

правило, примеры. Калькулятор умножения столбиком

Инструкция

Сначала проверьте навыки ребенка в умножении. Если ребенок нетвердо знает таблицу умножения, то с делением у него тоже могут быть проблемы. Тогда при объяснении деления можно разрешить подглядывать в шпаргалку, но таблицу все-таки придется выучить.

Запишите делимое и делитель через разделительную вертикальную черту. Под делителем вы будете записывать ответ — частное, отделив его горизонтальной чертой. Возьмите первую цифру числа 372 и спросите у ребенка, сколько раз число шесть «помещается» в тройке. Правильно, нисколько.

Тогда возьмите уже две цифры — 37. Для наглядности можно выделить их уголком. Снова повторите вопрос – сколько раз число шесть содержится в 37. Чтобы сосчитать быстро, пригодится . Подберите ответ вместе: 6*4 = 24 – совсем непохоже; 6*5 = 30 – близко к 37. Но 37-30 = 7 – шесть «поместится» еще раз. Наконец, 6*6 = 36, 37-36 = 1 – подходит. Первая цифра частного найдена – это 6. Напишите ее под делителем.

Запишите 36 под цифрой 37, подведите чертой. Для наглядности в записи можно использовать знак . Под чертой поставьте остаток – 1. Теперь «спустите» следующую цифру числа, двойку, к единице – получилось 12. Объясните ребенку, что цифры всегда «спускаются» по одной. Опять спросите, сколько «шестерок» содержит 12. Ответ – 2, на этот раз без остатка. Напишите вторую цифру частного рядом с первой. Окончательный результат – 62.

Также подробно рассмотрите случай деления . Например, 167/6 = 27, остаток 5. Скорее всего, ваш отпрыск про простые дроби пока ничего не слышал. Но если он будет задавать вопросы, что делать с остатком дальше, можно объяснить на примере яблок. 167 яблок разделили между шестью людьми. Каждому досталось 27 штук, и пять яблок остались неподеленными. Можно поделить и их, разрезав каждое на шесть долек и раздав поровну. Каждому человеку досталась одна долька от каждого яблока – 1/6. А так как яблок было пять штук, то и долек у каждого оказалось по пять – 5/6. То есть результат можно записать так: 27 5/6.

Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.

Деление столбиком — удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем — многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.

Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:

Пусть нам нужно разделить 6105 на 55 , запишем:

Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так:

Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.

Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:

Практические навыки удобнее всего отрабатывать на простых примерах. Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8 ÷ 2 = 4 .

Итак, сначала запишем делимое и делитель согласно методу деления в столбик.

Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на 0 , 1 , 2 , 3 . . Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.

Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.

Вернемся к примеру.

2 · 0 = 0 ; 2 · 1 = 2 ; 2 · 2 = 4 ; 2 · 3 = 6 ; 2 · 4 = 8

Итак, мы сразу получили число, равное делимому. Записываем его под делимым, а число 4 , на которое мы умножали делитель, записываем на место частного.

Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае 8 — 8 = 0 .

Данный пример — деление чисел без остатка. Число, получащееся после вычитания — это остаток деления. Если оно равно нулю, значит числа разделились без остатка.

Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число 7 на натуральное число 3 .

В данном случае, последовательно умножая тройку на 0 , 1 , 2 , 3 . . получаем в результате:

3 · 0 = 0 7

Под делимым записываем число, полученное на предпоследнем шаге. По делителем записываем число 2 — неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6 .

В завершение операции вычитаем 6 из 7 и получаем:

Данный пример — деление чисел с остатком. Неполное частное равно 2 , а остаток равен 1 .

Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.

Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа 140288 на число 4 . Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком.

1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14 , так как первая цифра делимого 1 меньше, чем делитель 4 .

2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x = 14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ , включая нуль: 0 , 1 , 2 , 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x . Когда в результате умножения получается число 14 , записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем. Если в результате умножения получается число, большее чем x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.

В соответствии с алгоритмом имеем:

4 · 0 = 0 14 .

Под выделенным числом записываем число 12 , полученное на предпоследнем шаге. На место частного записываем множитель 3 .

3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.

4. Число 2 меньше числа 4 , поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следующую цифру делимого — 0 . В итоге отмечаем новое рабочее число — 20 .

Важно!

Пункты 2 — 4 повторяются циклически до окончания операции деления натуральных чисел столбиком.

2. Снова посчитаем, сколько делителей содержится в числе 20 . Умножая 4 на 0 , 1 , 2 , 3 . . получаем:

Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение.

3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20 — 20 = 0 .

4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2 .

Принимаем это число за рабочее и снова выполняем пункты алгоритма.

2. Умножаем делитель на 0 , 1 , 2 , 3 . . и сравниваем результат с отмеченным числом.

4 · 0 = 0 2

Соответственно, под отмеченным числом записываем число 0 , и под делителем в следующий разряд частного также записываем 0 .

3. Выполняем операцию вычитания и под чертой записываем результат.

4. Справа под чертой добавляем цифру 8 , так как это следующая цифра делимого числа.

Таким образом, получаем новое работчее число — 28 . Снова повторяем пункты алгоритма.

Проделав все по правилам, получаем результат:

Переносим под черту вниз последнюю цифру делимого — 8 . В последний раз повторяем пункты алгоритма 2 — 4 и получаем:

В самой нижней строчке записываем число 0 . Это число записывается только на последнем этапе деления, когда операция завершена.

Таким образом, результатом деления числа 140228 на 4 является число 35072 . Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.

Приведем другие примеры деления чисел в столбик и примеры записи решений.

Пример 1. Деление натуральных чисел в столбик

Разделим натуральное число 7136 на натуральное число 9 .

После второго, третьего и четвертого шага алгоритма запись примет вид:

Повторим цикл:

Последний проход, и поучаем результат:

Ответ: Неполное неполное частное чисел 7136 и 9 равно 792 , а остаток равен 8 .

При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.

Пример 2. Деление натуральных чисел в столбик

Разделим число 7042035 на 7 .

Ответ: 1006005

Деление многозначных натуральных чисел столбиком

Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2 — 4 остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе.Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.

Перемножать большие числа, записывая их в строку, рано или поздно становится довольно сложным и утомительным процессом. Гораздо проще воспользоваться специальным алгоритмом по умножению в столбик: вам не придется держать числа в своей голове и что-либо запоминать. Вы можете делать пометки над столбиком, чтобы всегда видеть, как числа вам нужно перенести. Если вы пытаетесь обучить такому способу ребенка, то очень важно, чтобы таблица умножения отскакивала у него от зубов, иначе, процесс затянется надолго, а сам малыш совершит много ошибок, которые вереницей потянутся по всему примеру. Внимательно прочитайте статью и возьмите такой алгоритм себе на вооружение.

Запишите пример в строчку и посмотрите: какой из множителей меньше? Меньший окажется ниже в записи умножения в столбик, а большой множитель будет стоять наверху.

Запишите пример по такому принципу, как указано на картинке ниже.

Сверху напишите большее число.
Слева поставьте знак умножения в виде крестика.
Снизу запишите меньшее число.
Проведите прямую черту под примером.

Если в примере есть множитель, который оканчивается на ноль или несколько нолей, то его следует записывать так:

Ноли нужно выносить за пример.
Числа пишите под числами.

В таком случае, вы просто переносите это количество нолей сразу в ответ. Если ноли имеются и у первого множителя, и у второго, то сложите их количество и запишите в ответ.

Теперь начинайте расчёт по такому принципу:

Всё верхнее число вы умножаете на последнюю цифру нижнего. Помните, что на последние ноли умножение не производится.
Чтобы вам было удобнее, записывайте числа, которые нужно перенести, сверху над всем примером. Позднее вы можете их просто стереть, зато в процессе вам не придется запоминать числа переноса.
Как только вы закончите расчет, запишите полученное число под чертой.

Как только вы перемножите верхнее число на последнюю цифру нижнего и запишите свой ответ, начинайте перемножать следующее.

По такому же принципу умножьте всё верхнее число на вторую с конца цифру нижнего. Также записывайте числа переноса, однако, ответ вам следует записать под первым решением, но сдвинув запись на одну клеточку левее. У вас получится столбик с выступающей влево строкой.

Как вы уже догадались, вам нужно перемножить верхнее число на все цифры нижнего, начиная с конца. Каждый раз запись ответа переносится на одну клетку левее.

Перемножьте таким образом все числа между собой. Теперь снова проведите черту под столбиком. Между всеми решениями поставьте знак сложения.

Теперь вам осталось выполнить сложение в столбик, которое вы уже должны уметь делать:

Складывайте все числа, находящиеся на одной вертикальной линии.
Если число получается двухзначным, то число десятков вы переносите в следующую вертикальную полосу.

Под некоторыми числами вовсе не будет других – в таком случае, вы просто записываете это число в ответ. Не забывайте переносить в ответ все нули, которые стоят в конце множителей.

Выполнять умножение в столбик очень удобно и быстро, особенно, если требуется перемножить большие числа. Вы легко можете проверить правильность умножения, просто разделив ответ на один из множителей. Для этого используйте калькулятор, либо способ деления уголком. На первых порах такое умножение занимает значительную долю времени, но с опытом, всё действие происходит всего за пару секунд.

Азы деления столбиком и в уме дети изучают в начальной школе: в 3-м или 4-м классе. Но вникают в материал быстро и легко далеко не все третьеклассники. Дома нужно много практиковаться, решать тренировочные примеры. Но сначала лучше еще раз объяснить деление уголком, с остатком, выявить пробелы в детских знаниях.

Как стать суперучителем без специальной подготовки и помочь ребенку с этой трудной темой, расскажем подробнее.

Как научиться делить столбиком

Деление столбиком с остатком и без него нельзя начинать без подготовки. Сначала ребенок должен хорошо уметь и знать следующее:

Отработайте все обозначенные умения до автоматизма. Затем приступайте к делению маленьких цифр на примере таблицы умножения в уме. Например, ребенок выучил, как умножать цифру 6:

Смело предлагайте такие примеры:

Через пару уроков школьник будет выполнять такие задания легко. Можно разнообразить занятия по устному счету играми на деление.

На заметку! Все начальные математические навыки хорошо автоматизируются с помощью онлайн-тестов, где ребенок получает мгновенный результат своей работы.

Игровые задания

Интересные математические игры на деление помогают детям закрепить навык, узнать законы работы с цифрами, освоить устный счет.

Головоломки на развитие внимания. Напишите в тетради 3–5 примеров на деление с ответами. Все, кроме одного, должны быть решены неверно. Нужно быстро найти тот пример, который содержит правильный ответ. Затем исправить остальные с помощью устного счета.
Подбор примера по результату. Предлагайте малышу ответ без примера. Давайте задание придумать задачу. Например, ответ 8. Ребенок может придумать такую задачу: 48:6.
«Идем в магазин». Расставьте на полу игрушки с карточками. На листах написаны примеры: 6:2, 18:3, 42:7, 100:50. Игрушки — это «товар» в фантазийном магазине, частное после решения примера — их цена. Чтобы узнать стоимость покупки, нужно решить задания, а потом оплатить полученный результат в кассу. Играть лучше в небольшой команде — 2–3 человека.
«Молчуны». Ребенок получает карточки с цифрами от 1 до 100. Задавайте вопросы с примерами на деление, ученик должен отвечать без слов, показывая правильный ответ.
Небольшие самостоятельные работы с подарком за старательность. Распечатайте карточки с примерами в количестве 5–10 штук. Укажите время на решение, например 5 минут. Поставьте перед ребенком песочные часы. После выполнения контрольной верно поощрите школьника походом в зоопарк, кино, покупкой книги, сладостей.
«Ищем дерево». Нарисуйте небольшой сад с деревьями на картоне. Каждому растению дайте номер, пусть их будет 10. На листочке для ученика напишите 3 примера:

45:9 120:60 14:7

Школьник должен вычислять результат к каждому заданию, а потом складывать все числа между собой. Получится так:

Ребенок должен найти дерево под номером 9.

Для игры можно использовать цветные пуговицы и ставить их на занятые деревья. Развлечение подходит для командных соревнований.

После устной работы с делением натуральных чисел можно показать ребенку порядок записи примеров столбиком. Если педагогического опыта у вас нет, посмотрите видеоурок на эту тему, вспомните теорию сами.

Теперь можно приступать к объяснению сложного материала школьнику. Есть несколько методик домашнего обучения делению:

1. Мама-учитель

Родителям придется ненадолго стать педагогами. Оборудовать доску, купить мел или маркеры. Заранее вспомнить школьный материал. Объяснить пошагово теорию и закрепить ее на практике с помощью большого количества самостоятельных, карточек, контрольных работ.

2. Посмотреть вместе с ребенком обучающее видео

Например, это:

Затем нужно обсуждать с малышом материал, закреплять навык на практике несколько недель.

3. Нанять репетитора

Деление не самая сложная тема в школьной программе. В начальных классах можно легко обойтись без платных уроков с педагогом. Этот вариант оставим на крайний случай.

На заметку! Обязательно противопоставляйте деление умножению. Проверяйте результат обоих действий противоположным.

Как объяснить деление столбиком

Сначала стоит доходчиво объяснить, что такое деление на простом примере. Суть математического действия — разложить число поровну. В 3-м классе дети хорошо учатся на доступных примерах: раздают кусочки торта гостям, рассаживают кукол по 2 машинам.

Когда малыш усвоит суть деления, покажите его запись на листке. Используйте уже знакомые задания с простыми числами:

Сначала запишите задачу обычным способом: 250:2=?
Каждому числу дайте название: 250 — делимое, 2 — делитель, результат после знака равно — частное.
Затем сделайте сокращенную запись столбиком (уголком):

Рассуждайте вместе так: сначала найдем неполное частное. Это будет 2, так как оно не меньше делителя, а вернее, равно ему. В этом числе помещается один делитель, значит, в частное записываем цифру 1 и умножаем ее на 2. Заносим полученный результат под делимым. Отнимаем 2-2. Получится ноль, поэтому сносим следующее число и опять подыскиваем частное. Совершаем математическое действие до тех пор, пока не получится ноль.
После получения окончательного результат сделайте проверку с помощью умножения: 125х2=250.

Желательно научить третьеклассника рассуждать в процессе вычисления вслух, выполнять действия на черновике. Сначала проговаривайте алгоритм вместе, потом только слушайте ученика и помогайте исправить ошибки.

На заметку! Приучайте малыша постоянно проверять себя. Школьник должен понимать, что величина остатка вычитания в столбике деления должен всегда быть меньше делителя.

Деление на однозначное число

Возьмите листок и ручку, посадите ребенка рядом. Сначала запишите пример уголком сами. Для деления на однозначное число выбирайте такие цифры, которые дают результат без остатка (полный ответ).

Первый урок можно построить так:

Положите перед ребенком картинку с образцом деления столбиком.
Придумайте собственный пример. Пусть это будет 254:2
Задание нужно записывать уголком. Доверьте это школьнику. Он может посмотреть, как делается запись на картинке.
Спросите третьеклассника: «Какое число нужно делить на 2 первым?». В этот момент важно объяснять, что делимое должно быть равно или большего делителя. Малыш выделит для деления первое число из данной цифры: 2… 54
Теперь определите вместе, сколько двоек поместится в числе 2. Ответ: 1.
Записываем частное под уголком.
Умножаем 1 на 2 и записываем результат под делимым.
Вычитаем.
Так как получился 0, сносим следующую цифру под линию после вычитания: 5.
Опять задаем вопрос: «Сколько двоек поместится в 5?» Малыш вспоминает таблицу умножения или подбирает частное с помощью логики. Отвечает: 2.
Записываем 2 в частное, умножаем на 2.
Результат (4) записываем под 5.
Отнимаем.
Остается 1. Единицу разделить на 2 нельзя, поэтому сносим остатки делимого вниз. Получается 14.
Делим 14 на 2. Записываем в частное 7.
Умножаем на 2. Записываем под чертой 14.
Отнимаем.
В конце всегда должен получаться 0.
В результате у ребенка сформируется такая запись:

Для закрепления запишите еще 3–5 примеров на деление на этом же листочке. Не отходите далеко от школьника, образец не прячьте, не превращайте урок в проверочную работу. Малыш только учится делить. На этом этапе помогайте ему, подсказывайте и наталкивайте на правильное решение для повышения уверенности в себе.

На заметку! Для автоматизации навыка деления столбиком можно составить небольшую памятку, где прописан каждый этап математического действия. Разрешайте школьнику смотреть в нее до тех пор, пока он сам не забудет об образце.

Деление на двузначное число

Когда ученик 3-го класса усвоил деление на однозначное число, можно приступать к следующему этапу — работе с двузначными цифрами. Начинайте с простых, явных примеров, чтобы малыш понял алгоритм действий. Например, возьмите числа 196 и 28 и объясните принцип:

Сначала подберите примерное число для ответа. Для этого выясните приблизительно, сколько цифр 28 поместится в 196. Для удобства можно округлять оба числа: 200:30. Получится не больше 6. Полученное число не нужно записывать, это только догадка.
Проверяем результат умножением: 28х6. Получается 196. Предположения оказались верными.
Запишите ответ: 196:28 =6.

Еще один вариант обучения: деление на двузначное число уголком. Такой способ больше подходит для работы с числами от четырех разрядов, то есть тысяч. Приведем простой пример:

Напишите на листе бумаги 4070, начертите уголок и подпишите делитель — 74.
Определите, с какого числа начнете делить. Спросите у ребенка, можно ли разделить 4 на 74, 40? В результате малыш поймет, что сначала нужно ограничиться числом 407. Очертите полученную цифру сверху полукругом. 0 останется в стороне.
Теперь нужно выяснить, сколько 74 поместится в 407. Действуем с помощью логики и проверки умножением. Получится 5. Записываем результат под уголком (под делителем).
Теперь умножаем 74 на 5 и записываем результат под делимым. Получится 370. Важно начинать запись с первого числа слева.
После записи нужно подвести горизонтальную черту и отнять 370 от 407. Получится 37.
37 разделить на 74 нельзя, поэтому вниз сносится оставшийся в верхнем ряду 0.
Теперь делим 370 на 74. Подбираем множитель (5) и записываем его под уголком.
Умножаем 5 на 74, записываем результат в столбик. Получится 370.
Опять получаем разность. Результат будет равен 0. Значит, деление считается завершенным без остатка. 4070:74=55. Частное смотрим под уголком.

Для проверки правильности решение произведите умножение: 74х55=4070.

Есть мнение! Иметь в доме решебник с ГДЗ многие родители считают недопустимым. А зря. С помощью готовых заданий ребенок может легко проверить себя. Главное — правильно объяснить школьнику назначение сборника ДЗ с ответами.

Многозначные числа

Сложнее всего детям даются задачи на трехзначные и четырехзначные числа. Четверокласснику тяжело оперировать тысячами и сотнями тысяч. У школьника возникают следующие проблемы:

Не может определить неполное число делимого для первого действия. Вернитесь к изучению разрядов натуральных чисел, поработайте над развитием внимания малыша.
Пропускает 0 в записи частного. Это самая распространенная проблема. В результате у ребенка получается число на несколько разрядов меньше правильного. Чтобы избежать этой ошибки, нужно распечатывать памятку с последовательностью действий в примерах, где в середине частного есть нули. Предложите ребенку тренажер с такими заданиями для отработки навыка.

При обучении решению задач с крупными числами действуйте поэтапно:

Объясните, что такое неполное делимое и зачем его выделять.
Потренируйтесь в поиске делимого устно без последующего решения задач. Например, дайте детям такие задания:

Найдите неполное частное в примерах: 369:28; 897:12; 698:36.

Теперь приступайте к решению на бумаге. Запишите столбиком: 1068:89.
Сначала нужно отделить неполное делимое. Можно использовать запятую сверху над числами.

На заметку! Примеры с семизначными цифрами с третьеклассниками решать не нужно. Это лишнее. Достаточно остановиться на заданиях с пятизначными числами (до 10 000). Деление миллионов дети проходят в старших классах.

Деление с остатком

Завершающим этапом уроков на закрепление навыка деления будет решение заданий с остатком. Они обязательно встретятся в решебнике для 3–4-го класса. В гимназиях с математическим уклоном школьники изучают не только неполные числа, но и десятичные дроби. Форма записи примера уголком останется прежней, отличаться будет только ответ.

Примеры на деление с остатком берите несложные, можно преобразовывать уже решенные задания с целым числом в ответе, прибавляя к делимому единицу. Это очень удобно для ребенка, он сразу увидит, чем примеры похожи и чем отличаются.

Урок может выглядеть так:

На заметку! Отделять целое число от остатка запятой, делать из него дробное на начальном этапе обучения делению не нужно. Записывайте остаток отдельно, чтобы школьник видел конечный результат разности в столбике.

Как делать проверку

Проверка деления производится с помощью умножения: делитель умножается на делитель. Делать это можно столбиком:

Теперь проверим:

Для проверки деления с остатком нужно:

Умножить полное частное на делитель.
Прибавить к результату остаток.

34+1 (остаток) =35

Алгоритм проверки правильности решения примера деления не изменяется от разрядности цифр.

Важно! Первое время просите ребенка расписывать проверку умножением подробно, чтобы проверить и закрепить знание таблицы.

Примеры для тренировки

Научиться быстро решать примеры с делением помогают тренировочные задания. Карточками может оканчиваться каждый урок после прохождения новой темы.

Однозначные

Двузначные

Многозначные

Скачать карточки

В качестве домашнего математического тренажера используйте карточки с примерами. В них включайте разные случаи: с однозначными и многозначными числами, деление с полным результатом и остатком. Скачать карточки можно бесплатно. Раздаточный материал обязательно следует напечатать для проверочной работы.

Ошибки с делением у детей в начальной школе встречаются довольно часто. Уделите этой теме максимум внимания и времени, чтобы усвоение последующего материала проходило без запинок. Используйте карточки, видеоуроки, постоянную тренировку навыка и повторение пройденных тем в игровой форме. Тогда домашние уроки не навеют на ребенку скуку и пройдут с максимальной пользой.

ВАЖНО ! *при копировании материалов статьи обязательно указывайте активную ссылку на перво

Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.

Деление – интересная операция, в чем мы и убедимся с вами в этой статье!

Деление чисел

Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.

Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.

Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».

Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.

Деление с остатком

Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.

Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).

Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).

Деление на 3 и 9

Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:

Найти сумму цифр делимого.

Поделить на 3 или 9 (в зависимости от того, что вам нужно).

Если ответ получается без остатка, то и число поделится без остатка.

Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.

Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.

Умножение и деление

Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.

Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.

Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.

Деление 3 класс

В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:

Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?

Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?

Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?

Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?

Деление 4 класс

Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:

Деление в столбик

Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.

Рассмотрим пример, 512:8.

1 шаг . Запишем делимое и делитель следующим образом:

Частное будет записано в итоге под делителем, а расчеты под делимым.

2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:

3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:

Теперь 51 больше 8. Это неполное частное.

4 шаг . Ставим точку под делителем.

5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:

6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:

7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:

8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.

* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:

10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.

Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.

Деление трехзначных

Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.

Деление дробей

Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):

Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.

Деление числа на классы

Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.

Деление натуральных чисел

Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Деление презентация

Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!

Примеры на деление

Легкий уровень

Средний уровень

Сложный уровень

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Визуальная геометрия»

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Копилка»

Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение перезагрузка»

Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.

Высокоточный калькулятор

Комментарий / запрос: , пожалуйста, сделайте это проще, но оставьте место для большого количества цифр

Цель использования: Расчет факториалов большого числа
Комментарий / запрос: Было бы здорово, если бы цифр было больше, хотя

Комментарий / запрос: было бы здорово, если бы было больше цифр

Цель использования: №
Комментарий / запрос: × не работает
из Кейсана: Используйте звездочку (*) для умножения.(-1)
Калькулятор сломан, я не вижу чисел или прокручиваю влево. Вы должны создать кнопку, чтобы скрыть список функций, чтобы он выглядел так, как раньше, а также, возможно, кнопку вкладки вверху, чтобы отобразить цифровую клавиатуру. Рассмотрим степень, выраженную в виде 17 26 чисел 37 0-квадратов. Также мне нравятся шаблоны клавиатуры для чисел, которые симметрично противоположны, например 857142 + 142857, они добавляют к BASE — 1 в каждом месте цифры.

Цель использования: Числа Фиббо / Люка в биномиальном расст.утилиты
Комментарий / запрос: интегрировать кнопки константы фина и / или последовательности Фибоначчи

Цель использования: Проверить, может ли тело дрейфовать в пространстве (дрейфовать, как при повороте с автомобилем и скольжении колеса по дороге).

Цель использования: Проверка гипотезы о кратных простых числах
Комментарий / запрос: Простой интерфейс и примеры позволили легко научиться пользоваться.
Несколько выражений и ответов помогают отслеживать тестирование.
Мне нужна была только 22-значная точность — пока — но даже это редкость в мире вычислительных систем с 15 значащими цифрами.
Спасибо!

Цель использования: расчетный объем шара толщиной 1 метр

Цель использования: альтернативно физическому расчету

Определение алгоритма Merriam-Webster

al · go · ритм | \ ˈAl-gə-ˌri-t͟həm \ : процедура решения математической задачи (как найти наибольший общий делитель) за конечное число шагов, которая часто включает повторение операции. широко : пошаговая процедура решения проблемы или достижения какой-либо цели. Существует несколько поисковых систем, крупнейшими игроками которых являются Google, Yahoo и Bing.Каждая поисковая система имеет собственное запатентованное вычисление (называемое «алгоритмом»), которое ранжирует веб-сайты по каждому ключевому слову или комбинации ключевых слов. — Джули Бринтон… иногда вы решаете проблему, придумывая какой-то алгоритм. Но иногда вы решаете проблему очень специальным образом. — Уильям Х. Хаггинс

применений обучения с подкреплением в реальном мире | автор: garychl

II.Приложения

Эта часть написана для обычных читателей. В то же время он будет более ценным для читателей, знакомых с RL.

Управление ресурсами в компьютерных кластерах

Разработка алгоритмов распределения ограниченных ресурсов для различных задач является сложной задачей и требует эвристики, созданной человеком. В документе «Управление ресурсами с глубоким обучением с подкреплением» [2] показано, как использовать RL для автоматического обучения распределению и планированию ресурсов компьютера для ожидающих заданий с целью минимизировать среднее замедление выполнения заданий.

Пространство состояний было сформулировано как текущее распределение ресурсов и профиль ресурсов заданий. Что касается области действия, они использовали уловку, позволяющую агенту выбирать более одного действия на каждом временном шаге. Вознаграждение представляло собой сумму (-1 / продолжительность работы) по всем заданиям в системе. Затем они объединили алгоритм REINFORCE и базовое значение, чтобы вычислить градиенты политики и найти лучшие параметры политики, которые дают распределение вероятностей действий для минимизации цели.Щелкните здесь, чтобы просмотреть код на Github.

Управление светофором

В статье «Многоагентная система на основе обучения с подкреплением для управления сигналами сетевого трафика» [3] исследователи попытались разработать контроллер светофора для решения проблемы перегрузки. Однако, протестированные только в смоделированной среде, их методы показали лучшие результаты, чем традиционные методы, и пролили свет на потенциальное использование многоагентного RL при проектировании системы трафика.

Транспортная сеть с пятью перекрестками.Источник.

Пять агентов были помещены в транспортную сеть с пятью перекрестками, с агентом RL на центральном перекрестке для управления сигнализацией трафика. Состояние было определено как восьмимерный вектор, каждый элемент которого представляет относительный транспортный поток на каждой полосе движения. Агенту было доступно восемь вариантов, каждый из которых представлял комбинацию фаз, а функция вознаграждения была определена как уменьшение задержки по сравнению с предыдущим временным шагом. Авторы использовали DQN, чтобы узнать значение Q пар {состояние, действие}.

Робототехника

Существует огромная работа по применению RL в робототехнике. Читателям предлагается обратиться к [10] для обзора RL в робототехнике. В частности, [11] обучил робота изучать правила сопоставления необработанных видеоизображений с действиями робота. Изображения RGB подавались на CNN, а выходными данными были крутящий момент двигателя. Компонент RL представлял собой управляемый поиск политик для генерации обучающих данных, полученных из его собственного распределения состояний.

Демо статьи.

Конфигурация веб-системы

В веб-системе имеется более 100 настраиваемых параметров, и процесс настройки параметров требует наличия опытного оператора и многочисленных проверок на наличие ошибок.В статье «Подход с подкреплением к автоконфигурации онлайн-веб-системы» [5] показана первая попытка автономной реконфигурации параметров в многоуровневых веб-системах в динамических средах на основе виртуальных машин.

Процесс реконфигурации можно сформулировать как конечный MDP. Пространство состояний представляло собой конфигурацию системы, пространство действий — {увеличение, уменьшение, сохранение} для каждого параметра, а вознаграждение определялось как разница между заданным целевым временем отклика и измеренным временем отклика.Авторы использовали безмодельный алгоритм Q-обучения для выполнения задачи.

Хотя авторы использовали некоторые другие методы, такие как инициализация политики, чтобы исправить большое пространство состояний и вычислительную сложность проблемы вместо потенциальных комбинаций RL и нейронной сети, считается, что новаторская работа проложила путь для будущих исследований в эта зона.

Химия

RL также может применяться для оптимизации химических реакций. [4] показали, что их модель превосходит современные алгоритмы, и обобщены на разные базовые механизмы в статье «Оптимизация химических реакций с помощью глубокого обучения с подкреплением».

В сочетании с LSTM для моделирования функции политики агент RL оптимизировал химическую реакцию с помощью марковского процесса принятия решений (MDP), характеризуемого {S, A, P, R}, где S — набор экспериментальных условий (например, температура, pH и т. д.), A — это набор всех возможных действий, которые могут изменить условия эксперимента, P — вероятность перехода от текущего условия эксперимента к следующему условию, а R — вознаграждение, которое является функцией состояния.

Приложение отлично подходит для демонстрации того, как RL может сократить трудоемкую работу, выполняемую методом проб и ошибок, в относительно стабильной среде.

Персонализированные рекомендации

Предыдущая работа над новостными рекомендациями столкнулась с рядом проблем, включая быстро меняющуюся динамику новостей, пользователям быстро надоедает, а рейтинг кликов не может отражать уровень удержания пользователей. Guanjie et al. применили RL в системе рекомендаций новостей в документе под названием «DRN: Структура глубокого обучения с подкреплением для рекомендаций новостей» для борьбы с проблемами [1].

На практике они создали четыре категории функций, а именно: A) функции пользователя и B) функции контекста как характеристики состояния среды и C) функции новостей пользователя и D) функции новостей как функции действий.Четыре характеристики были введены в Deep Q-Network (DQN) для расчета Q-значения. Список новостей был выбран для рекомендации на основе Q-значения, и нажатие пользователя на новости было частью вознаграждения, полученного агентом RL.

Авторы также использовали другие методы для решения других сложных проблем, включая воспроизведение памяти, модели выживания, Dueling Bandit Gradient Descent и так далее. Пожалуйста, обратитесь к бумаге для получения подробной информации.

Торги и реклама

Исследователи из Alibaba Group опубликовали статью «Назначение ставок в реальном времени с многоагентным подкрепляющим обучением в медийной рекламе» [6] и заявили, что их распределенное кластерное решение для мультиагентных торгов (DCMAB) достигло многообещающие результаты, и поэтому они планируют провести живое тестирование на платформе Taobao.

Подробности реализации оставлены на усмотрение пользователей. Вообще говоря, рекламная платформа Taobao — это место, где продавцы могут делать ставки, чтобы показывать рекламу покупателям. Это может быть проблема с несколькими агентами, потому что продавцы делают ставки друг против друга, и их действия взаимосвязаны. В документе продавцы и клиенты были сгруппированы в разные группы, чтобы снизить вычислительную сложность. Пространство состояний агентов показало статус затрат-доходов агентов, пространство действий было предложением (непрерывным), а вознаграждение было доходом, вызванным кластером клиентов.

Алгоритм DCMAB. Источник: https://arxiv.org/pdf/1802.09756.pdf

В статье также изучались другие вопросы, в том числе влияние различных настроек вознаграждения (корыстные или согласованные) на доходы агентов.

Игры

RL так хорошо известен в наши дни, потому что это основной алгоритм, используемый для решения различных игр и иногда для достижения сверхчеловеческой производительности.

RL против линейной модели против человека. Щелкните здесь, чтобы найти источник.

Самыми известными должны быть AlphaGo [12] и AlphaGo Zero [13].AlphaGo, обученная бесчисленным человеческим играм, уже достигла сверхчеловеческих качеств, используя сеть ценностей и поиск по дереву Монте-Карло (MCTS) в своей сети политик. Тем не менее, позже исследователи подумали и попробовали более чистый подход RL — обучить его с нуля. Исследователи позволили новому агенту AlphaGo Zero поиграть с самим собой и наконец победить AlphaGo 100-0.

Глубокое обучение

В последнее время можно увидеть все больше и больше попыток объединить RL и другую архитектуру глубокого обучения, и они показали впечатляющие результаты.

Одной из самых влиятельных работ в RL является новаторская работа Deepmind по объединению CNN с RL [7]. Поступая таким образом, агент получает возможность «видеть» окружающую среду через сенсорную систему больших измерений, а затем учиться взаимодействовать с ней.

RL и RNN — еще одна комбинация, которую люди использовали для опробования новой идеи. RNN — это тип нейронной сети, у которой есть «воспоминания». В сочетании с RL, RNN дает агентам возможность запоминать вещи. Например, [8] объединил LSTM с RL для создания Deep Recurrent Q-Network (DRQN) для игры в игры Atari 2600.[4] также использовали RNN и RL для решения задачи оптимизации химических реакций.

Deepmind показал [9], как использовать генеративные модели и RL для создания программ. В модели агент, обученный противником, использовал сигнал в качестве вознаграждения для улучшения действий, вместо того, чтобы распространять градиенты во входное пространство, как при обучении GAN.

Входные данные против сгенерированного результата. См. Источник.

Онлайн-математические заметки Паулса

Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки

Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. , вероятно, вы пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Добро пожаловать в мои онлайн-уроки и заметки по математике.Цель этого сайта — предоставить полный набор бесплатных онлайн (и загружаемых) заметок и / или руководств для классов, которые я преподаю в Университете Ламара. Я попытался написать заметки / учебные пособия таким образом, чтобы они были доступны для всех, кто хочет изучить предмет, независимо от того, посещаете ли вы мои классы или нет. Другими словами, они не предполагают, что у вас есть какие-либо предварительные знания, кроме стандартного набора обязательных материалов, необходимых для этого класса. Другими словами, предполагается, что вы знаете алгебру и триггер до чтения заметок по исчислению I, знаете исчисление I до чтения заметок по исчислению II, и т. Д. .Предположения о вашем прошлом, которые я сделал, даются с каждым описанием ниже.

Я хотел бы поблагодарить Шейна Ф., Фреда Дж., Майка К. и Дэвида А. за все опечатки, которые они нашли и прислали мне! Я пытался проверить эти страницы и отловить как можно больше опечаток, однако невозможно отловить их все, если вы также являетесь тем, кто написал материал. Фред, Майк и Дэвид поймали довольно много опечаток, которые я пропустил, и были достаточно любезны, чтобы отправить их мне.Еще раз спасибо, Фред, Майк и Дэвид!

Если вы один из моих нынешних студентов и ищете здесь домашние задания, у меня есть набор ссылок, которые приведут вас на нужные страницы, перечисленные здесь.

В настоящее время я получил онлайн-заметки / учебные пособия по моей алгебре (Math 1314), Calculus I (Math 2413), Calculus II (Math 2414), Calculus III (Math 3435) и дифференциальным уравнениям (Math 3301). У меня также есть пара обзоров / дополнений. Среди обзоров / дополнений, которые у меня есть, есть обзор алгебры / триггера для моих студентов, изучающих математику, учебник по комплексным числам, набор общих математических ошибок и несколько советов по изучению математики.

Я также сделал большинство страниц этого сайта доступными для загрузки. Эти загружаемые версии представлены в формате pdf. Каждая тема на этом сайте доступна для полной загрузки, и в случае очень больших документов я также разделил их на более мелкие части, которые в основном соответствуют каждой из отдельных тем. Чтобы получить загружаемую версию любой темы, перейдите к этой теме, а затем в меню Загрузить вам будет предложена возможность загрузить тему.

Вот полный список всех тем, которые в настоящее время доступны на этом сайте, а также краткие описания каждой из них.

Шпаргалки по алгебре — это как можно больше общих фактов, свойств, формул и функций алгебры, которые я мог придумать. Также есть страница с распространенными алгебраическими ошибками. Доступны две версии шпаргалки. Один полноразмерный и в настоящее время состоит из четырех страниц. Другая версия — это уменьшенная версия, которая содержит точно такую же информацию, что и полная версия, за исключением того, что она только что была уменьшена, поэтому две страницы печатаются на лицевой стороне и две страницы печатаются на обратной стороне одного листа бумаги.

Шпаргалки по триггерам — это набор общих фактов, свойств и формул триггеров. Также включен единичный круг (полностью закрашенный). Доступны две версии шпаргалки. Один полноразмерный и в настоящее время состоит из четырех страниц. Другая версия — это уменьшенная версия, которая содержит точно такую же информацию, что и полная версия, за исключением того, что она только что была уменьшена, поэтому две страницы печатаются на лицевой стороне и две страницы печатаются на обратной стороне одного листа бумаги.

Шпаргалки по исчислению — это серия шпаргалок по исчислению, охватывающая большую часть стандартного курса «Исчисление I» и несколько тем из курса «Исчисление II».Здесь есть четыре разных шпаргалки. Один содержит всю информацию, другой — только информацию о ограничениях, один — только информацию о производных, а последний — только информацию об интегралах. Каждая шпаргалка представлена в двух версиях. Один полноразмерный, а другой уменьшенный, с точно такой же информацией, что и полноразмерная версия, печатающая две страницы на лицевой и / или оборотной сторонах каждой страницы.

Общие производные и интегралы — это набор общих производных и интегралов, которые несколько регулярно используются в классе «Исчисление I» или «Исчисление II».Также включены напоминаний о нескольких методах интеграции. вот доступны две версии шпаргалки. Один полноразмерный и в настоящее время состоит из четырех страниц. Другая версия — это уменьшенная версия, которая содержит точно такую же информацию, что и полная версия, за исключением того, что она только что была уменьшена, поэтому две страницы печатаются на лицевой стороне и две страницы печатаются на обратной стороне одного листа бумаги.

Таблица преобразований Лапласа — вот список преобразований Лапласа для класса дифференциальных уравнений.В этой таблице приведены многие из часто используемых преобразований и формул Лапласа. В настоящее время это две страницы, первая страница — это преобразования Лапласа, а вторая — некоторая информация / факты о некоторых записях.

Все классы, за исключением дифференциальных уравнений, имеют практические задачи (с решениями), которые вы можете использовать на практике, а также набор задач с заданиями (без решений / ответов), которые преподаватели могут использовать, если они того пожелают.

Алгебра (математика 1314) [Примечания] [Практические задачи] [Проблемы с назначением] — В этот набор примечаний / учебного пособия включены следующие темы:

Предварительные сведения — свойства экспоненты, рациональные показатели, отрицательные показатели, радикалы, многочлены, факторинг, рациональные выражения, комплексные числа
Решение уравнений и неравенств — линейные уравнения, квадратные уравнения, завершение квадрата, квадратичная формула, приложения линейных и квадратных уравнений, приводимые к квадратичной форме, уравнения с радикалами, линейные неравенства, полиномиальные и рациональные неравенства, уравнения абсолютных значений и неравенства.
Графики и функции — Графические линии, окружности и кусочные функции, определение функций, обозначение функций, композиция функций, обратные функции.
Общие графы — параболы, эллипсы, гиперболы, абсолютное значение, квадратный корень, постоянная функция, рациональные функции, сдвиги, отражения, симметрия.
Полиномиальные функции — деление многочленов, нули / корни многочленов, поиск нулей многочленов, отображение многочленов, частичные дроби.
Экспоненциальные и логарифмические функции — экспоненциальные функции, логарифмические функции, решение экспоненциальных функций, решение логарифмических функций, приложения.
Системы уравнений — метод подстановки, метод исключения, расширенная матрица, нелинейные системы.

Примечания / учебник по алгебре предполагают, что вы имели некоторое представление об основах алгебры. В частности, предполагается, что разделы показателей и факторинга будут для вас в большей степени обзором.Также предполагается, что вы ознакомились с основами построения графиков уравнений. Построение графиков конкретных типов уравнений подробно рассматривается в примечаниях, однако предполагается, что вы понимаете основную систему координат и способы построения точек.

Calculus I (Math 2413) [Примечания] [Практические задачи] [Проблемы с назначением] — В этот набор примечаний / учебного пособия включены следующие темы:

Обзор алгебры / триггера — триггерные функции и уравнения, экспоненциальные функции и уравнения, логарифмические функции и уравнения.
Пределы — понятия, определение, вычисления, односторонние ограничения, непрерывность, ограничения, связанные с бесконечностью, Правило L’Hospitals
Производные — определение, интерпретации, формулы производных, правило степени, правило произведения, правило факторного, цепное правило, производные высшего порядка, неявное дифференцирование, логарифмическое дифференцирование, производные триггерных функций, экспоненциальные функции, логарифмические функции, обратные триггерные функции и гиперболические функции Функции.
Применение производных финансовых инструментов — связанные ставки, критические точки, минимальные и максимальные значения, функции увеличения / уменьшения, точки перегиба, вогнутость, оптимизация
Интегрирование — определение, неопределенные интегралы, определенные интегралы, правило замены, вычисление определенных интегралов, основная теорема исчисления
Приложения интегралов — среднее значение функции, площадь между кривыми, тела вращения, работа.

Примечания / учебник по исчислению I предполагают, что у вас есть практические знания алгебры и триггера. Есть некоторый обзор нескольких тем по алгебре и триггерам, но по большей части предполагается, что у вас есть приличный опыт в алгебре и триггерах. Эти заметки не предполагают никаких предварительных знаний о математическом анализе.

Calculus II (Math 2414) [Примечания] [Практические проблемы] [Проблемы с назначением] — В этот набор примечаний / учебного пособия включены следующие темы:

Методы интеграции — интеграция по частям, интегралы с участием триггера Функции, подстановки триггеров, интегрирование с использованием дробных дробей, интегралы С участием корней, интегралов с участием квадратичных структур, стратегии интеграции, несобственные Интегралы, сравнительный тест для несобственных интегралов и аппроксимация определенных Интегралы.
Применение интегралов — длина дуги, площадь поверхности, центр масс / центроид, гидростатическое давление и сила, вероятность.
Параметрические уравнения и полярные координаты — параметрические уравнения и кривые, расчет с параметрическими уравнениями (касательные, площади, длина дуги и площадь поверхности), полярные координаты, расчет с полярными координатами (касательные, площади, длина дуги и площадь поверхности).
Последовательности и серии — Последовательности, серии, сходимость / расхождение серий, абсолютная серия, интегральный тест, сравнительный тест, предельный сравнительный тест, чередующийся последовательный тест, коэффициент соотношения, корневой тест, оценка значения серии, степенная серия, серия Тейлора , Биномиальный ряд
Векторы — основы, величина, единичный вектор, арифметика, точечное произведение, крест Изделие, Проекция
Трехмерная система координат — уравнения линий, уравнения плоскостей, квадратичные поверхности, функции нескольких переменных, векторные функции, пределы, производные и интегралы векторных функций, касательные векторы, векторы нормалей, бинормальные векторы, кривизна, цилиндрические координаты, сферические Координаты

Заметки / учебник по исчислению II предполагают, что у вас есть рабочие знания по исчислению I, включая ограничения, производные и интеграцию (вплоть до базовой замены).Также предполагается, что вы достаточно хорошо знакомы с Trig. Некоторые темы сильно зависят от триггеров и знания триггерных функций.

Calculus III (Math 3435) [Примечания] [Практические задачи] [Проблемы с назначением] — В этот набор примечаний / учебного пособия включены следующие темы:

Трехмерная система координат — уравнения линий, уравнения плоскостей, квадратичные поверхности, функции нескольких переменных, векторные функции, пределы, производные и интегралы векторных функций, касательные векторы, нормальные векторы, бинормальные векторы, кривизна, цилиндрические координаты, Сферические координаты
Частные производные — лимиты, частные производные, частичные производные высшего порядка Производные, дифференциалы, цепное правило, производные по направлениям, градиент.
Приложения частных производных — касательная плоскость, нормальная линия, относительные экстремумы, абсолютные экстремумы, оптимизация, множители Лагранжа.
Кратные интегралы — повторяющиеся интегралы, двойные интегралы, двойные интегралы в полярных координатах, тройные интегралы, тройные интегралы в цилиндрических координатах, тройные интегралы в сферических координатах, изменение переменных, площадь поверхности.
линейные интегралы — векторные поля, линейные интегралы относительно длины дуги, линейные интегралы относительно x и y , линейные интегралы векторных полей, фундаментальная теорема линейных интегралов, консервативные векторные поля, потенциальные функции, теорема Грина, Curl, Дивергенция.
Поверхностные интегралы — параметрические поверхности, поверхностные интегралы, поверхностные интегралы векторных полей, теорема Стокса, теорема о расходимости.

Примечания / руководство по Calculus III предполагают, что у вас есть рабочие знания Calculus I, включая ограничения, производные и интеграцию. Также предполагается, что читатель хорошо знаком с несколькими темами Calculus II, включая некоторые методы интегрирования, параметрические уравнения, векторы и знание трехмерного пространства.

Дифференциальные уравнения (Math 3301) [Примечания] — В этот набор примечаний / учебного пособия включены следующие темы:

Дифференциальные уравнения первого порядка — линейные уравнения, разделимые уравнения, точные уравнения, равновесные решения, проблемы моделирования.
Дифференциальные уравнения второго порядка — однородные и неоднородные дифференциальные уравнения второго порядка, основной набор решений, неопределенные коэффициенты, изменение параметров, механические колебания
Преобразования Лапласа — определение, обратные преобразования, ступенчатые функции, функции Хевисайда, дельта-функция Дирака, решение IVP, неоднородная IVP, IVP с непостоянным коэффициентом, интеграл свертки.
Системы дифференциальных уравнений — форма матрицы, собственные значения / собственные векторы, фазовая плоскость, неоднородные системы, преобразования Лапласа.
— серийные решения, дифференциальные уравнения Эйлера.
Дифференциальные уравнения высшего порядка — n ^th дифференциальные уравнения порядка, неопределенные коэффициенты, изменение параметров, системы дифференциальных уравнений 3 x 3.
Краевые задачи и ряды Фурье — Краевые задачи, собственные значения и собственные функции, ортогональные функции, ряды синуса Фурье, ряды косинусов Фурье, ряды Фурье.
Уравнения в частных производных — уравнение тепла, волновое уравнение, уравнение Лапласа, разделение переменных.

Эти примечания не предполагают предварительного знания дифференциальных уравнений. Однако требуется хорошее владение математическим анализом. Это включает практические знания дифференциации и интеграции.

Algebra / Trig Review — это обзор алгебры и Trig Review это было первоначально написано для моих студентов исчисления I. Это все еще в основном студентам, изучающим математику, с редкими комментариями о том, как будет использоваться в классе Calculus.Однако любой, кому нужен обзор некоторых основной алгебры, триггеры, экспоненциальные функции и логарифмы должны найти информация об использовании.

Не все темы, затронутые в классе алгебры или триггера, охвачены в этом рассмотрение. В основном я затрагивал темы, которые имеют особое значение для студентов. в классе исчисления. Я включил пару тем, которые не так важны в класс по математике, но у студентов, кажется, иногда возникают проблемы с этим. Если позволит время, я буду добавлять и другие разделы.

Обзор представляет собой набор задач с первым решением, содержащий подробную информацию о том, как работать с этим типом проблемы. Более поздние решения обычно не так подробны, но могут содержать дополнительную / новую информацию по мере необходимости.

Учебник по комплексным числам — это краткое введение в некоторые из основных идей, связанных с комплексными числами. Обсуждаемые темы — это краткий обзор арифметики с комплексными числами, комплексного сопряжения, модуля, полярной и экспоненциальной формы, а также вычислительных мощностей и корней комплексных чисел.

Обратите внимание, что этот учебник предполагает, что вы хотя бы видели некоторые комплексные числа перед чтением. Цель этого документа — выйти за рамки того, что большинство людей видит, когда впервые знакомится с комплексными числами, скажем, на уроках алгебры в колледже. Кроме того, этот документ никоим образом не предназначен для того, чтобы дать полное представление о комплексных числах, и я не охватываю все задействованные концепции (это целый класс сам по себе).

Распространенные математические ошибки — как и в случае с алгеброй / триггером, просмотрите это изначально был написан для моего класса по исчислению I.Однако только один из пяти Разделы, которые я привел здесь, напрямую относятся к теме исчисления. В другие четыре раздела относятся к более общим ошибкам или охватывают ошибки алгебры и триггера. В первых четырех разделах есть пара примеров исчисления, но в Во всех этих случаях я также пытался привести примеры, не связанные с исчислением.

Эта часть сайта должна быть интересна всем, кто ищет общие математические ошибки. Если вы не изучаете математику или не изучали математику, вы следует просто игнорировать последний раздел.

Как изучать математику — это небольшой раздел с некоторыми советами о том, как лучше всего изучать математику.

Большая лекция: подробности и примеры

В рамках проекта преобразования больших лекций профессор Андерсленд преобразовал свой необходимый инженерный класс «Электрические схемы» при поддержке Джейн Рассел, сотрудника Центра обучения OTLT. В то время как раньше классное время тратилось на доставку контента, а практика решения проблем происходила вне класса, преобразованный курс включает инновационное использование технологии, которая позволяет студентам взаимодействовать с материалом в классе при поддержке профессора.Теперь ученики готовятся перед занятием к теме дня, просматривая короткие онлайн-лекции и учебные пособия и работая над вводными практическими задачами. В начале урока профессор Андерсленд читает короткую мини-лекцию, чтобы отточить понимание учащимися. В оставшейся части урока учащиеся применяют концепции дня, решая оцениваемые задачи, поставленные с помощью онлайн-платформы для домашних заданий. Платформа обеспечивает немедленную обратную связь, и учащимся предоставляется три возможности правильно решить задачу, чтобы заработать баллы.Понимая, что начинающие инженеры часто допускают предсказуемые ошибки или наталкиваются на одни и те же дисциплинарные узкие места, профессор Андерсленд запрограммировал подсказки для каждого упражнения на онлайн-платформе, чтобы помочь студентам точно решать и понимать проблемы.

Поскольку каждый учащийся сталкивается с проблемами, которые связаны с одной и той же концепцией с немного разными числами, учащиеся работают друг с другом, чтобы изучить процесс, а не просто поделиться ответами. Курс профессора Андерсленда гарантирует, что студенты достигают пика своего потенциального уровня развития, работая над проблемами в классе, под руководством инструктора, помощников учителя и сверстников.

Работая с Управлением преподавания, обучения и технологий, профессор Андерсленд участвует в программе «Стипендия преподавания и обучения» (SOTL), систематически изучая и размышляя об изменениях, которые он внес в свой курс, и делится результатами с другими. Результаты первых исследований показывают, что студенты лучше подготовлены, более вовлечены, получают более высокие баллы по оценкам и сообщают о более позитивном восприятии полезности курса.

Почему критическое мышление важно в бизнесе?

Критическое мышление можно определить как процесс анализа и оценки информации для определения убеждений или действий.Например, когда учащиеся выбирают, куда поступить в колледж, они используют критическое мышление, взвешивая преимущества и недостатки различных школ, в которые они были приняты, с учетом соответствующей информации, такой как стоимость и местоположение. Критическое мышление влечет за собой не только получение информации, но и ее анализ для выявления основных элементов.

Почему критическое мышление важно в бизнесе? Бизнес-лидеры ежедневно предпринимают важные действия: от приема на работу и увольнения до проверки отчетов о финансовых доходах, участия в заседаниях совета директоров и урегулирования кризисов в сфере связей с общественностью.Это именно те области, в которых критическое мышление вступает в игру, поскольку бизнес-лидеры используют этот навык для принятия сложных решений, таких как увольнение сотрудника или выпуск пресс-релиза, когда скандал угрожает запятнать репутацию компании. Профессионалы, стремящиеся развить свои навыки критического мышления, могут извлечь выгоду из получения степени магистра искусств в области делового общения онлайн.

Роль критического мышления в бизнесе

Применяя критическое мышление в бизнесе, лидер должен использовать логику для выявления, понимания, анализа и решения проблем.Это требует терпения и практики. Успешное применение критического мышления часто приводит к более эффективным рабочим процессам.
Следующие три примера помогают понять, почему критическое мышление важно в бизнесе:

Улучшение коммуникационных стратегий. Общение с разными типами людей требует определения потребностей целевой аудитории, что требует критического мышления. Например, если компания покупается конкурентом, генеральный директор должен подумать, как это повлияет на всех, от низкоуровневых сотрудников до инвесторов, и определить, какие сообщения передать каждой стороне.Очень важно действовать быстро, так как он или она должен первым сообщить сотрудникам новости, чтобы сохранить их доверие.

Поддержка бесперебойной работы. Поддержание повседневной деятельности в постоянно меняющейся среде требует постоянного критического мышления. Например, если в ресторане отключено электричество и нет аварийного генератора, менеджер должен решить не только, что делать с клиентами и персоналом, но и нужно ли и как утилизировать охлажденные продукты. Чем быстрее действует менеджер, тем больше у него шансов извлечь максимальную пользу из неудачной ситуации.

Оптимизация разработки продуктов. Роль по разработке продукта требует принятия множества решений для обеспечения эффективности, конкурентоспособности и безопасности. Например, если компания продает новый кухонный гаджет, его разработка определенным образом сделает его более привлекательным, но такой дизайн также может затруднить его использование. Следует ли компании уделять приоритетное внимание функциям или моде? Чем раньше будет принято решение, тем скорее можно будет начать производство.

В каждом из этих примеров критическое мышление напрямую влияет на эффективность на рабочем месте.

Спрос на критическое мышление в бизнесе

Критическое мышление считается мягким навыком. В отличие от сложных навыков, таких как знание иностранного языка, навыки межличностного общения, характеризуемые как «мягкие», трудно поддаются количественной оценке. Коммуникация, лидерство и командная работа — примеры мягких навыков; их нельзя «измерить» с помощью теста или чисел, но они узнаваемы по тому, как люди взаимодействуют с другими. Хотя профессиональные навыки, о которых свидетельствуют оценки, сертификаты или демонстрируемые компетенции (например, скорость набора текста), являются частью того, на что обращают внимание рекрутеры, они — только часть общей картины.

Рынок труда все больше признает важность навыков межличностного общения. Фактически, согласно совместному отчету PayScale и Future Workplace за 2016 год, около 60% менеджеров по найму считают, что недавним выпускникам не хватает навыков решения проблем и критического мышления.

Учитывая, что критическое мышление важно в бизнесе, профессионалы должны приложить усилия, чтобы развить этот мягкий навык. Критическое мышление, как и решение проблем, может быть приобретенным навыком, если приложить немало усилий, чтобы практиковать и овладевать им.

Моделирование или настройки реального мира могут предоставить профессионалам основу для развития этого навыка. Более того, чтобы иметь влияние на бизнес, критическое мышление должно дополняться четким и уверенным общением (еще один мягкий навык). Даже профессионалы, разбирающиеся в бизнесе, скорее всего, не добьются успеха, если не смогут поделиться своими мыслями с руководителями, менеджерами или коллегами.

Как критическое мышление и коммуникация связаны в бизнесе

Если коммуникация относится к содержательному обмену информацией в организации, критическое мышление — это двигатель, который обеспечивает смысл.Умение идентифицировать проблему и разработать убедительное объяснение и решение важно для делового общения.

Онлайн-программа магистра делового общения

Rider University обучает этим навыкам и предоставляет студентам возможность отточить свои таланты. Это позволяет людям учиться на 100% онлайн и получить степень менее чем за два года.

Студенты могут научиться применять критическое мышление и коммуникативные навыки для успеха в бизнесе следующими способами:

Оценка различных ситуаций в деловой среде. Возьмем, к примеру, главу маркетинговой группы, управляющей девятью людьми. Чтобы разработать маркетинговое предложение для нового продукта, он делит свою команду на три группы по три человека. Каждая группа предлагает свою концепцию. Затем руководитель маркетинговой группы выбирает одного, обосновывая свой выбор четкой коммуникацией, которая вознаграждает тех, чья концепция была выбрана, не расстраивая других. Это одна из многих ситуаций, которые могут возникнуть в деловой среде, требующей критического мышления при общении.

Взаимодействие между командами / отделами. Лидерам необходимо управлять внутренними коммуникациями своих команд, а также их взаимодействием с другими командами. Например, вышеупомянутой группе маркетинга, возможно, придется работать напрямую с группой разработки продукта, чтобы определить наиболее заметные преимущества продукта. В этом случае курс, ориентированный на коммуникацию и организационную культуру, подготавливает менеджеров к осознанию того, что отдел разработки продуктов может иметь совершенно другой повседневный подход к работе и сотрудничеству.

Работа в команде. Лидерам необходимо уметь ориентироваться в различиях между группами людей с разным происхождением. Онлайн-курс «Магистр делового общения» Райдера включает в себя курсовые работы, которые фокусируются на многокультурных аспектах совместной работы в организации и могут быть полезным инструментом в бизнесе.

Презентационные стратегии. Критическое мышление позволяет людям принимать решения, влияющие на бизнес, и с уверенностью делиться своими выводами.Например, физическое лицо должно представить результаты финансового квартала, а цифры показывают убыток. Он может признать, что это связано с крупными инвестициями в новый инструмент повышения производительности труда, который, по прогнозам, увеличит оборот и приведет к большой прибыли в следующем квартале. Курсовая работа программы бизнес-презентации дает профессионалам возможность сделать такое суждение.

Устное общение. Лидерам, возможно, придется использовать словесные навыки, чтобы изменить мнение другого человека в бизнесе.Например, если они сидят в правлении, и правление голосует по важному вопросу, результатом которого является равенство голосов, они могут пожелать высказаться и представить аргумент в пользу своей стороны. Курсовая работа, посвященная методам убедительного дискурса, дает студентам навыки, необходимые для изменения мнения и поведения людей.

Письменное сообщение. Не все бизнес-кейсы проводятся в личных беседах. Например, лидеры могут вдохновлять свои команды с помощью мощного электронного письма.Курс стратегического делового письма предоставляет студентам инструменты, необходимые для использования их навыков письма для поддержки стратегии и достижения желаемых результатов, таких как мотивация сотрудников.

Узнайте больше о магистра в области делового общения

Теперь, когда у вас есть более четкое представление о том, почему критическое мышление важно в бизнесе, подумайте о том, чтобы отточить этот навык с помощью онлайн-курса магистра делового общения Университета Райдера. Эта онлайн-программа обучает инструментам, которые необходимы вам для управления бизнесом.Как новатор в своей организации, вы сможете превзойти ожидания. Если вы мечтаете стать лидером, эта степень может направить вас на правильный путь. Узнайте больше о программе Райдера сегодня.

Рекомендуемая литература:

Карьера в сфере делового общения и как выбрать подходящего

Как специалисты по коммуникациям в области здравоохранения могут гарантировать соблюдение этических норм в сфере здравоохранения

Пять ценных навыков делового общения для корпоративных лидеров

Источники:

The Balance Careers, «Hard Skills vs.Soft Skills: в чем разница? »

Chicago Tribune , «Навыки критического мышления сейчас пользуются наибольшим спросом в продажах и бизнесе»

Journal of Leadership Education, «Давайте поспорим: использование дебатов для обучения критическому мышлению и коммуникативным навыкам будущих лидеров»

PayScale, «Отчет о готовности рабочей силы и навыков к выпуску 2016 года по PayScale и будущему рабочему месту»

PayScale, «Эти 5 мягких навыков помогут вам нанять»

Основы критического мышления «Определение критического мышления»

4 простых идеи для MVP, которые стоит попробовать

Мы собираемся изучить минимально жизнеспособные примеры продуктов, которые помогут вам точно определить, что продавать в Интернете.

ПРИМЕЧАНИЕ: Эта статья содержит бесплатных обучающих видео , которые вы можете посмотреть прямо на этой странице. Прокрутите вниз, чтобы начать.

Я знаю, что разработка вашего первого онлайн-предложения — большой шаг.

Но у вас надо взять . Почему? Потому что…

Пока вы на самом деле не предложите что-то на продажу, вы не ведете бизнес — вы управляете благотворительной организацией!

Связано: Как построить свой бизнес в Интернете, полное руководство

Минимально жизнеспособный продукт — это то, что стоит между вами и онлайн-доходами.

В этой всеобъемлющей презентации минимально жизнеспособного продукта я собираюсь показать вам:

Почему вам следует разработать минимально жизнеспособный продукт , прежде чем создавать более сложное решение
Чего ожидать от первого минимума жизнеспособный продукт
Минимальный жизнеспособный продукт, примеры и идеи , которые вы можете использовать для начала работы

Может показаться, что сделать это за месяц — непростая задача.

А если использовать здесь минимально жизнеспособные примеры продуктов и идеи? Вы можете запустить свое предложение, получить доход и узнать, что работает в ближайшие 30 дней.

Связано: 3 этапа беспроблемного первого запуска продукта

Получите бесплатный шаблон минимально жизнеспособного продукта PDF

Бесплатно! Укажите свое имя и адрес электронной почты ниже, и я пришлю вам свой бесплатный планировщик минимально жизнеспособных предложений .

If включает заполняемый шаблон, в котором вы можете продумать, что вы включите в свое предложение.

Вы откроете для себя мой «трехмерный подход» для создания быстрого и простого минимально жизнеспособного предложения, которое вы можете использовать для проверки своей следующей идеи.

Plus, получите подробное руководство по минимально жизнеспособным примерам продуктов, приведенным в этой статье.

Что такое минимально жизнеспособный продукт (MVP)?

Для остального мира MVP означает «Самый ценный игрок».

Если вы тренер спортивной команды, это именно тот человек, которого вы вводите в игру, потому что знаете, что он забьет для вашей команды больше.

В этой статье у меня есть другое определение MVP.

MVP означает Minimum Viable Product — или Minimum Viable Service , если у вас бизнес, основанный на предоставлении услуг.

Лично? Я хотел бы думать об этом как о вашем минимальном жизнеспособном онлайн-предложении , , который является глобальным термином, включающим либо продукт, либо услугу.

Это было бы MVOO!

Что напоминает мне…

Ваш MVP — или MVOO — это то, как вы проверяете свои бизнес-идеи в отношении доходов.

MVP станет вашим самым ценным игроком, потому что он избавит вас от множества неприятностей.

Это позволит вам проверить свою большую идею и убедиться, что вы ее правильно поняли, прежде чем вы вложите все свои усилия в создание чего-то очень сложного и трудоемкого, что, как оказалось, никому не нужно.

Вместо этого…

Вы собираетесь разработать что-то небольшое, что даст результат, чтобы вы могли проверить, действительно ли это работает.

На случай, если вам интересно, напротив минимально жизнеспособного продукта выглядит так:

Вы тратите недели, месяцы — а иногда и лет — на создание решения, даже не проверяя, хочет ли его кто-нибудь
Вы изучаете, наблюдаете и сравниваете свое будущее решение с предложениями других людей — и обнаруживаете, что своего не хватает, поэтому возвращаетесь к чертежной доске
Вы откладываете выпуск своего предложения до тех пор, пока не сможете «сделать все правильно», что не может происходит, пока вы его не отпустите!

Это мерзкий замкнутый круг — невозможно вести бизнес.

Давайте избежим этой участи и создадим минимально жизнеспособный продукт или услугу простым способом.

Почему вы должны создавать минимально жизнеспособное онлайн-предложение?

Вам следует создать минимально жизнеспособный продукт, потому что он позволяет вам протестировать целый ряд важных концепций, получая при этом доход.

Вы создадите минимально жизнеспособное предложение, чтобы узнать о таких вещах, как:

Люди хотят ваше решение?
Сможете ли вы продать свое решение?
Будет ли кто-нибудь заплатить за ваше решение?
Предлагает ли ваше решение реальных результатов ?

Сосредоточьтесь на предоставлении реальной ценности в простом и легком для создания пакете.

Самая важная черта, которую следует помнить о минимально жизнеспособном предложении, — это то, что решает проблему , а имеет значение — но в то же время легко и быстро создать.

Какова цель минимально жизнеспособного продукта?

Когда вы занимаетесь большим проектом, например, создаете свое первое онлайн-предложение, важно действительно понимать проблему, которую вы пытаетесь решить.

Какова конечная цель вашего минимально жизнеспособного предложения? Посмотрите видео ниже, чтобы понять эту важную концепцию.

Видео движется слишком медленно для вас? Сделайте это:

Ваша конечная цель — решить проблему, о которой вы, возможно, не подозреваете.

Проблема, которую мы решаем, заключается не в том, «Мне нужен товар».

Проблема, которую мы решаем, — это ваш пробел в знаниях .

Верно! Вначале вам нужно знать так много:

Вам нужно знать , какие проблемы у ваших клиентов проблемы
Вам нужно знать , как вы сможете осуществить какую-то трансформацию для своих клиентов
Вы нужно знать вопросов и недоразумений ваших клиентов их собственными словами
Вам нужно знать , есть ли реальный интерес к вашему решению, прежде чем вы будете его чрезмерно разрабатывать

Это сложная задача, но я ‘ я получил твою спину!

Приведенные ниже минимально жизнеспособные примеры продуктов помогут вам начать работу.

Связано: Как начать бизнес в Интернете и преодолеть его вызов №1

Связано: Пошаговое руководство по созданию названий продуктов, которые понравятся вашим клиентам

Где я могу найти минимально жизнеспособные примеры продуктов?

Давайте посмотрим на реальные примеры минимально жизнеспособных продуктов, услуг или предложений. *

* Все приведенные ниже минимально жизнеспособные примеры продуктов взяты у людей, создающих онлайн-бизнес в моей коучинговой программе BIG League.

Пример минимально жизнеспособного продукта 1: Улучшение отношений

Предположим, у вас есть бизнес, который будет направлен на улучшение отношений.

Вы могли бы разработать минимально жизнеспособное предложение, которое все примерно — здоровый подход к ведению сложных разговоров . Здоровое общение — часть решения для здоровых отношений!

Это может быть короткая серия занятий, проводимых вживую (подробнее о том, как предоставить минимально жизнеспособное предложение, см. Ниже).

Пример минимально жизнеспособного продукта 2: Увеличение дохода в Интернете

Допустим, у вас есть бизнес, который помогает людям получать больше доходов в Интернете.

Вы можете создать минимально жизнеспособный продукт, состоящий из , как создавать страницы продаж с высокой конверсией. Эффективные страницы продаж помогут вам получить больше дохода в Интернете.

Вы решаете небольшую проблему, которая является частью более серьезной задачи, стоящей перед вашим идеальным клиентом по вашей теме.

Пример минимально жизнеспособного продукта 3: Хорошее здоровье

Допустим, у вас есть бизнес, направленный на то, чтобы помочь людям улучшить здоровье людей среднего возраста и старше.

Ваш минимально жизнеспособный продукт — это все примерно , как составить план здорового питания.

Здоровое питание — это часть уравнения: питательная пища улучшает наше общее состояние здоровья.

Пример минимально жизнеспособного продукта 4: Счастливый выход на пенсию

Допустим, у вас есть бизнес, в котором все сводится к тому, как добиться успешного выхода на пенсию.

Вы создаете минимально жизнеспособный продукт, который состоит из , как каждую неделю находить свою цель.

Решайте чьи-то неделя и неделя за неделей, вы помогаете им лучше провести месяц, год и десятилетие.

Минимально жизнеспособный продукт Пример 5: Бизнес, основанный на услугах

С бизнесом, основанным на услугах, немного сложнее, но, допустим, у вас есть бизнес по копирайтингу и написанию контента.

Вы можете создать минимально жизнеспособный продукт, чтобы помочь людям написать свою онлайн-биографию для своей страницы «О нас», своих профилей в социальных сетях или биографии автора сообщения в блоге. Каждому нужна хорошая биография — а написать свою собственную, как известно, сложно.

Помогите им написать эту короткую копию, и они оценят ваши услуги.Вы узнаете их как людей и сможете связаться с теми, кто кажется вам хорошими кандидатами на ваши услуги.

Какие простые идеи минимально жизнеспособного продукта [MVP] я могу попробовать?

Мы рассмотрели примеры MVP и идеи для вашего MVP.

Но по моему опыту работы с членами BIG League, у них нет недостатка в идеях.

Это , воплощающий в жизнь непростых идей.

К счастью, существует множество недорогих инструментов, которые упрощают предоставление минимально жизнеспособного предложения.

В видео ниже я делюсь четырьмя минимально жизнеспособными идеями доставки продукта.

Любой из минимально жизнеспособных примеров продуктов, приведенных в предыдущем разделе, может быть доставлен с использованием любого из форматов, указанных в следующем разделе. Смешивать и сочетать!

Форматы доставки для всех четырех примеров минимально жизнеспособных продуктов имеют некоторые общие черты:

Эти минимально жизнеспособные примеры продуктов дают вам возможность напрямую взаимодействовать с вашими клиентами — вы узнаете их проблемы и то, как они описывают их.
Все минимально жизнеспособные примеры продуктов здесь требуют очень небольшой подготовки. Вы можете наметить, что хотите охватить, и создавать информацию по ходу дела.

Посмотрите это видео, чтобы узнать все подробности:

Идея доставки минимально жизнеспособного продукта 1: Короткий семинар

Короткий семинар — моя любимая идея минимально жизнеспособного продукта на сегодняшний день.

Это живое мероприятие, которое длится от одного до трех, сочетающее обучение и ответы на вопросы.

Вы будете приглашать людей, которые соответствуют вашему идеальному профилю клиента.

Как провести небольшой семинар:

Зарегистрируйтесь для получения учетной записи Zoom для встреч. Это самое простое и дешевое решение. Настройте встречу в Zoom и скопируйте ссылку на встречу. Настройте Zoom для записи встречи.
Приглашайте людей по электронной почте. Когда они покупают мастерскую, вы отправляете им ссылку на встречу.
Отправить напоминания. Перед встречей отправьте напоминания — люди будут заняты и могут забыть.
Загрузить запись собрания. Возьмите свою копию видео встречи на вкладке «Записи» в Zoom.
Загрузите запись семинара на YouTube. Сделайте его скрытым, а затем вставьте записываемое видео на страницу своего веб-сайта, защищенную паролем.

Это очень и очень простой способ передать эту информацию.

Вы продаете полезный семинар и доставляете его вживую, чтобы люди могли участвовать в этом моменте, а также получать пользу от просмотра повтора.

Вот что вы узнаете, составив небольшой семинар:

Вы увидите, действительно ли людям нужно ваше решение.
Вы узнаете, что люди понимают и чего они не понимают, когда вы научите их своей теме.
Вы также почувствуете, о чем еще они беспокоятся.
Вы увидите, что их смущает в вашей теме.

Минимально жизнеспособная поставка продукта Идея 2: Индивидуальное обучение

Индивидуальное обучение очень легко осуществить.

Это может быть от одного до нескольких сеансов коучинга с одним человеком, и это может включать последующее письмо по электронной почте.

Конечно, вы хотите пригласить людей, которые соответствуют вашему идеальному профилю клиента.

Как проводить индивидуальные тренинги:

Зарегистрируйтесь для получения учетной записи собрания Zoom. Используйте переговорную комнату по умолчанию для советов по наставничеству. (Каждая учетная запись собрания Zoom поставляется с комнатой собрания по умолчанию.) Настройте Zoom для записи собрания.
Отправьте ссылку на комнату для встреч по умолчанию человеку, которого вы тренируете. Отправьте его по электронной почте до встречи.
Отправьте напоминание перед сеансом коучинга , чтобы ваш клиент пришел вовремя.
Поделитесь загружаемой записью. Загрузите видеофайл из Zoom и поместите его в Dropbox или Google Drive, где ваш клиент сможет взять его и сохранить.

Вот что вы узнаете из коучинга один на один:

Вы научите людей находить собственные решения — и увидите, какие препятствия стоят на их пути. они разбираются в вещах и открывают новые способы, которыми вы можете их направлять
Вы увидите, какое из ваших учений находит отклик и помогает больше всего — так что вы сможете делать больше этого в будущем

Имейте в виду, что вы не делаете вещи для ваших коучинговых клиентов — это ошибка многих неопытных коучей! Они не наняли вас в качестве подрядчика, чтобы делать что-то для них.Вы поддерживаете их, пока они работают над своими собственными решениями.

Приготовьтесь по-настоящему заглянуть за кулисы того, с чем борются ваши клиенты-коучеры.

Помните, что сидеть напротив идеального покупателя — это настоящая привилегия, поэтому не тратьте его зря. Делайте хорошие заметки и усваивайте все, что можете.

Минимально жизнеспособная идея доставки продукта 3: Групповое обучение

Краткое групповое обучение — это очень простая идея минимально жизнеспособного продукта.

Это прямая трансляция из одного-трех сеансов, которая проводится для небольшой группы людей — максимум шести или восьми человек.

Задайте для группового коучинга тему, чтобы все задаваемые вопросы касались конкретной задачи, которую вы хотите в конечном итоге решить с помощью более крупного продукта.

Опять же, вы хотите пригласить людей, которые соответствуют вашему идеальному профилю клиента.

Как проводить групповое обучение:

Зарегистрируйтесь для получения учетной записи собрания Zoom. Настройте встречу в Zoom и скопируйте ссылку на встречу. Настройте Zoom для записи встречи.
Приглашайте людей по электронной почте. Когда они покупают групповое обучение, вы отправляете им ссылку на собрание Zoom.
Отправить напоминания. Перед сессией отправьте напоминание по электронной почте.
Загрузить запись собрания. Возьмите копию обучающего видео на вкладке «Записи» в Zoom.
Загрузите запись тренировки на YouTube. Сделайте его скрытым, а затем вставьте записываемое видео на страницу своего веб-сайта, защищенную паролем.

Вот что вы узнаете из краткосрочного группового коучинга:

Вы тренируете людей, чтобы они находили собственные решения, и поддерживаете их, когда они разбираются.
Вы воочию увидите их камни преткновения и проблемы
Вы поможете им пройти через процесс трансформации и узнаете, как помочь осуществить эту трансформацию.

Опять же, помните, что сидеть напротив идеального покупателя — это настоящая привилегия, поэтому не теряйте его зря. Слушай внимательно.

Вы готовы помочь им, но вы тоже можете многому у них научиться.

Минимально жизнеспособная поставка продукта Идея 4: Услуга «дегустатор»

Услуга «дегустатор» является идеальным примером минимально жизнеспособного продукта, если у вас есть бизнес, основанный на предоставлении услуг.

Попробуйте пробную версию вашего более крупного предложения услуг, чтобы клиенты могли увидеть, каково с вами работать.

Как предоставить дегустатора услуг:

Создайте небольшую, простую в предоставлении услугу , ориентированную на людей, которые соответствуют вашему идеальному профилю клиента.
Нацельтесь на лицо, принимающее решения. Создайте небольшое предложение для людей, которые в будущем будут заключать с вами крупные контракты на оказание услуг.
Разработайте тестер услуг , который позволит клиентам получить представление о том, каково работать с вами над проектом. Проявите творческий подход!
Будьте проще. Общайтесь с клиентами по электронной почте, посредством видеовстреч или телефонных звонков и делайте это очень личным, чтобы потенциальные клиенты взаимодействовали с вами — поставщиком услуг.

Вот что вы узнаете, предложив дегустатору услуг:

Вы узнаете, будет ли легко работать с потенциальными клиентами в качестве клиентов, и это действительно важная информация, потому что, если вы обнаружите, что их трудно работать, вы не собираетесь предлагать им другие вещи.
Вы также узнаете, в чем состоят потребности ваших потенциальных клиентов, и сможете предложить им услуги, соответствующие этим потребностям.

Примеры минимально жизнеспособных продуктов здесь имеют одну общую черту …

Помните: все примеры минимально жизнеспособных продуктов в этой статье имеют что-то общее.

Вы напрямую взаимодействуете со своим клиентом.

Это одна из причин, по которой я не рекомендую электронную книгу в качестве минимально приемлемого предложения или запись короткой серии видео.

Вы тоже можете это сделать, но все идеи, которые я описал в этой статье, позволяют вам напрямую взаимодействовать с вашим клиентом, и это очень ценно.

Вам не нужно представлять, как они отреагируют на ваше решение — вы убедитесь в этом сами!

Вы можете использовать их вопросы и текущие проблемы, чтобы сделать свое предложение лучше, яснее и эффективнее.

Вы не можете получить это из электронной книги или заранее записанного видео.

Как оценить результаты вашего минимально жизнеспособного предложения

Вы выставили свое минимально жизнеспособное предложение всему миру — поздравляем!

Как вы оцениваете свои минимально жизнеспособные результаты предложения, а затем продвигаетесь вперед?

Практическое правило для онлайн-продуктов заключается в том, что от трех до пяти процентов людей, увидевших предложение, в конечном итоге совершат покупку.Если от трех до пяти процентов людей, увидевших предложение, в конечном итоге купят, у вас все в порядке.

Для сервисов конвертация будет другая. Это будет зависеть от вашего предложения и вашей отрасли. Было бы разумно начать этот процесс с какой-то целью, имея в виду минимальное количество, которое вы хотели бы продать.

Общайтесь со своими клиентами

Помните, как только вы завершите это минимально жизнеспособное предложение, попросите обратную связь и будьте действительно готовы выслушать все, что вам говорят люди.

Ваши клиенты будут разделять хорошее, но они могут разделить плохое, и это также важно знать, потому что вы хотите иметь возможность улучшать свое предложение со временем.

Проверьте себя

Вы также хотите проверить себя. Вам действительно понравилось предлагать это минимально жизнеспособное предложение?

Если вам не понравилось предоставлять свое предложение, может быть, вам нужно изучить другую идею?
Если вам понравилось предлагать минимально жизнеспособное предложение, то пора сделать еще больше.

Говоря о большем, проверьте, не просят ли ваши клиенты больше:

Хотели бы они больше семинаров?
Хотят ли они продолжить работу с небольшой группой, с которой они познакомились в вашей программе?
Они спрашивают, могут ли они забронировать больше сеансов или вы можете предоставить им больше своих услуг?

Любой из этих ответов действительно отличный знак!

Следующие шаги для вашего минимально жизнеспособного продукта

Вот как превратить ваше минимально жизнеспособное предложение в продукт или услугу, приносящие доход:

На основе отзывов клиентов разработайте немного более сложное решение, чем то, которое вы предоставили в первый раз из ворот и доставьте его снова
Получите больше опыта, соберите больше отзывов, сделайте его сильнее и сделайте свое предложение лучше!
Улучшите свое позиционирование: это означает, как вы представляете свое предложение, как вы говорите о нем и как вы его продаете.
Улучшайте свою доставку: найдите способ упростить его использование, отслеживание и получение результатов.

Делайте все возможное, чтобы улучшить минимально жизнеспособное предложение и делать его лучше каждый раз, когда вы его предлагаете.

Начните получать доход с минимально жизнеспособного продукта или услуги

Используйте приведенные здесь минимально жизнеспособные примеры продуктов, чтобы создать онлайн-предложение, которое поможет вам:

Узнайте, в чем заключаются проблемы ваших клиентов — и какие слова они используют для описания их
Узнайте, как вы можете обеспечить реальную трансформацию для своих клиентов
Узнайте, есть ли реальный интерес к вашему решению, прежде чем тратить время и деньги на его разработку

Добавьте этот пост в закладки и возвращайтесь к нему, когда вам нужно создать минимальное выгодное предложение.

Готовы начать сейчас? Возьмите ресурс ниже и сделайте первый шаг.