Построение графика функции онлайн | umath.ru
- Обязательно писать все знаки умножения
- Десятичные дроби нужно разделять точкой
- Список функций и констант смотрите ниже
Как пользоваться программой:
- Можно строить графики сразу нескольких функций. Для этого просто разделяйте функции точкой с запятой (;).
- Масштаб изменяется с помощью кнопок «+» и «−». Кнопка «100%» меняет масштаб на стандартный.
- Положение экрана можно менять, перетаскивая его мышью, а можно стрелками на панели слева.
- Кнопка «·» в центре джойстика переносит начало координат в центр экрана.
- Кнопка «↺» изменяет масштаб на стандартный и переносит начало координат в центр.
- В форме под графиком можно выбрать точку, которую нужно расположить в центре экрана.
Режимы
Обычный. В этом режиме можно строить графики функций, заданных уравнением
Параметрический. Этот режим предназначен для построения графиков кривых, заданных параметрически
Полярные координаты. Режим позволяет построить график кривой, заданной в полярной системе
координат, то
есть уравнением где — радиальная координата, а — полярная координата.
Режим позволяет построить график кривой, заданной в полярной системе
координат, то
есть уравнением где — радиальная координата, а — полярная координата.
Список констант
| Константа | Описание |
|---|---|
pi | Число =3,14159... |
e | Число Эйлера =2,71828... |
Список функций
| Функция | Описание |
|---|---|
+ − * / | Сложение, вычитание, умножение, деление |
( ) | Группирующие скобки |
abs() или | | | Модуль числа. Выражение abs(x) эквивалентно |x|. Если функция содержит модуль под
модулем, то пользуйтесь abs(). Например, если вы хотите построить график функции |1-x+|x+5||,
то нужно вводить abs(1-x+abs(x+5)). 3 дают 3 дают x в третьей
степени |
sqrt() | Квадратный корень |
sin() | Синус |
cos() | Косинус |
tg() | Тангенс |
ctg() | Котангенс |
arcsin() | Арксинус |
arccos() | Арккосинус |
arctg() | Арктангенс |
arcctg() | Арккотангенс |
ln() | Натуральный логарифм числа |
lg() | Десятичный логарифм числа |
log(a, b) | Логарифм числа b по основанию a |
| Степень числа e |
sh() | Гиперболический синус |
ch() | Гиперболический косинус |
th() | Гиперболический тангенс |
cth() | Гиперболический котангенс |
График функции
Графиком функции называется множество точек плоскости таких, что абсциссы и ординаты
этих точек удовлетворяют уравнению .
Программа создана для школьников и студентов и позволяет строить графики функций онлайн. Во многих браузерах (например, Google Chrome) картинку с графиком функции можно сохранить на компьютер.
Пожалуйста, все предложения и замечания по работе программы пишите в комментариях.
Кроме того мы планируем создать библиотеку функций с интересными и забавными графиками. Если вы открыли функцию с таким графиком, то обязательно напишите об этом в комментариях! Ваше открытие будет опубликовано и станет носить ваше имя ;).
Построение графиков — Sage Tutorial in Russian v9.2
Sage может строить двумерные и трехмерные графики.
Двумерные графики
В двумерном пространстве Sage может отрисовывать круги, линии и
многоугольники; графики функций в декартовых координатах; также графики
в полярных координатах, контурные графики и изображения векторных полей.
Некоторые примеры будут показаны ниже. Для более исчерпывающей информации
по построению графиков см.
Данная команда построит желтую окружность радиуса 1 с центром в начале:
sage: circle((0,0), 1, rgbcolor=(1,1,0)) Graphics object consisting of 1 graphics primitive
Также можно построить круг:
sage: circle((0,0), 1, rgbcolor=(1,1,0), fill=True) Graphics object consisting of 1 graphics primitive
Можно создавать окружность и задавать ее какой-либо переменной. Данный пример не будет строить окружность:
sage: c = circle((0,0), 1, rgbcolor=(1,1,0))
Чтобы построить ее, используйте c.show() или show(c):
c.save('filename.png') сохранит график в файл.
Теперь эти „окружности“ больше похожи на эллипсы, так как оси имеют разный масштаб. Это можно исправить следующим образом:
sage: c.show(aspect_ratio=1)
Команда Хороший способ создания заполненных фигур — создание списка точек ( Напечатайте Можно добавить текст на график: Учителя математики часто рисуют следующий график на доске: не одну
ветвь arcsin, а несколько, т. Так как функция тангенса имеет больший интервал, чем синус, при
использовании той же техники для перевертывания тангенса требуется
изменить минимальное и максимальное значения координат для оси x: Sage также может строить графики в полярных координатах, контурные
построения и изображения векторных полей (для специальных видов функций).
Далее следует пример контурного чертежа: Sage также может быть использован для создания трехмерных графиков. Этот калькулятор предназначен для преобразования координат в пространстве, заданных в трех системах: Определяет точку в пространстве при помощи трех чисел : x, y, z. Каждое число соответствует длине кратчайшего отрезка, проложенного параллельно одноименной оси координат до плоскости, образованной другими осями координат. Длина берется со знаком минус, если точка находится со стороны отрицательных значений шкалы координат. Определяет точку в пространстве при помощи радиуса r, угла азимута φ, и высоты z. Высота z соответствует координате z в прямоугольной системе координат. Радиус r - всегда неотрицательное число, задающее минимальное расстояние от точки в пространстве до оси z.show(c, aspect_ratio=1) выполнит то же самое. Сохранить
картинку можно с помощью c. 3),(x,0,2*pi),rgbcolor=hue(0.6))
sage: show(p1+p2+p3, axes=false)
3),(x,0,2*pi),rgbcolor=hue(0.6))
sage: show(p1+p2+p3, axes=false) polygon для
построения фигуры с границами, образованными заданными точками. К
примеру, создадим зеленый дельтоид:sage: L = [[-1+cos(pi*i/100)*(1+cos(pi*i/100)),
....: 2*sin(pi*i/100)*(1-cos(pi*i/100))] for i in range(200)]
sage: p = polygon(L, rgbcolor=(1/8,3/4,1/2))
sage: p
Graphics object consisting of 1 graphics primitive
show(p, axes=false), чтобы не показывать осей на графике.sage: L = [[6*cos(pi*i/100)+5*cos((6/2)*pi*i/100),
....: 6*sin(pi*i/100)-5*sin((6/2)*pi*i/100)] for i in range(200)]
sage: p = polygon(L, rgbcolor=(1/8,1/4,1/2))
sage: t = text("hypotrochoid", (5,4), rgbcolor=(1,0,0))
sage: show(p+t)
 е. график функции \(y=\sin(x)\)
для \(x\) между \(-2\pi\) и \(2\pi\), перевернутый по
отношению к линии в 45 градусов. Следующая команда Sage построит
вышеуказанное:
е. график функции \(y=\sin(x)\)
для \(x\) между \(-2\pi\) и \(2\pi\), перевернутый по
отношению к линии в 45 градусов. Следующая команда Sage построит
вышеуказанное:sage: v = [(sin(x),x) for x in srange(-2*float(pi),2*float(pi),0.1)]
sage: line(v)
Graphics object consisting of 1 graphics primitive
sage: v = [(tan(x),x) for x in srange(-2*float(pi),2*float(pi),0.01)]
sage: show(line(v), xmin=-20, xmax=20)
sage: f = lambda x,y: cos(x*y)
sage: contour_plot(f, (-4, 4), (-4, 4))
Graphics object consisting of 1 graphics primitive
Трехмерные графики

Онлайн калькулятор: Системы координат в пространстве
Прямоугольная, цилиндрическая и сферическая системы координатПрямоугольная система координат
Цилндрическая система координат
 Азимутальный угол φ - значение в диапазоне 0 ..360 градусов - определяет угол, между положительной полуосью x и радиусом, проложенным через проекцию точки на плоскость, образованную осями x и y.
Азимутальный угол φ - значение в диапазоне 0 ..360 градусов - определяет угол, между положительной полуосью x и радиусом, проложенным через проекцию точки на плоскость, образованную осями x и y.Сферическая система координат
Прямоугольные координаты в пространстве
Точность вычисленияЗнаков после запятой: 2
Цилиндрические координаты
Азимут (φ), градусы
Сферические координаты
Азимут (φ), градусы
Полярный угол (θ), градусы
content_copy Ссылка save Сохранить extension Виджет
Формулы преобразования декартовых координат
Радиус в цилиндрической системе:
Радиус в сферической системе:
Азимут:
, см Арктангенс с двумя аргументами
Полярный угол:
Цилиндрические координаты
Точность вычисленияЗнаков после запятой: 2
Прямоугольные координаты
Сферические координаты
Азимут (φ), градусы
Полярный угол (θ), градусы
content_copy Ссылка save Сохранить extension Виджет
Формулы преобразования цилиндрических координат
Декартовы координаты:
,
Радиус в сферической системе:
Полярный угол:
, см Арктангенс с двумя аргументами
Сферические координаты
Точность вычисленияЗнаков после запятой: 2
Прямоугольные координаты
Цилиндрические координаты
Азимут (φ), градусы
content_copy Ссылка save Сохранить extension Виджет
Формулы преобразования сферических координат
Декартовы координаты:
,
,
Радиус в цилиндрической системе:
Онлайн калькуляторы, расчеты и формулы на GELEOT.
 RU
RUВекторы представляют собой особый раздел аналитической геометрии, который в том числе оказал значительное влияние на развитие физики. Сам по себе вектор выглядит как отрезок, который имеет начало и имеет конец, определен заданной конечными точками длиной этого отрезка. Но внутри вектора кроется множество других скрытых функций, за счет того что вектор задает направление. Поэтому если для отрезка не имеет значения какая точка названа началом, а какая концом, и чаще просто применяется принцип чтения «слева направо», то для векторов AB и BA – это диаметрально противоположные понятия.
Итак, в векторе присутствует две важных составляющих – это его длина и направление. Тем не менее, координатами вектора задается не его фактическая длина, а местоположение на плоскости или в пространстве. Поэтому длина вектора, иначе называемая модуль вектора, вычисляется, используя прямоугольный треугольник с осями координат. Дальнейшие действия с вектором также чаще используют именно его координаты, нежели фактическую длину. Работе с векторами можно провести аналогию с целыми числами, - как только появляются отрицательные числа на числовой оси, приходится не только считать значение примера, но и все время обращать внимание на знаки. Так и с векторами, во всех действиях – будь то сложение, вычитание, умножение скалярное или векторное и другие действия, приходится не только учитывать реальные масштабы вектора – координаты, длина или угол, но и принимать в расчет его направление. К слову, направления векторов также находят отражение в знаках – обратный изначальному вектор всегда будет со знаком «минус».
Работе с векторами можно провести аналогию с целыми числами, - как только появляются отрицательные числа на числовой оси, приходится не только считать значение примера, но и все время обращать внимание на знаки. Так и с векторами, во всех действиях – будь то сложение, вычитание, умножение скалярное или векторное и другие действия, приходится не только учитывать реальные масштабы вектора – координаты, длина или угол, но и принимать в расчет его направление. К слову, направления векторов также находят отражение в знаках – обратный изначальному вектор всегда будет со знаком «минус».
В данном разделе разложены все основные действия с векторами, такие как нахождение длины вектора, координат вектора, сложение векторов, вычитание векторов, скалярное произведение векторов, векторное произведение векторов, смешанное произведение трех векторов, вычисление угла между векторами и другие. Все расчет можно произвести для векторов на плоскости или для векторов в пространстве. Также доступен векторный калькулятор, который вычисляет все возможные параметры одного и более векторов, с заданными координатами точек вектора.
Пузырьковая диаграмма (Bubble Chart)
Большинство из тех, кто хоть раз строил графики в Microsoft Excel или PowerPoint, замечали необычный и забавный тип диаграмм - пузырьковые (bubble chart). Многие видели их в чужих файлах или презентациях. Однако, в 99 случаев из 100, при попытке самостоятельно построить такую диаграмму впервые, пользователи сталкиваются с рядом неочевидных сложностей. Обычно Excel или отказывается ее создавать вообще, или создает, но совершенно непонятного вида, без подписей и наглядности.
Давайте разберемся в этой теме.
Что такое пузырьковая диаграмма
Пузырьковая диаграмма - это специфический тип диаграмм, способных отображать трехмерные данные в двумерном пространстве. Рассмотрим для примера вот такую диаграмму, отображающую статистику по странам с известного сайта-конструктора диаграмм http://www.gapminder.org/ :
Скачать полноразмерный PDF можно отсюда http://www.gapminder.org/downloads/gapminder-world-map/
По горизонтальной оси Х откладывается средний годовой доход на душу населения в USD. По вертикальной оси Y откладывается средняя продолжительность жизни в годах. Размер же (диаметр или площадь) каждого пузырька пропорционален населению каждой страны. Таким образом, на одной плоской диаграмме удается отобразить трехмерную информацию.
По вертикальной оси Y откладывается средняя продолжительность жизни в годах. Размер же (диаметр или площадь) каждого пузырька пропорционален населению каждой страны. Таким образом, на одной плоской диаграмме удается отобразить трехмерную информацию.
Дополнительную информационную нагрузку несет еще и цвет, отображающий региональную принадлежность каждой страны к определенному континенту.
Как построить пузырьковую диаграмму в Excel
Самый важный момент при построении пузырьковой диаграммы - правильно подготовленная таблица с исходными данными. А именно - таблица должна состоять строго из трех столбцов в следующем порядке (слева-направо):
- Параметр для откладывания по оси Х
- Параметр для откладывания по оси Y
- Параметр, определяющий размер пузырька
Возьмем для примера вот такую таблицу с данными по игровым приставкам:
Чтобы построить по ней пузырьковую диаграмму, нужно выделить диапазон C3:E8 (строго - только оранжевые и серые ячейки без столбца с названиями) и затем:
- В Excel 2007/2010 - перейти на вкладку Вставка - группа Диаграммы - Другие - Пузырьковая (Insert - Chart - Bubble)
- В Excel 2003 и старше - выбрать в меню Вставка - Диаграмма - Пузырьковая (Insert - Chart - Bubble)
Получившаяся в итоге диаграмма будет отображать быстродействие приставок по оси X, число программ для них по оси Y и долю рынка, занимаемого каждой приставкой - как размер пузырька:
После создания пузырьковой диаграммы имеет смысл настроить подписи к осям - без названий осей трудно понять, что по какой из них откладывается. В Excel 2007/2010 это можно сделать на вкладке Макет (Layout), а в старых версиях Excel - щелкнув по диаграмме правой кнопкой мыши и выбрав команду Параметры диаграммы (Chart options) - вкладка Заголовки (Titles).
В Excel 2007/2010 это можно сделать на вкладке Макет (Layout), а в старых версиях Excel - щелкнув по диаграмме правой кнопкой мыши и выбрав команду Параметры диаграммы (Chart options) - вкладка Заголовки (Titles).
К сожалению, Excel не позволяет автоматически привязывать цвет пузырьков к исходным данным (как в примере выше со странами), но для наглядности можно быстро отформатировать все пузырьки в разные цвета. Для этого щелкните правой кнопкой мыши на любом пузырьке, выберите команду Формат ряда данных (Format series) из контекстного меню и включите опцию Разноцветные точки (Vary colors).
Проблема с подписями
Общей трудностью, с которой сталкиваются абсолютно все пользователи при построении пузырьковых (и точечных, кстати, тоже) диаграмм, являются подписи к пузырькам. Стандартными средствами Excel можно вывести в качестве подписей только значения X, Y, размер пузырька или называние ряда (общее для всех). Если вспомнить что при построении пузырьковой диаграммы вы не выделяли столбец с подписями, а только три столбца с данными X, Y и размер пузырьков, то все оказывается в общем-то логично: то, что не выделено - в диаграмму само никак попасть не может.
Решить проблему подписей можно тремя путями:
Способ 1. Вручную
Вручную переименовывать (менять) подписи для каждого пузырька. Можно просто щелкнуть мышью по контейнеру с подписью и ввести с клавиатуры новое название вместо старого. Очевидно, что при большом количестве пузырьков этот способ начинает напоминать мазохизм.
Способ 2. Надстройка XYChartLabeler
Нетрудно предположить, что с подобной проблемой до нас с вами сталкивались и другие пользователи Excel. И один из них, а именно легендарный Rob Bovey (дай бог ему здоровья) написал и выложил в открытый доступ бесплатную надстройку XYChartLabeler, добавляющую в Excel эту недостающую функцию.
Скачать надстройку можно здесь http://appspro.com/Utilities/ChartLabeler.htm
После установки у вас появится новая вкладка (в старых версиях Excel - панель инструментов) XY Chart Labels:
Выделив пузырьки и воспользовавшись кнопкой Add Labels можно быстро и удобно добавить подписи сразу ко всем пузырькам в диаграмме, просто задав диапазон ячеек с текстом для подписей:
Способ 3. Excel 2013
Excel 2013
В новой версии Microsoft Excel 2013 появилась наконец-таки возможность добавлять подписи к элементам данных диаграммы из любых произвольно выделенных ячеек. Дождались 🙂
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространствеВыберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.
Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости.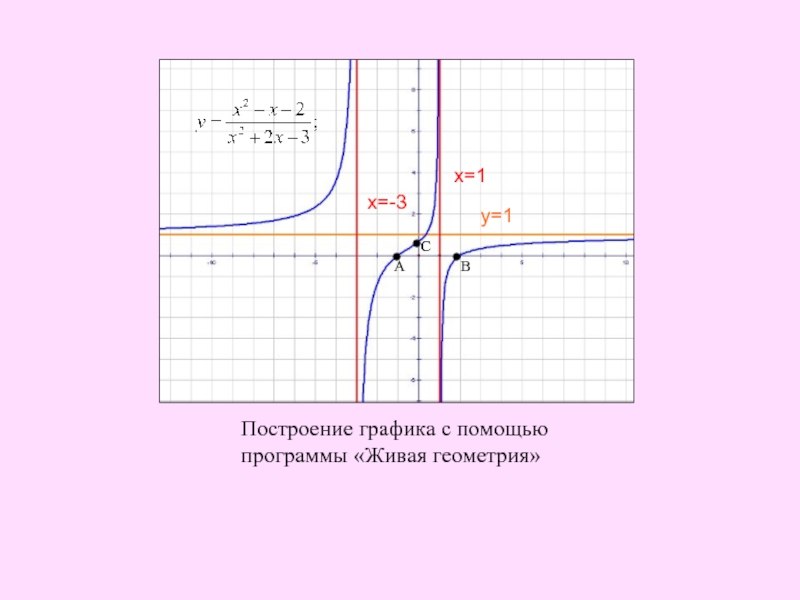 Только координат не две, а три. Возьмем векторы и .
Только координат не две, а три. Возьмем векторы и .
Сумма векторов:
Разность векторов:
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и :
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму:
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и , а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
Для точки M:
То есть A + C + D = 0.
Для точки N:
Аналогично для точки K:
Получили систему из трех уравнений:
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
Выразим C и B через A и подставим в третье уравнение:
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Упростим систему:
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать "параллелепипед".
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Итак, AA1 = √3
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.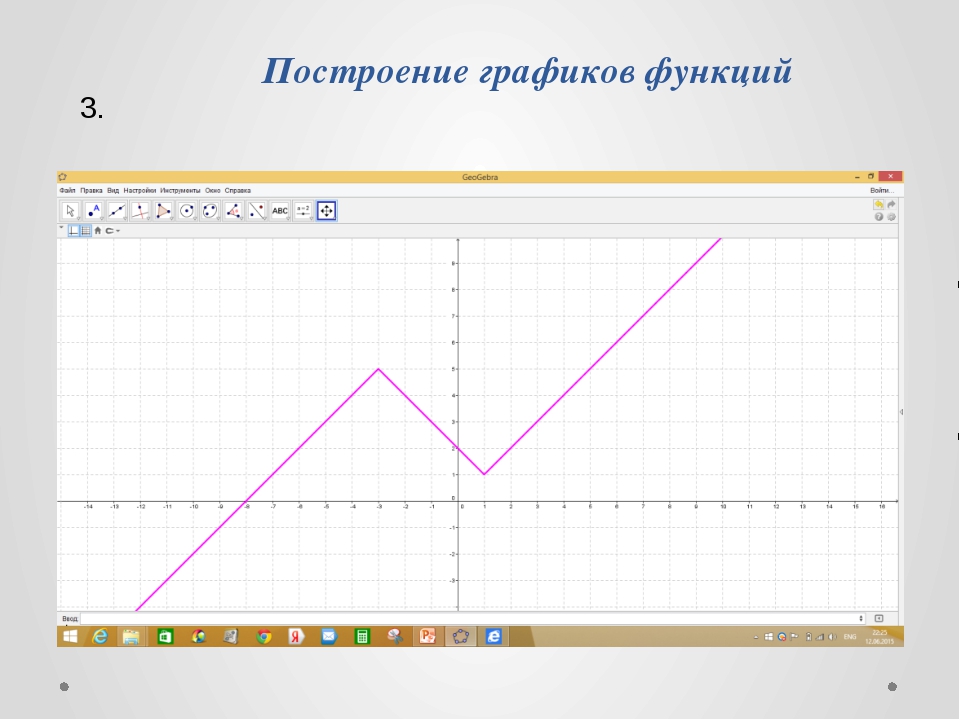
Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7.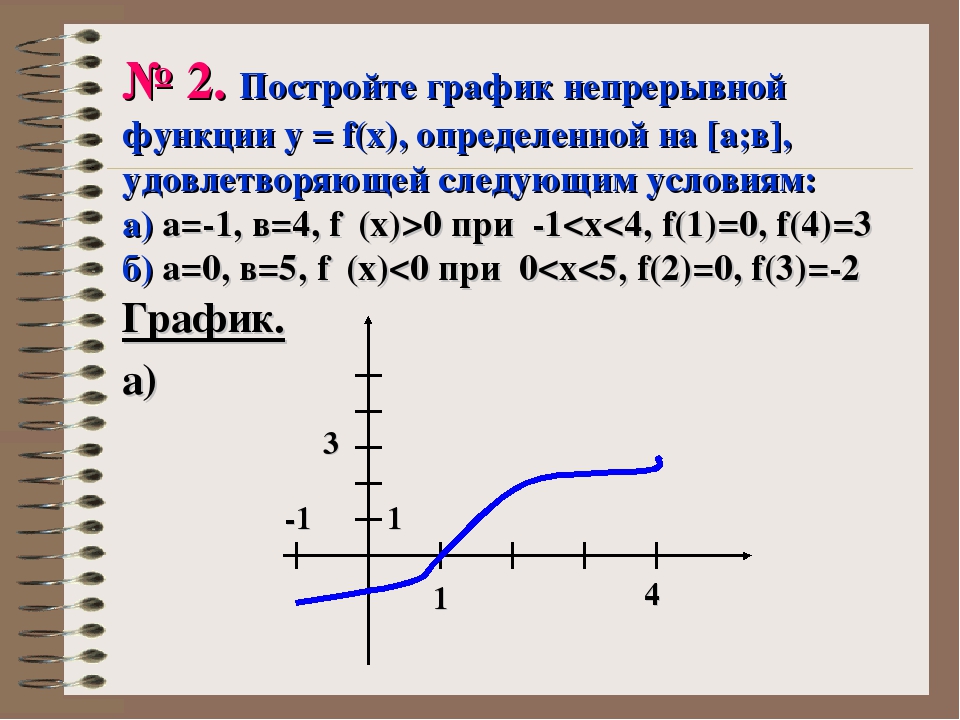 В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA1 = . Найдите расстояние от точки A до плоскости A1DB.
В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA1 = . Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Линия пересечения плоскостей онлайн
С помощю этого онлайн калькулятора можно найти линию пересечения плоскостей. Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку "Решить". Теоретическую часть и численные примеры смотрите ниже.
Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку "Решить". Теоретическую часть и численные примеры смотрите ниже.
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Линия пересечения плоскостей − теория, примеры и решения
Две плоскости в пространстве могут быть параллельными, могут совпадать или пересекаться. В данной статье мы определим взаимное расположение двух плоскостей, и если эти плоскости пересекаются, выведем уравнение линии пересечения плоскостей.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы плоскости α1 и α2:
| α1: A1x+B1y+C1z+D1=0, | (1) |
| α2: A2x+B2y+C2z+D2=0, | (2) |
где n1={A1, B1, C1} и n2={A2, B2, C2} − нормальные векторы плоскостей α1 и α2, соответственно.
Найдем уравнение линии пересеченя плоскостей α1 и α2. Для этого рассмотрим следующие случаи:
1. Нормальные векторы n1 и n2 плоскостей α1 и α2 коллинеарны (Рис.1).
Поскольку векторы n1 и n2 коллинеарны, то существует такое число λ≠0, что выполнено равенство n1=λn2, т.е. A1=λA2, B1=λB2, C1=λC2.
Умножив уравнение (2) на λ, получим:
| α2: A1x+B1y+C1z+λD2=0, | (3) |
Если выполненио равенство D1=λD2, то плоскости α1 и α2 совпадают, если же D1≠λD2то плоскости α1 и α2 параллельны, то есть не пересекаются.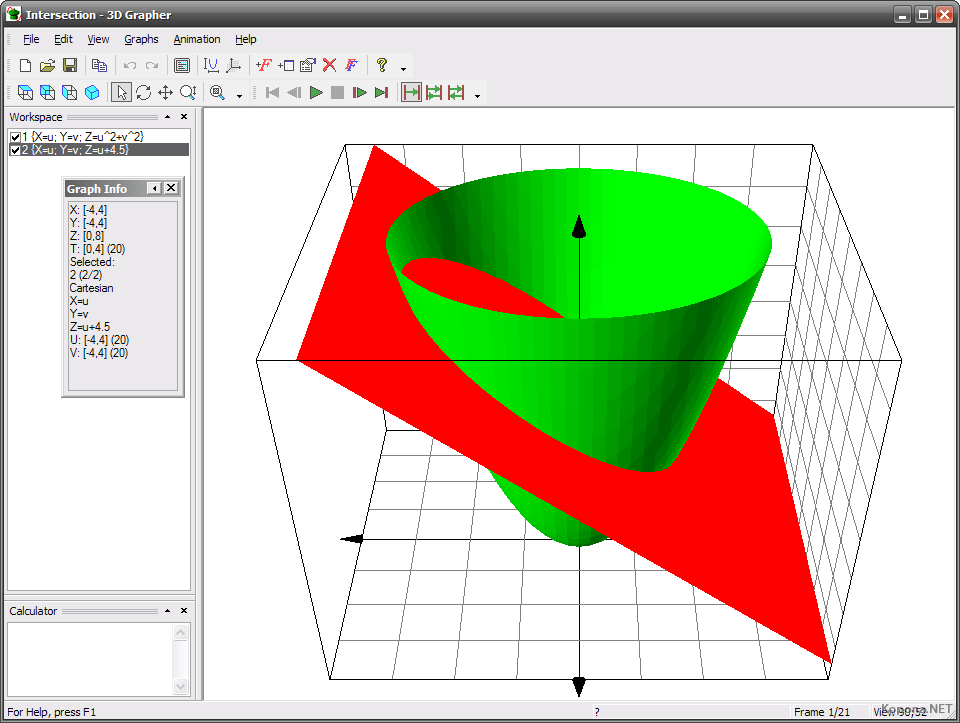
2. Нормальные векторы n1 и n2 плоскостей α1 и α2 не коллинеарны (Рис.2).
Если векторы n1 и n2 не коллинеарны, то решим систему линейных уравнений (1) и (2). Для этого переведем свободные члены на правую сторону уравнений и составим соответствующее матричное уравнение:
Как решить уравнение (4) посмотрите на странице Метод Гаусса онлайн или Метод Жоржана-Гаусса онлайн.
Так как в системе линейных уравнений (4) векторы n1={A1, B1, C1} и n2={A2, B2, C2} не коллинеарны, то решение этой системы линейных уравнений имеет следующий вид:
где x0, y0, z0, m, p, l действительные числа, а t − переменная.
Равенство (5) можно записать в следующем виде:
Мы получили параметрическое уравнение прямой, которое является линией пересечения плоскостей α1 и α2.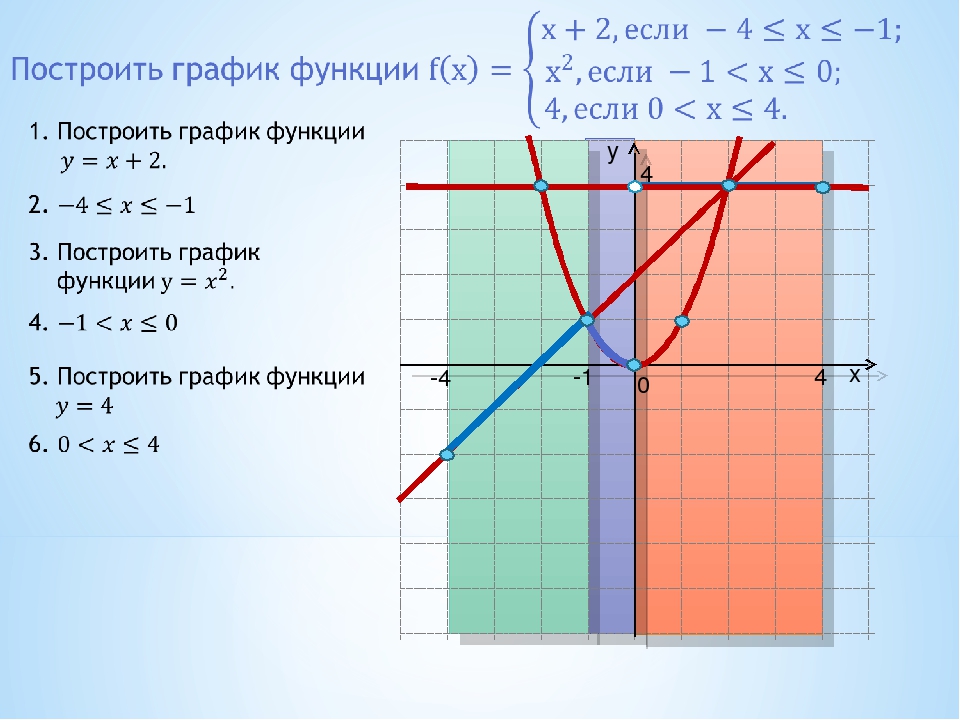 Полученное уравнение прямой можно записать в каноническом виде:
Полученное уравнение прямой можно записать в каноническом виде:
Пример 1. Найти линию пересечения плоскостей α1 и α2:
Решение. Определим, сначала, взаимное расположение данных плоскостей. Плоскость α1 имеет нормальный вектор n1={A1, B1, C1}={1, 2, 1}. Плоскость α2 имеет нормальный вектор n2={A2, B2, C2}={2, 9, −5}.
Поскольку направляющие векторы n1 и n2 неколлинеарны, то плолскости α1 и α2 пересекаются.
Для нахождения линии пересечения влоскостей α1 и α2 нужно решить систему линейных уравнений (7) и (8). Для этого составим матричное уравнение этой системы:
Решим систему линейных уравнений (9) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 2 со строкой 1, умноженной на −2:
Второй этап. Обратный ход Гаусса.
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на −2/5:
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
Получим решение:
где t− произвольное действительное число.
Запишем (11) в следующем виде:
Получили уравнение линии пересечения плоскостей α1 и α2 в параметрическом виде. Запишем ее в каноническом виде.
Из равентсв выше получим каноническое уравнение прямой:
Ответ. Уравнение линии пересечения плоскостей α1 и α2имеет вид:
Пример 2. Найти линию пересечения плоскостей α1 и α2:
Решение.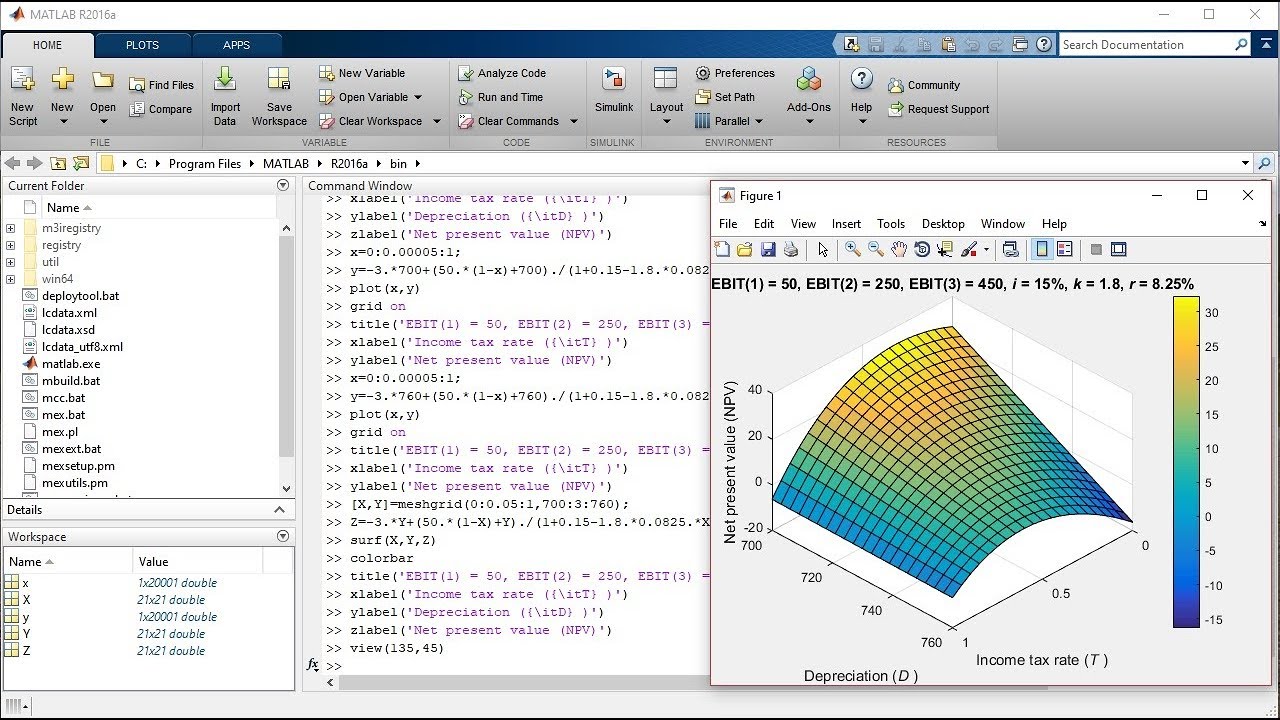 Определим, сначала, взаимное расположение данных плоскостей. Плоскость α1 имеет нормальный вектор n1={A1, B1, C1}={1, 2, 7}. Плоскость α2 имеет нормальный вектор n2={A2, B2, C2}={2, 4, 14}.
Определим, сначала, взаимное расположение данных плоскостей. Плоскость α1 имеет нормальный вектор n1={A1, B1, C1}={1, 2, 7}. Плоскость α2 имеет нормальный вектор n2={A2, B2, C2}={2, 4, 14}.
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/2), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/2:
Так как нормальные векторы уравнений (14) и (16) совпадают, а свободные члены разные, то плоскости α1 и α2 не совпадают. Следовательно они параллельны, т.е. не пересекаются.
Пример 3.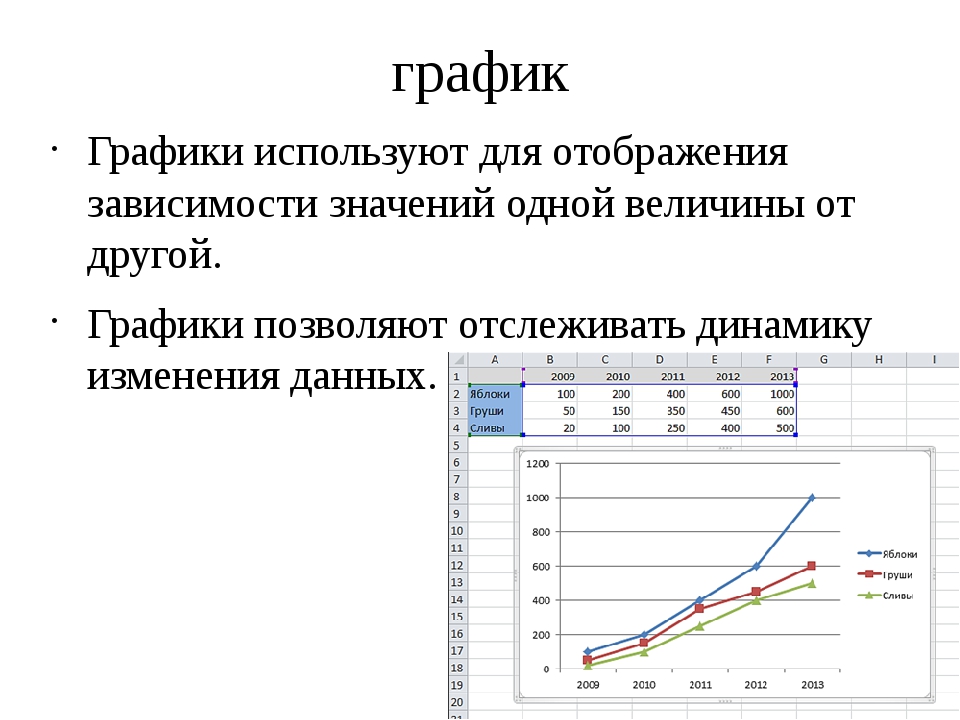 Найти линию пересечения плоскостей α1 и α2:
Найти линию пересечения плоскостей α1 и α2:
Решение. Определим, сначала, взаимное расположение данных плоскостей. Плоскость α1 имеет нормальный вектор n1={A1, B1, C1}={5, −2, 3}. Плоскость α2 имеет нормальный вектор n2={A2, B2, C2}={15, −6, 9}.
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/3), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/3:
Так как нормальные векторы уравнений (17) и (19) совпадают, и свободные члены равны, то плоскости α1 и α2 совпадают.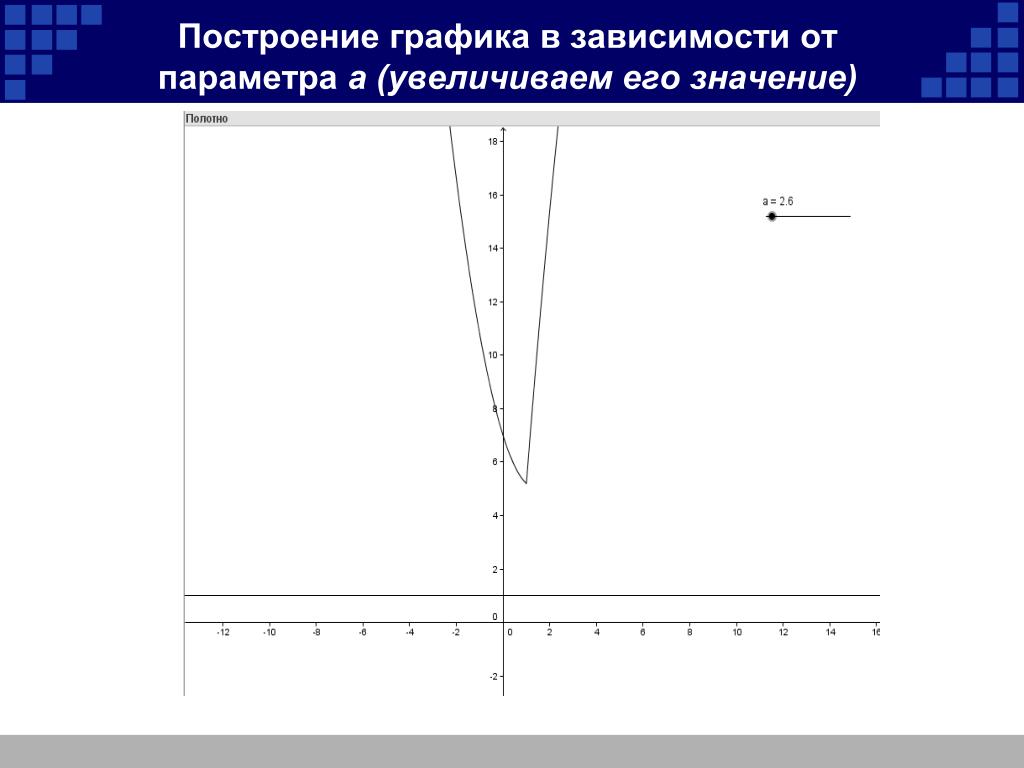
Базовое 3D-построение СводкаВ Origin можно создавать контурные и трехмерные графики, такие как графики поверхности цветовой карты, непосредственно из данных XYZ. Но, если вы хотите построить более гладкую трехмерную поверхность, вам настоятельно рекомендуется использовать одну из встроенных процедур построения координатной сетки Origin для преобразования данных XYZ в матрицу. Требуется минимальная версия Origin: Origin 9.0 SR1 Что вы узнаетеИз этого туториала Вы узнаете, как:
Создание трехмерной поверхности и точечной диаграммы
Сглаживание трехмерной поверхностиЕсли вы хотите создать трехмерную поверхность, более гладкую, чем приведенный выше график поверхности (созданный из данных XYZ), вы можете сначала преобразовать данные XYZ в матрицу с помощью инструмента XYZ Gridding . А затем используйте данные матрицы результатов для создания трехмерной поверхности.
|
Как построить диаграмму рассеяния в Excel
В этом руководстве вы узнаете, как построить диаграмму рассеяния в Excel для создания графического представления двух коррелированных наборов данных.
Что вы видите при просмотре двух столбцов количественных данных в электронной таблице Excel? Всего два набора цифр. Вы хотите увидеть, как эти два набора связаны друг с другом? Диаграмма рассеяния - идеальный выбор для этого.
Вы хотите увидеть, как эти два набора связаны друг с другом? Диаграмма рассеяния - идеальный выбор для этого.
Точечная диаграмма в Excel
Диаграмма рассеяния (также называемая диаграммой рассеяния XY или диаграммой рассеяния ) - это двухмерная диаграмма, которая показывает взаимосвязь между двумя переменными.
На точечной диаграмме и горизонтальная, и вертикальная оси представляют собой оси значений, на которых отображаются числовые данные.Обычно независимая переменная находится на оси x, а зависимая переменная - на оси y. На диаграмме отображаются значения на пересечении осей x и y, объединенные в отдельные точки данных.
Основная цель диаграммы разброса - показать, насколько сильна связь или корреляция между двумя переменными. Чем плотнее точки данных располагаются вдоль прямой линии, тем выше корреляция.
Как расположить данные для точечной диаграммы
Благодаря множеству встроенных шаблонов диаграмм, предоставляемых Excel, создание точечной диаграммы превращается в парочку щелчков мышью. Но сначала вам нужно правильно расположить исходные данные.
Но сначала вам нужно правильно расположить исходные данные.
Как уже упоминалось, точечный график отображает две взаимосвязанные количественные переменные. Итак, вы вводите два набора числовых данных в два отдельных столбца.
Для простоты использования независимая переменная должна находиться в левом столбце , так как этот столбец будет нанесен на ось x. Зависимая переменная (та, на которую влияет независимая переменная) должна находиться в правом столбце , и она будет нанесена на ось y.
Наконечник. Если ваш зависимый столбец находится перед независимым столбцом и вы не можете изменить его на листе, вы можете поменять местами оси x и y прямо на диаграмме. В нашем примере мы собираемся визуализировать взаимосвязь между рекламным бюджетом за определенный месяц (независимая переменная) и количеством проданных товаров (зависимая переменная), поэтому мы располагаем данные соответствующим образом:
Как создать диаграмму рассеяния в Excel
Если исходные данные правильно организованы, то для построения диаграммы рассеяния в Excel необходимо выполнить два быстрых шага:
- Выберите два столбца с числовыми данными, включая заголовки столбцов.
 В нашем случае это диапазон C1: D13. Не выбирайте другие столбцы, чтобы не запутать Excel.
В нашем случае это диапазон C1: D13. Не выбирайте другие столбцы, чтобы не запутать Excel. - Перейдите на вкладку Inset > группа Chats , щелкните значок диаграммы Scatter и выберите нужный шаблон. Чтобы вставить классический точечный график, щелкните первую миниатюру:
Диаграмма рассеяния будет немедленно вставлена в ваш рабочий лист:
В принципе можно считать проделанную работу. Или вы можете настроить некоторые элементы вашего графика, чтобы он выглядел более красивым и более четко передавал корреляцию между двумя переменными.
Типы точечных диаграмм
Помимо классической диаграммы рассеяния, показанной в приведенном выше примере, доступно еще несколько шаблонов:
- Scatter с плавными линиями и маркерами
- Скаттер с плавными линиями
- Скаттер с прямыми линиями и маркерами
- Скаттер с прямыми линиями
Scatter с линиями лучше всего использовать, когда у вас мало точек данных.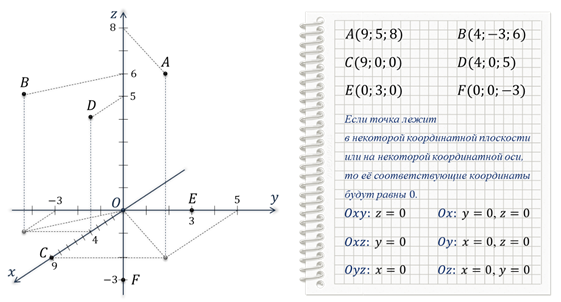 Например, вот как вы можете представить данные за первые четыре месяца с помощью диаграммы разброса с плавными линиями и маркерами:
Например, вот как вы можете представить данные за первые четыре месяца с помощью диаграммы разброса с плавными линиями и маркерами:
Шаблоны графиков Excel XY также могут рисовать каждой переменной по отдельности , представляя одни и те же отношения по-разному.Для этого следует выбрать 3 столбца с данными - крайний левый столбец с текстовыми значениями (метками) и два столбца с числами.
В нашем примере синие точки обозначают стоимость рекламы, а оранжевые точки обозначают проданные товары:
Чтобы просмотреть все доступные типы разброса в одном месте, выберите данные, щелкните значок разброс (X, Y) на ленте, а затем щелкните Дополнительные диаграммы разброса… Откроется диалоговое окно Inset Chart с выбран тип XY (Scatter) , и вы переключаетесь между различными шаблонами вверху, чтобы увидеть, какой из них обеспечивает наилучшее графическое представление ваших данных:
Трехмерная диаграмма рассеяния
В отличие от классической диаграммы рассеяния XY, трехмерная диаграмма рассеяния отображает точки данных по трем осям (x, y и z), чтобы показать взаимосвязь между тремя переменными.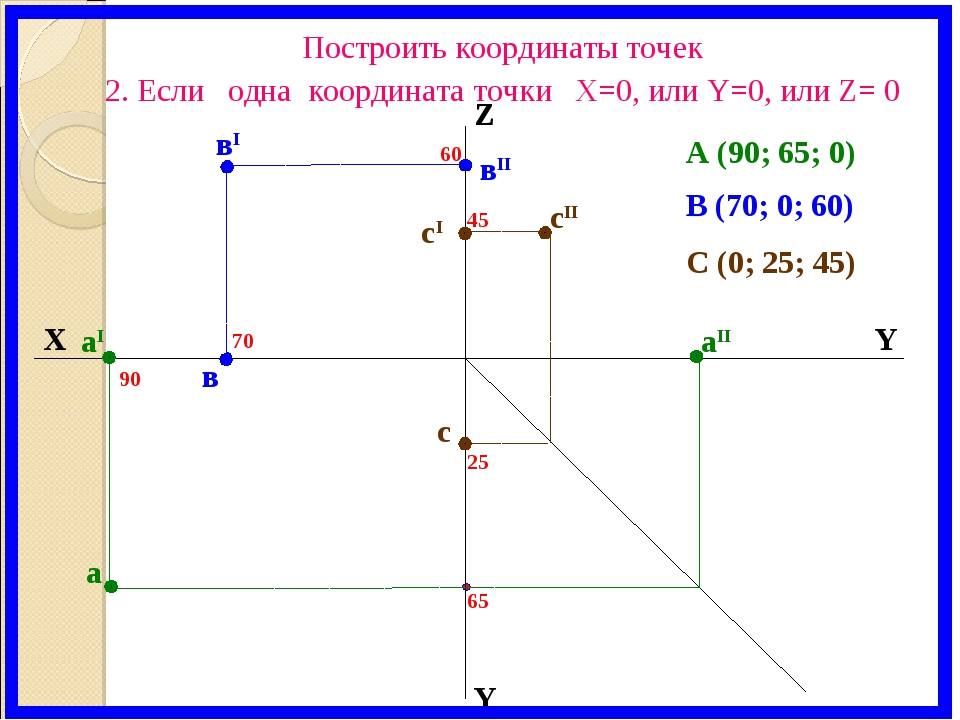 Поэтому его часто называют графиком XYZ .
Поэтому его часто называют графиком XYZ .
К сожалению, невозможно создать трехмерную диаграмму рассеяния в Excel даже в новой версии Excel 2019. Если вам очень нужен этот тип диаграммы для анализа данных, рассмотрите возможность использования стороннего инструмента, например plot.ly. На приведенном ниже снимке экрана показано, какой вид трехмерной диаграммы разброса может нарисовать этот инструмент:
Точечный график и корреляция
Чтобы правильно интерпретировать диаграмму рассеяния, необходимо понимать, как переменные могут соотноситься друг с другом.Всего существует три типа корреляции:
Положительная корреляция - по мере увеличения переменной x увеличивается и переменная y. Примером сильной положительной корреляции является количество времени, которое студенты проводят за учебой, и их оценки.
Отрицательная корреляция - по мере увеличения переменной x переменная y уменьшается. Отказ от уроков и оценок отрицательно коррелирован - по мере увеличения количества пропусков экзаменационные баллы снижаются.
Нет корреляции - нет очевидной взаимосвязи между двумя переменными; точки разбросаны по всей области диаграммы.Например, кажется, что между ростом и оценками учащихся нет никакой корреляции, поскольку первое никак не влияет на вторые.
Настройка диаграммы рассеяния XY в Excel
Как и в случае с другими типами диаграмм, почти каждый элемент точечной диаграммы в Excel можно настроить. Вы можете легко изменить заголовок диаграммы, добавить заголовки осей, скрыть линии сетки, выбрать собственные цвета диаграммы и многое другое.
Ниже мы сосредоточимся на нескольких настройках, специфичных для точечной диаграммы.
Отрегулируйте масштаб оси (уменьшите пустое пространство)
Если точки данных сгруппированы вверху, внизу, справа или слева от графика, вы можете убрать лишнее пустое пространство.
Чтобы уменьшить расстояние между первой точкой данных и вертикальной осью и / или между последней точкой данных и правым краем графика, выполните следующие действия:
- Щелкните правой кнопкой мыши по оси x и выберите Ось формата…
- На панели «Ось формата » установите требуемые границы минимум и максимум соответственно.

- Кроме того, вы можете изменить блоки Major , которые управляют интервалом между линиями сетки.
На скриншоте ниже показаны мои настройки:
Чтобы удалить пространство между точками данных и верхним / нижним краями области графика, отформатируйте вертикальную ось y аналогичным образом.
Добавить метки к точкам данных точечной диаграммы
При создании точечного графика с относительно небольшим количеством точек данных вы можете пометить точки по имени, чтобы сделать визуальное представление более понятным. Вот как это можно сделать:
- Выберите график и нажмите кнопку Элементы диаграммы .
- Отметьте поле Data Labels , щелкните маленькую черную стрелку рядом с ним, а затем щелкните Дополнительные параметры…
- На панели Format Data Labels перейдите на вкладку Label Options (последняя) и настройте метки данных следующим образом:
- Выберите поле Значение из ячеек , а затем выберите диапазон, из которого вы хотите извлечь метки данных (B2: B6 в нашем случае).

- Если вы хотите отображать только имена, снимите флажок X Value и / или Y Value , чтобы удалить числовые значения из меток.
- Укажите положение меток, В нашем примере выше точек данных.
Вот и все! Все точки данных на нашем графике рассеяния в Excel теперь помечены по имени:
Когда две или более точки данных находятся очень близко друг к другу, их метки могут перекрываться, как в случае с метками Jan и Mar на нашей диаграмме разброса. Чтобы исправить это, щелкните метки, а затем нажмите перекрывающуюся, чтобы была выбрана только эта метка.Наведите курсор мыши на выбранную метку, пока курсор не изменится на четырехстороннюю стрелку, а затем перетащите метку в желаемое положение.
В результате вы получите красивую диаграмму рассеяния в Excel с хорошо читаемыми надписями:
Добавьте линию тренда и уравнение
Чтобы лучше визуализировать взаимосвязь между двумя переменными, вы можете нарисовать линию тренда на диаграмме разброса Excel, также называемую линией наилучшего соответствия .
Для этого щелкните правой кнопкой мыши любую точку данных и выберите Добавить линию тренда… из контекстного меню.
Excel проведет линию как можно ближе ко всем точкам данных, чтобы над линией было столько точек, сколько показано ниже.
Кроме того, вы можете показать уравнение для линии тренда , которое математически описывает взаимосвязь между двумя переменными. Для этого установите флажок «Отображать уравнение на диаграмме » на панели «Линия тренда формата » , которая должна появиться в правой части окна Excel сразу после добавления линии тренда.Результат этих манипуляций будет выглядеть примерно так:
То, что вы видите на скриншоте выше, часто называют графиком линейной регрессии , и вы можете найти подробные инструкции по его созданию здесь: Как создать график линейной регрессии в Excel.
Как поменять местами оси X и Y на диаграмме рассеивания
Как уже упоминалось, диаграмма рассеяния обычно отображает независимую переменную на горизонтальной оси и зависимую переменную на вертикальной оси. Если ваш график построен по-другому, самое простое решение - поменять местами исходные столбцы на листе, а затем нарисовать диаграмму заново.
Если ваш график построен по-другому, самое простое решение - поменять местами исходные столбцы на листе, а затем нарисовать диаграмму заново.
Если по какой-либо причине переупорядочивание столбцов невозможно, вы можете переключать серии данных X и Y прямо на диаграмме. Вот как:
- Щелкните правой кнопкой мыши любую ось и выберите Выбрать данные… в контекстном меню.
- В диалоговом окне Select Data Source нажмите кнопку Edit .
- Скопируйте значения X серии в поле значений Y серии и наоборот.
Наконечник. Чтобы безопасно редактировать содержимое полей Series , поместите указатель мыши в поле и нажмите F2.
- Дважды щелкните ОК , чтобы закрыть оба окна.
В результате ваша диаграмма рассеяния Excel подвергнется следующему преобразованию:
Вот как вы создаете диаграмму рассеяния в Excel. В нашем следующем руководстве мы продолжим эту тему и покажем, как быстро найти и выделить определенную точку данных на диаграмме разброса. Пожалуйста, не переключайтесь!
Пожалуйста, не переключайтесь!
Вас также может заинтересовать
3 Визуализация данных | R для науки о данных
Введение
«Простой график предоставил аналитикам больше информации. чем любое другое устройство ». - Джон Тьюки
Эта глава научит вас визуализировать данные с помощью ggplot2. В R есть несколько систем построения графиков, но ggplot2 - одна из самых элегантных и универсальных. ggplot2 реализует грамматику графики , согласованную систему для описания и построения графиков.С ggplot2 вы можете сделать больше быстрее, изучив одну систему и применив ее во многих местах.
Если вы хотите узнать больше о теоретических основах ggplot2, прежде чем начать, я бы рекомендовал прочитать «Многослойная грамматика графики», http://vita.had.co.nz/papers/layered-grammar. pdf.
Предпосылки
В этой главе основное внимание уделяется ggplot2, одному из основных членов тидиверсии. Чтобы получить доступ к наборам данных, страницам справки и функциям, которые мы будем использовать в этой главе, загрузите тидиверс, запустив этот код:
Чтобы получить доступ к наборам данных, страницам справки и функциям, которые мы будем использовать в этой главе, загрузите тидиверс, запустив этот код:
Библиотека (tidyverse)
#> ── Присоединение пакетов ──────────────────────────────────────── tidyverse 1.3.0 ──
#> ✔ ggplot2 3.3.2 ✔ мурлыкать 0.3.4
#> ✔ tibble 3.0.3 ✔ dplyr 1.0.2
#> ✔ тидыр 1.1.2 ✔ стрингер 1.4.0
#> ✔ readr 1.4.0 ✔ forcats 0.5.0
#> ── Конфликты ─────────────────────────────────────────── tidyverse_conflicts () ──
#> ✖ dplyr :: filter () маскирует stats :: filter ()
#> ✖ dplyr :: lag () маски stats :: lag () Эта одна строка кода загружает основной тидиверс; пакеты, которые вы будете использовать практически при каждом анализе данных. Он также сообщает вам, какие функции из тидиверса конфликтуют с функциями в базовом R (или из других пакетов, которые вы могли загрузить).
Если вы запустите этот код и получите сообщение об ошибке «нет пакета с именем« tidyverse »», вам нужно сначала установить его, а затем снова запустить library () .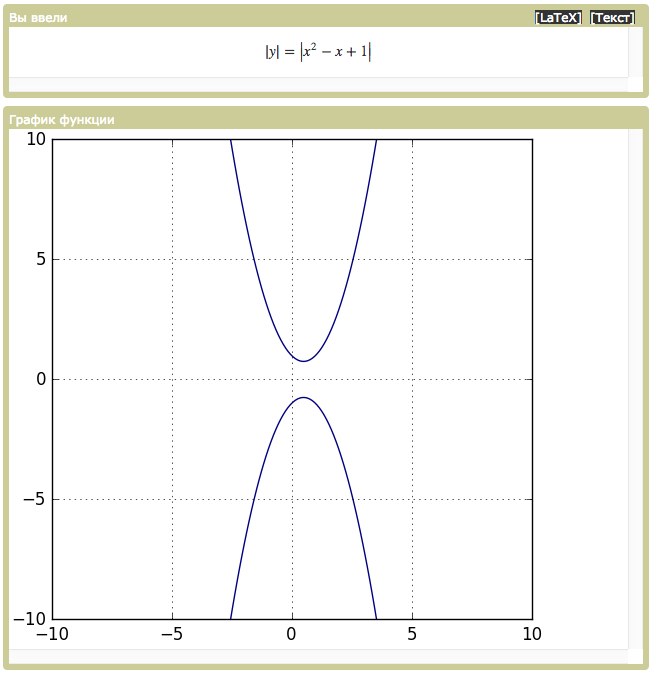
Вам нужно установить пакет только один раз, но вам нужно перезагружать его каждый раз, когда вы начинаете новый сеанс.
Если нам нужно точно указать, откуда взялась функция (или набор данных), мы воспользуемся специальной формой package :: function () . Например, ggplot2 :: ggplot () явно сообщает вам, что мы используем функцию ggplot () из пакета ggplot2.
Первые шаги
Давайте воспользуемся нашим первым графиком, чтобы ответить на вопрос: автомобили с большими двигателями потребляют больше топлива, чем автомобили с маленькими двигателями? Вероятно, у вас уже есть ответ, но постарайтесь дать точный ответ. Как выглядит взаимосвязь между объемом двигателя и топливной экономичностью? Это положительно? Отрицательный? Линейный? Нелинейный?
Фрейм данных
миль на галлон Вы можете проверить свой ответ с помощью фрейма данных mpg , найденного в ggplot2 (он же ggplot2 :: mpg ). Фрейм данных представляет собой прямоугольную коллекцию переменных (в столбцах) и наблюдений (в строках).
Фрейм данных представляет собой прямоугольную коллекцию переменных (в столбцах) и наблюдений (в строках). миль на галлон содержит наблюдения, собранные Агентством по охране окружающей среды США на 38 моделях автомобилей.
миль на галлон
#> # Таблица: 234 x 11
#> модель производителя displ год cyl trans drv cty hwy fl class
#>
#> 1 audi a4 1.8 1999 4 авто (l5) f 18 29 p компа…
#> 2 audi a4 1.8 1999 4 механика (m5) f 21 29 p compa…
#> 3 audi a4 2 2008 4 механика (m6) f 20 31 p compa…
#> 4 audi a4 2 2008 4 auto (av) f 21 30 p compa…
#> 5 audi a4 2.8 1999 6 auto (l5) f 16 26 p compa…
#> 6 audi a4 2.8 1999 6 механика (m5) f 18 26 p compa…
#> #… С еще 228 строками Среди переменных в миль на галлон следующие:
displ- объем двигателя автомобиля в литрах.hwy, топливная экономичность автомобиля на шоссе, в милях на галлон (миль на галлон). Автомобиль с низкой топливной экономичностью потребляет больше топлива, чем автомобиль с высокой топливной экономичностью.
топливная экономичность, когда они едут на одинаковое расстояние.
Автомобиль с низкой топливной экономичностью потребляет больше топлива, чем автомобиль с высокой топливной экономичностью.
топливная экономичность, когда они едут на одинаковое расстояние.
Чтобы узнать больше о миль на галлон , откройте страницу справки, запустив ? Mpg .
Создание ggplot
Чтобы построить миль на галлон , запустите этот код, чтобы поместить displ на ось x и hwy на ось y:
ggplot (данные = миль на галлон) +
geom_point (отображение = aes (x = displ, y = hwy)) График показывает отрицательную зависимость между объемом двигателя ( displ ) и топливной экономичностью ( hwy ).Другими словами, автомобили с большими двигателями потребляют больше топлива. Подтверждает или опровергает это вашу гипотезу о топливной экономичности и объеме двигателя?
С помощью ggplot2 вы начинаете построение графика с помощью функции ggplot () .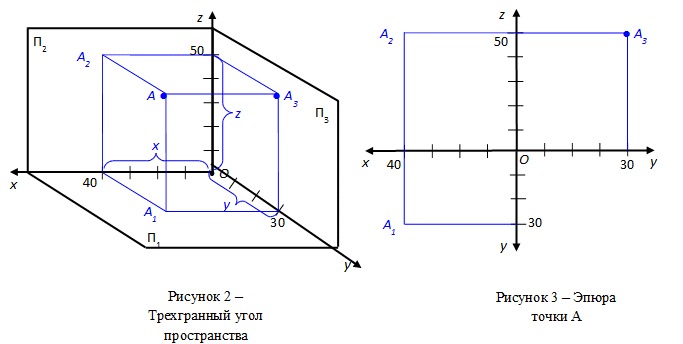
ggplot () создает систему координат, в которую вы можете добавлять слои. Первый аргумент ggplot () - это набор данных для использования в графике. Итак, ggplot (data = mpg) создает пустой график, но это не очень интересно, поэтому я не собираюсь его здесь показывать.
Вы завершаете свой график, добавляя один или несколько слоев в ggplot () . Функция geom_point () добавляет слой точек к вашему графику, который создает диаграмму рассеяния. ggplot2 поставляется с множеством функций geom, каждая из которых добавляет к графику разные типы слоев. В этой главе вы узнаете о них целую кучу.
Каждая функция geom в ggplot2 принимает аргумент сопоставления . Это определяет, как переменные в вашем наборе данных сопоставляются с визуальными свойствами.Аргумент сопоставления всегда связан с aes () , а аргументы x и y aes () указывают, какие переменные сопоставлять с осями x и y.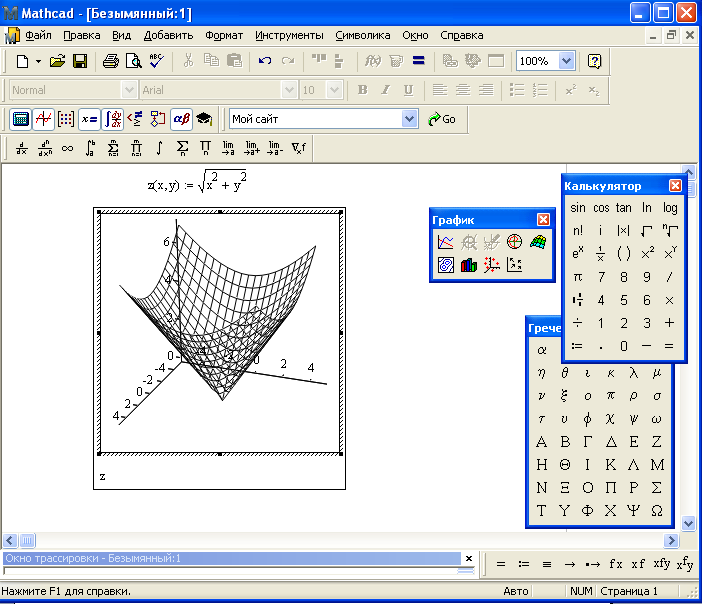 ggplot2 ищет отображаемые переменные в аргументе
ggplot2 ищет отображаемые переменные в аргументе data , в данном случае миль на галлон .
Графический шаблон
Давайте превратим этот код в шаблон многократного использования для построения графиков с помощью ggplot2. Чтобы построить график, замените заключенные в скобки разделы в приведенном ниже коде набором данных, функцией geom или набором сопоставлений.
ggplot (data = ) +
(отображение = aes ()) В оставшейся части этой главы вы узнаете, как дополнить и расширить этот шаблон для создания различных типов графиков. Начнем с компонента .
Упражнения
Run
ggplot (data = mpg). Что ты видишь?Сколько строк в милях на галлон ? Сколько столбцов?
Что описывает переменная
drv? Прочтите справку для?миль на галлон, чтобы найти из.
Создайте диаграмму рассеяния
hwyиcyl.Что произойдет, если вы построите диаграмму рассеяния
classvsdrv? Почему сюжет не полезен?
Эстетические карты
«Самая большая ценность картины — это когда она заставляет нас замечать то, что мы никогда не ожидал увидеть. — Джон Тьюки
На графике ниже одна группа точек (выделена красным), кажется, выходит за пределы линейного тренда.Эти автомобили имеют больший пробег, чем можно было ожидать. Как вы можете объяснить эти машины?
Предположим, что автомобили — гибриды. Один из способов проверить эту гипотезу — посмотреть на значение класса для каждого автомобиля. Переменная class набора данных миль на галлон классифицирует автомобили по таким группам, как компактные, среднеразмерные и внедорожники. Если отдаленные точки являются гибридами, их следует классифицировать как компактные или, возможно, малолитражные автомобили (имейте в виду, что эти данные были собраны до того, как гибридные грузовики и внедорожники стали популярными).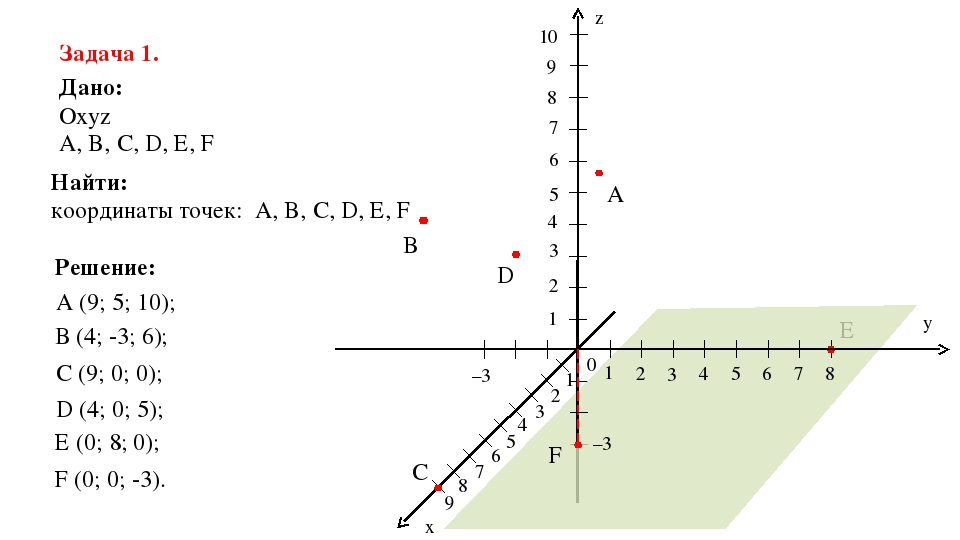
Вы можете добавить третью переменную, например class , к двумерной диаграмме рассеяния, сопоставив ее с эстетикой . Эстетика — это визуальное свойство объектов на вашем участке. Эстетика включает такие вещи, как размер, форма или цвет ваших очков. Вы можете отображать точку (как показано ниже) по-разному, изменяя значения ее эстетических свойств. Поскольку мы уже используем слово «значение» для описания данных, давайте использовать слово «уровень» для описания эстетических свойств.Здесь мы меняем уровни размера, формы и цвета точки, чтобы сделать точку маленькой, треугольной или синей:
Вы можете передать информацию о своих данных, сопоставив эстетику графика с переменными в наборе данных. Например, вы можете сопоставить цвета ваших точек с переменной class , чтобы показать класс каждой машины.
ggplot (данные = миль на галлон) +
geom_point (отображение = aes (x = displ, y = hwy, color = class)) (Если вы предпочитаете британский английский, например Hadley, вы можете использовать цвета вместо цвета .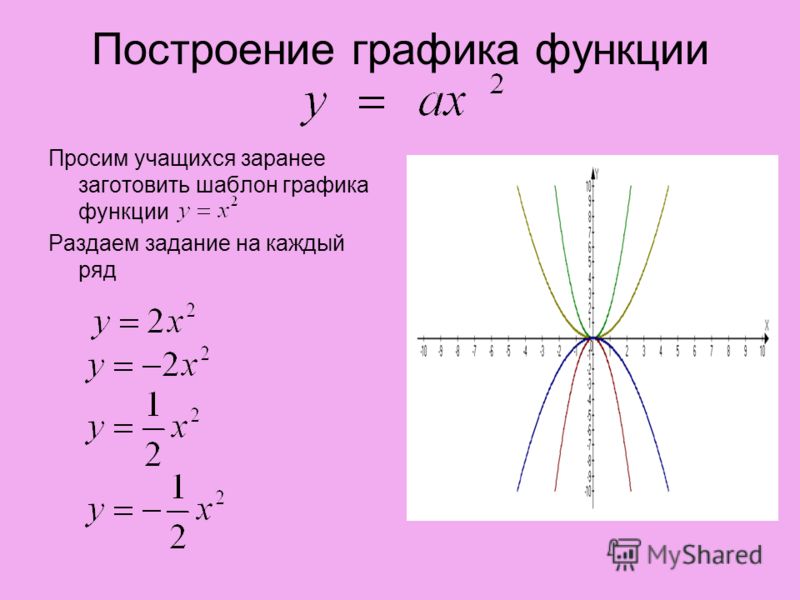 )
)
Чтобы сопоставить эстетику переменной, свяжите имя эстетики с именем переменной внутри aes () . ggplot2 автоматически присвоит уникальный уровень эстетики (здесь уникальный цвет) каждому уникальному значению переменной, процесс, известный как масштабирование . ggplot2 также добавит легенду, объясняющую, какие уровни каким значениям соответствуют.
По цветам видно, что многие из необычных вещей представляют собой двухместные автомобили. Эти автомобили не похожи на гибриды, а на самом деле являются спортивными автомобилями! Спортивные автомобили имеют большие двигатели, такие как внедорожники и пикапы, но маленькие кузова, такие как автомобили среднего и компактного размера, что позволяет сократить расход топлива.Оглядываясь назад, эти автомобили вряд ли были гибридами, поскольку у них были большие двигатели.
В приведенном выше примере мы сопоставили класс с эстетикой цвета, но мы могли бы сопоставить класс с эстетикой размера таким же образом.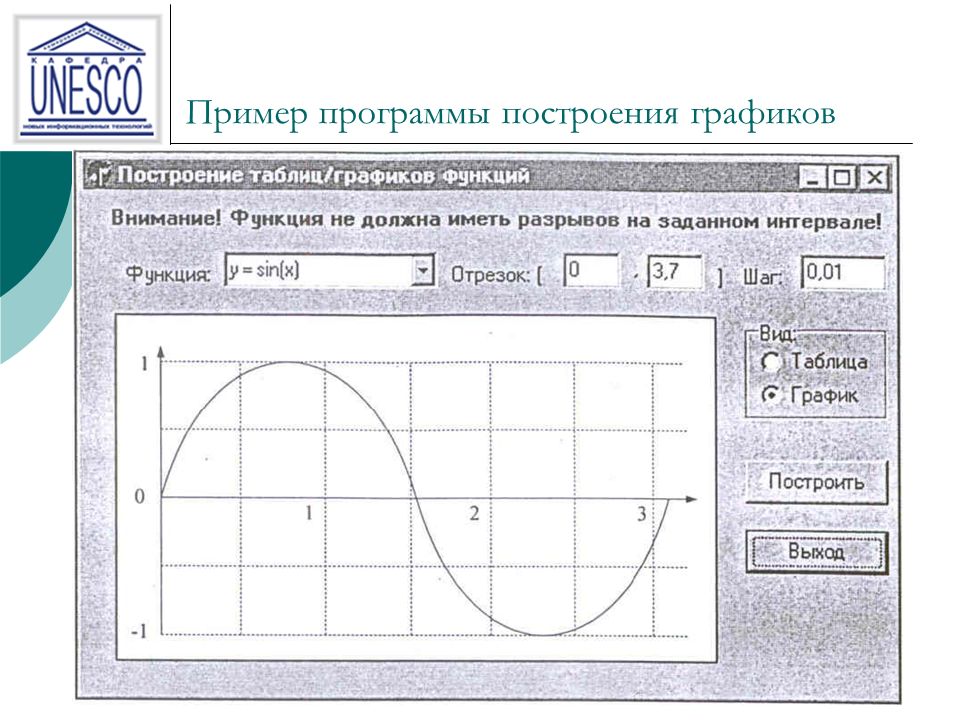 В этом случае точный размер каждой точки покажет ее классовую принадлежность. Здесь мы получаем предупреждение , потому что сопоставление неупорядоченной переменной (
В этом случае точный размер каждой точки покажет ее классовую принадлежность. Здесь мы получаем предупреждение , потому что сопоставление неупорядоченной переменной (, класс ) с упорядоченной эстетикой ( размер ) не является хорошей идеей.
ggplot (данные = миль на галлон) +
geom_point (отображение = aes (x = displ, y = hwy, size = class))
#> Предупреждение: не рекомендуется использовать размер дискретной переменной. Или мы могли бы сопоставить класс с эстетикой alpha , которая контролирует прозрачность точек, или с эстетикой формы, которая управляет формой точек.
# слева
ggplot (данные = миль на галлон) +
geom_point (отображение = aes (x = displ, y = hwy, alpha = class))
# Правильно
ggplot (данные = миль на галлон) +
geom_point (отображение = aes (x = displ, y = hwy, shape = class)) Что случилось с внедорожниками? ggplot2 будет использовать одновременно только шесть фигур.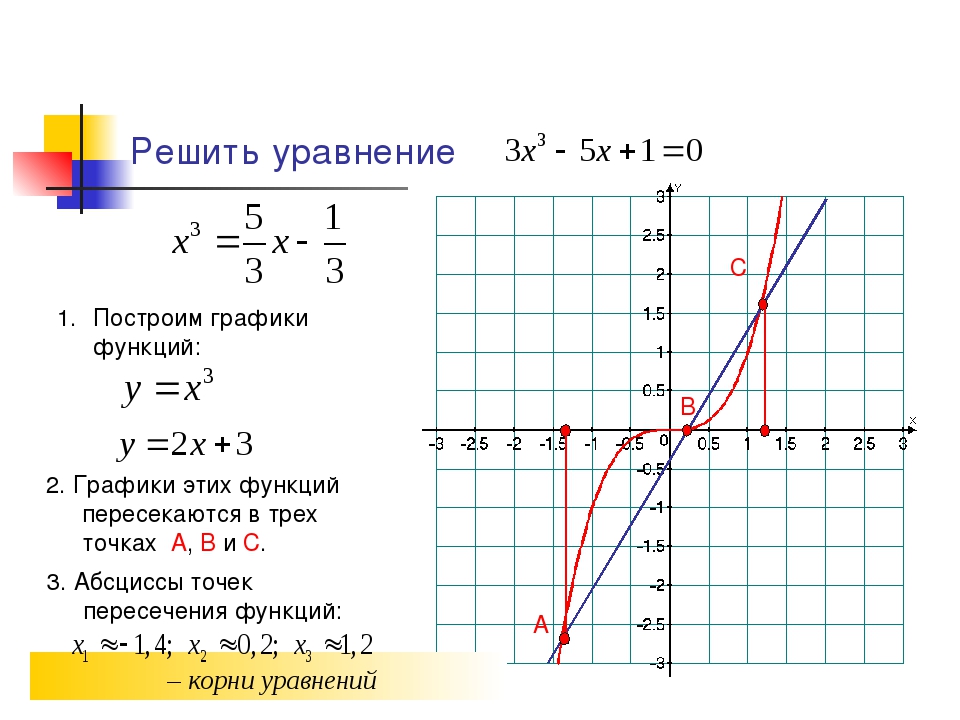 По умолчанию при использовании эстетики формы дополнительные группы не отображаются.
По умолчанию при использовании эстетики формы дополнительные группы не отображаются.
Для каждой эстетики вы используете aes () , чтобы связать имя эстетики с отображаемой переменной. Функция aes () собирает вместе все эстетические сопоставления, используемые слоем, и передает их аргументу сопоставления слоя. Синтаксис подчеркивает полезную информацию о x и y : положения x и y точки сами по себе являются эстетикой, визуальными свойствами, которые вы можете сопоставить с переменными для отображения информации о данных.
После того, как вы нанесете на карту эстетику, ggplot2 позаботится обо всем остальном. Он выбирает разумный масштаб для использования с эстетикой и строит легенду, объясняющую соответствие между уровнями и значениями. Для эстетики x и y ggplot2 не создает легенду, но создает осевую линию с делениями и меткой. Линия оси действует как легенда; он объясняет соответствие между местоположениями и ценностями.
Вы также можете установить эстетические свойства геометрии вручную.Например, мы можем сделать все точки на нашем графике синими:
ggplot (данные = миль на галлон) +
geom_point (mapping = aes (x = displ, y = hwy), color = "blue") Здесь цвет не передает информацию о переменной, а только изменяет внешний вид графика. Чтобы установить эстетику вручную, задайте эстетику по имени в качестве аргумента вашей функции geom; то есть идет за пределы из aes () . Вам нужно будет выбрать уровень, соответствующий этой эстетике:
Имя цвета в виде строки символов.
Размер точки в мм.
Форма точки в виде числа, как показано на Рисунке 3.1.
Рисунок 3.1: R имеет 25 встроенных форм, которые обозначены номерами. Есть некоторые кажущиеся дубликаты: например, 0, 15 и 22 — все квадраты. Разница заключается во взаимодействии цвета и заливки эстетики .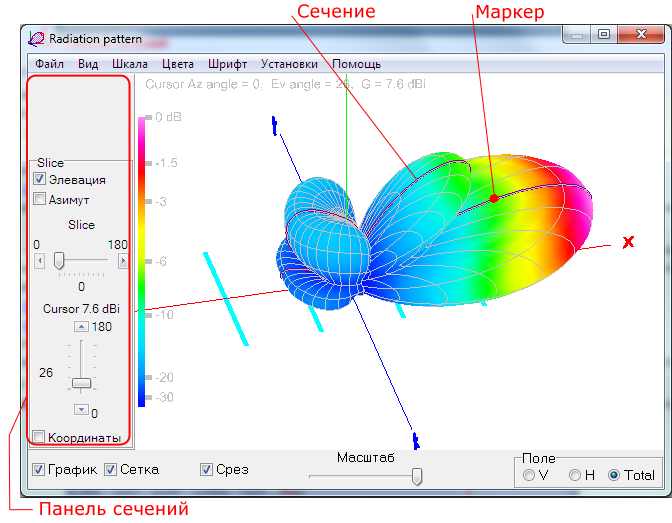 Полые формы (0–14) имеют границу, определяемую цветом
Полые формы (0–14) имеют границу, определяемую цветом ; сплошные фигуры (15–20) залиты цветом цвета ; закрашенные фигуры (21–24) имеют границу цвета и заполнены заливкой .
Упражнения
Что случилось с этим кодом? Почему точки не синие?
ggplot (данные = миль на галлон) + geom_point (mapping = aes (x = displ, y = hwy, color = "blue"))Какие переменные в
миль на галлонявляются категориальными? Какие переменные непрерывны? (Подсказка: введите? Mpg, чтобы прочитать документацию по набору данных). Как Вы можете увидеть эту информацию, когда запуститемиль на галлон?Сопоставьте непрерывную переменную с
цветом,размеромиформой.Как делать эти эстетики ведут себя по-разному для категориального и непрерывного переменные?Что произойдет, если сопоставить одну и ту же переменную с несколькими эстетиками?
Что делает эстетика
stroke? С какими формами он работает? (Подсказка: используйте? Geom_point)Что произойдет, если вы сопоставите эстетику с чем-то другим, кроме переменной имя, например
aes (color = displ <5)? Обратите внимание: вам также необходимо указать x и y.
Общие проблемы
При запуске кода R вы, вероятно, столкнетесь с проблемами. Не волнуйтесь - это случается со всеми. Я писал код на R в течение многих лет, и каждый день я все еще пишу код, который не работает!
Начните с тщательного сравнения кода, который вы запускаете, с кодом в книге. R чрезвычайно разборчив, и неуместный персонаж может иметь решающее значение. Убедитесь, что каждые ( соответствует ) и каждые дюймов сопряжены с другим дюймов .Иногда вы запускаете код, но ничего не происходит. Посмотрите на левую часть консоли: если это + , это означает, что R не думает, что вы набрали полное выражение, и ждет, когда вы его закончите. В этом случае обычно легко снова начать с нуля, нажав ESCAPE, чтобы прервать обработку текущей команды.
Одна из распространенных проблем при создании графики ggplot2 - поставить + в неправильное место: он должен стоять в конце строки, а не в начале.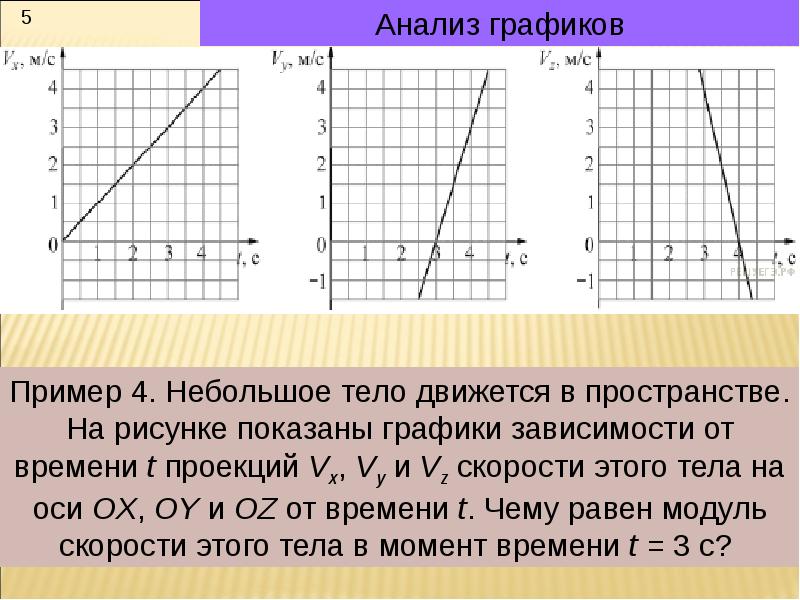 Другими словами, убедитесь, что вы случайно не написали такой код:
Другими словами, убедитесь, что вы случайно не написали такой код:
ggplot (данные = миль на галлон)
+ geom_point (отображение = aes (x = displ, y = hwy)) Если вы все еще не знаете, что делать, попробуйте помощь. Вы можете получить справку по любой функции R, запустив ? Имя_функции в консоли или выбрав имя функции и нажав F1 в RStudio. Не волнуйтесь, если помощь не покажется такой полезной - вместо этого перейдите к примерам и поищите код, соответствующий тому, что вы пытаетесь сделать.
Если это не помогло, внимательно прочтите сообщение об ошибке. Иногда там и закопают ответ! Но когда вы новичок в R, ответ может быть в сообщении об ошибке, но вы еще не знаете, как это понять. Еще один отличный инструмент - Google: попробуйте поискать в Google сообщение об ошибке, так как, вероятно, кто-то другой столкнулся с такой же проблемой и получил помощь в Интернете.
Грани
Один из способов добавить дополнительные переменные - это эстетика. Другой способ, особенно полезный для категориальных переменных, - разделить график на фасетов , подзаголовки, каждый из которых отображает одно подмножество данных.
Другой способ, особенно полезный для категориальных переменных, - разделить график на фасетов , подзаголовки, каждый из которых отображает одно подмножество данных.
Чтобы огранить ваш график одной переменной, используйте facet_wrap () . Первым аргументом facet_wrap () должна быть формула, которую вы создаете с ~ , за которой следует имя переменной (здесь «формула» - это имя структуры данных в R, а не синоним «уравнения»). Переменная, которую вы передаете в facet_wrap () , должна быть дискретной.
ggplot (данные = миль на галлон) +
geom_point (отображение = aes (x = displ, y = hwy)) +
facet_wrap (~ класс, nrow = 2) Чтобы обработать график на основе комбинации двух переменных, добавьте facet_grid () к вызову графика.Первый аргумент facet_grid () также является формулой. На этот раз формула должна содержать два имени переменных, разделенных символами ~ .
ggplot (данные = миль на галлон) +
geom_point (отображение = aes (x = displ, y = hwy)) +
facet_grid (DRV ~ Cyl) Если вы предпочитаете не фасетировать измерение строк или столбцов, используйте . вместо имени переменной, например + facet_grid (. ~ Цил) .
Упражнения
Что произойдет, если вы фасетите непрерывную переменную?
Что означают пустые ячейки на графике с
facet_grid (drv ~ cyl)? Как они относятся к этому сюжету?ggplot (данные = миль на галлон) + geom_point (отображение = aes (x = drv, y = cyl))Какие графики создает следующий код? Что значит
.делать?ggplot (данные = миль на галлон) + geom_point (отображение = aes (x = displ, y = hwy)) + facet_grid (drv ~.) ggplot (данные = миль на галлон) + geom_point (отображение = aes (x = displ, y = hwy)) + facet_grid (. ~ cyl)
~ cyl) Возьмите первый граненый график в этом разделе:
ggplot (данные = миль на галлон) + geom_point (отображение = aes (x = displ, y = hwy)) + facet_wrap (~ класс, nrow = 2)Каковы преимущества использования огранки вместо эстетики цвета? Какие недостатки? Как мог бы измениться баланс, если бы у вас был больший набор данных?
Прочитать
? Facet_wrap.Что делаетnrow? Что делаетncol? Какие еще варианты управления компоновкой отдельных панелей? Почему неfacet_grid ()имеет аргументыnrowиncol?При использовании
facet_grid ()вы обычно должны помещать переменную с большим количеством уникальные уровни в столбцах. Почему?
Геометрические объекты
Чем похожи эти два сюжета?
Оба графика содержат одну и ту же переменную x, одну и ту же переменную y, и оба описывают одни и те же данные. Но сюжеты не идентичны. Каждый график использует разные визуальные объекты для представления данных. В синтаксисе ggplot2 мы говорим, что они используют разные геометрии .
Но сюжеты не идентичны. Каждый график использует разные визуальные объекты для представления данных. В синтаксисе ggplot2 мы говорим, что они используют разные геометрии .
A geom - это геометрический объект, который график использует для представления данных. Люди часто описывают сюжеты по типу геометрии, которую они используют. Например, гистограммы используют геометрию гистограмм, линейные диаграммы используют геометрию линий, коробчатые диаграммы используют геометрию прямоугольной диаграммы и так далее. Диаграммы рассеяния ломают тренд; они используют точечную геометрию. Как мы видим выше, вы можете использовать разные геометрии для построения одних и тех же данных.График слева использует точечную геометрию, а график справа использует гладкую геометрию, плавную линию, подогнанную к данным.
Чтобы изменить геометрию на вашем графике, измените функцию geom, которую вы добавляете к ggplot () . Например, чтобы построить графики выше, вы можете использовать этот код:
# осталось
ggplot (данные = миль на галлон) +
geom_point (отображение = aes (x = displ, y = hwy))
# верно
ggplot (данные = миль на галлон) +
geom_smooth (отображение = aes (x = displ, y = hwy)) Каждая функция geom в ggplot2 принимает аргумент сопоставления .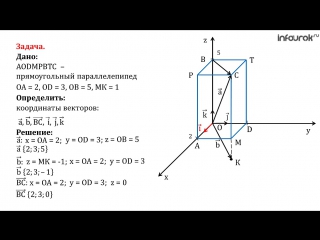 Однако не всякая эстетика подходит для всех геометрических фигур. Вы можете задать форму точки, но не можете задать «форму» линии. С другой стороны, вы можете установить тип линии.
Однако не всякая эстетика подходит для всех геометрических фигур. Вы можете задать форму точки, но не можете задать «форму» линии. С другой стороны, вы можете установить тип линии. geom_smooth () будет рисовать разные линии с разными типами линий для каждого уникального значения переменной, которую вы сопоставляете с типом линии.
ggplot (данные = миль на галлон) +
geom_smooth (отображение = aes (x = displ, y = hwy, linetype = drv)) Здесь geom_smooth () разделяет автомобили на три строки на основе их значения drv , которое описывает трансмиссию автомобиля.Одна линия описывает все точки со значением 4 , одна линия описывает все точки со значением f , а одна линия описывает все точки со значением r . Здесь 4 обозначает полный привод, f - передний привод и r - задний привод.
Если это звучит странно, мы можем сделать это более понятным, наложив линии поверх необработанных данных, а затем раскрасив все в соответствии с drv .
Обратите внимание, что этот график содержит две геометрии на одном графике! Если это вас возбуждает, пристегнитесь. Очень скоро мы узнаем, как разместить несколько геометрических фигур на одном участке.
ggplot2 предоставляет более 40 геометрий, а пакеты расширений предоставляют еще больше (см. Https://exts.ggplot2.tidyverse.org/gallery/ для выборки). Лучший способ получить исчерпывающий обзор - это шпаргалка по ggplot2, которую вы можете найти по адресу http://rstudio.com/resources/cheatsheets. Чтобы узнать больше о любом отдельном geom, используйте help: ? Geom_smooth .
Многие geom, например geom_smooth () , используют один геометрический объект для отображения нескольких строк данных. Для этих геометрических фигур вы можете установить для группы эстетику категориальной переменной для рисования нескольких объектов. ggplot2 будет рисовать отдельный объект для каждого уникального значения группирующей переменной. На практике ggplot2 автоматически группирует данные для этих геометрических фигур всякий раз, когда вы сопоставляете эстетику с дискретной переменной (как в примере с типом линий ). На эту особенность удобно полагаться, потому что эстетика группы сама по себе не добавляет к геометрии легенды или отличительных особенностей.
На эту особенность удобно полагаться, потому что эстетика группы сама по себе не добавляет к геометрии легенды или отличительных особенностей.
ggplot (данные = миль на галлон) +
geom_smooth (отображение = aes (x = displ, y = hwy))
ggplot (данные = миль на галлон) +
geom_smooth (отображение = aes (x = displ, y = hwy, group = drv))
ggplot (данные = миль на галлон) +
geom_smooth (
отображение = aes (x = displ, y = hwy, color = drv),
show.legend = ЛОЖЬ
) Чтобы отобразить несколько геометрий на одном графике, добавьте несколько функций геометрии в ggplot () :
ggplot (данные = миль на галлон) +
geom_point (отображение = aes (x = displ, y = hwy)) +
geom_smooth (отображение = aes (x = displ, y = hwy)) Однако это приводит к некоторому дублированию в нашем коде.Представьте, что вы хотите изменить ось Y, чтобы отобразить cty вместо hwy .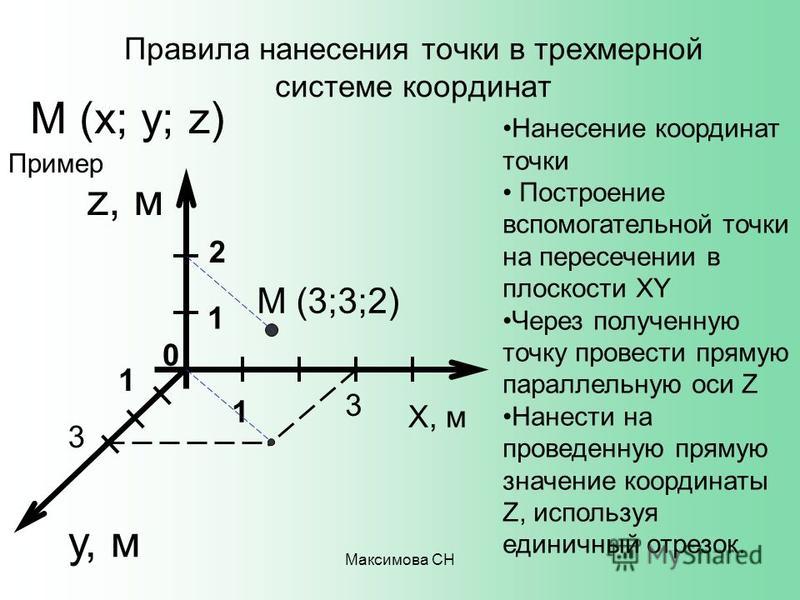 Вам нужно будет изменить переменную в двух местах, и вы можете забыть обновить одно. Вы можете избежать такого повторения, передав набор сопоставлений в
Вам нужно будет изменить переменную в двух местах, и вы можете забыть обновить одно. Вы можете избежать такого повторения, передав набор сопоставлений в ggplot () . ggplot2 будет рассматривать эти сопоставления как глобальные сопоставления, которые применяются к каждому объекту geom в графе. Другими словами, этот код создаст тот же график, что и предыдущий код:
ggplot (данные = миль на галлон, отображение = aes (x = displ, y = hwy)) +
geom_point () +
geom_smooth () Если вы разместите сопоставления в функции geom, ggplot2 будет рассматривать их как локальные сопоставления для слоя.Он будет использовать эти сопоставления для расширения или перезаписи глобальных сопоставлений только для этого уровня . Это позволяет отображать разную эстетику на разных слоях.
ggplot (данные = миль на галлон, отображение = aes (x = displ, y = hwy)) +
geom_point (отображение = aes (цвет = класс)) +
geom_smooth () Вы можете использовать ту же идею, чтобы указать разные данные для каждого слоя. Здесь наша плавная линия отображает только подмножество набора данных на
Здесь наша плавная линия отображает только подмножество набора данных на миль на галлон, субкомпактные автомобили.Аргумент локальных данных в geom_smooth () переопределяет аргумент глобальных данных в ggplot () только для этого слоя.
ggplot (данные = миль на галлон, отображение = aes (x = displ, y = hwy)) +
geom_point (отображение = aes (цвет = класс)) +
geom_smooth (data = filter (mpg, class == "subcompact"), se = FALSE) (Вы узнаете, как работает фильтр () , в главе о преобразовании данных: пока просто знайте, что эта команда выбирает только малолитражные автомобили.)
Упражнения
Какую геометрию вы бы использовали для построения линейной диаграммы? Коробчатый сюжет? Гистограмма? Диаграмма с областями?
Запустите этот код в уме и предскажите, как будет выглядеть результат. Затем запустите код на R и проверьте свои прогнозы.
ggplot (data = mpg, mapping = aes (x = displ, y = hwy, color = drv)) + geom_point () + geom_smooth (se = FALSE)Что означает
show.? Что будет, если его убрать? legend = FALSE
legend = FALSE
Как вы думаете, почему я использовал его ранее в этой главе?Что делает аргумент
seдляgeom_smooth ()?Эти два графика будут выглядеть по-разному? Почему, почему нет?
ggplot (данные = миль на галлон, отображение = aes (x = displ, y = hwy)) + geom_point () + geom_smooth () ggplot () + geom_point (данные = миль на галлон, отображение = aes (x = displ, y = hwy)) + geom_smooth (данные = миль на галлон, отображение = aes (x = displ, y = hwy))Восстановите код R, необходимый для создания следующих графиков.
Статистические преобразования
Теперь давайте взглянем на гистограмму. Гистограммы кажутся простыми, но они интересны, потому что раскрывают что-то тонкое в графиках. Рассмотрим простую гистограмму, нарисованную с помощью geom_bar () . На следующей диаграмме показано общее количество алмазов в наборе данных
На следующей диаграмме показано общее количество алмазов в наборе данных алмазов , сгруппированных по огранкам . Набор данных алмазов входит в ggplot2 и содержит информацию о ~ 54000 алмазах, включая по цене , карат , цвет , чистоты и огранки каждого алмаза.Таблица показывает, что доступно больше алмазов с огранкой высокого качества, чем с огранкой низкого качества.
ggplot (данные = бриллианты) +
geom_bar (отображение = aes (x = вырезано)) По оси x на диаграмме отображается огранки , переменная из бриллиантов . По оси Y отображается количество, но количество не является переменной в бриллиантах ! Откуда берется счет? Многие графики, например диаграммы рассеяния, отображают необработанные значения вашего набора данных. Другие графики, такие как гистограммы, вычисляют новые значения для построения:
гистограммы, гистограммы и частотные полигоны объединяют ваши данные а затем нанесите на график количество точек, которые попадают в каждую ячейку.

сглаживания подбирают модель к вашим данным, а затем строят прогнозы на основе модель.
- Коробчатые диаграммы
вычисляют надежную сводку распределения, а затем отображают специально отформатированный ящик.
Алгоритм, используемый для вычисления новых значений для графика, называется stat , сокращенно от статистического преобразования. На рисунке ниже показано, как этот процесс работает с geom_bar () .
Вы можете узнать, какой стат использует geom, проверив значение по умолчанию для аргумента stat .Например, ? Geom_bar показывает, что значением по умолчанию для stat является «count», что означает, что geom_bar () использует stat_count () . stat_count () задокументирован на той же странице, что и geom_bar () , и если вы прокрутите вниз, вы найдете раздел под названием «Вычисляемые переменные». Это описывает, как он вычисляет две новые переменные:
Это описывает, как он вычисляет две новые переменные: count и prop .
Обычно вы можете использовать геометрию и статистику как взаимозаменяемые.Например, вы можете воссоздать предыдущий график, используя stat_count () вместо geom_bar () :
ggplot (данные = бриллианты) +
stat_count (mapping = aes (x = cut)) Это работает, потому что у каждой геометрии есть стат по умолчанию; и каждый стат имеет геометрию по умолчанию. Это означает, что вы обычно можете использовать геометрию, не беспокоясь о лежащей в основе статистической трансформации. Есть три причины, по которым вам может потребоваться явное использование статистики:
Вы можете изменить статистику по умолчанию.В приведенном ниже коде я меняю статистика
geom_bar ()от счетчика (по умолчанию) до идентификатора. Это позволяет Я сопоставляю высоту столбцов с необработанными значениями переменной \ (y \). К сожалению, когда люди небрежно говорят о гистограммах, они могут
относится к этому типу столбчатой диаграммы, где высота столбца уже равна
присутствует в данных, или на предыдущей гистограмме, где высота столбца
генерируется путем подсчета строк.
К сожалению, когда люди небрежно говорят о гистограммах, они могут
относится к этому типу столбчатой диаграммы, где высота столбца уже равна
присутствует в данных, или на предыдущей гистограмме, где высота столбца
генерируется путем подсчета строк.демо <- tribble ( ~ вырезать, ~ частота, «Ярмарка», 1610 г., г. «Хорошо», 4906, г. «Очень хорошо», 12082, г. «Премиум», 13791, г. «Идеал», 21551 ) ggplot (данные = демонстрация) + geom_bar (mapping = aes (x = cut, y = freq), stat = "identity")(Не беспокойтесь, что вы раньше не видели
<-илиtribble ().Вы, возможно уметь угадывать их значение из контекста, и вы точно узнаете что они скоро сделают!)Вы можете захотеть переопределить отображение по умолчанию из преобразованных переменных эстетике. Например, вы можете отобразить гистограмму пропорция, а не количество:
ggplot (данные = бриллианты) + geom_bar (mapping = aes (x = cut, y = stat (prop), group = 1))Чтобы найти переменные, вычисляемые с помощью статистики, обратитесь к разделу справки.
 под названием «вычисляемые переменные».
под названием «вычисляемые переменные».Возможно, вы захотите привлечь больше внимания к статистическому преобразованию в вашем коде. Например, вы можете использовать
stat_summary (), который суммирует значения y для каждого уникального значения x, чтобы нарисовать Обратите внимание на сводку, которую вы вычисляете:ggplot (данные = бриллианты) + stat_summary ( отображение = aes (x = вырез, y = глубина), fun.min = min, fun.max = max, веселье = медиана )
ggplot2 предоставляет вам более 20 статистических данных.Каждая статистика - это функция, поэтому вы можете получить помощь обычным способом, например ? Stat_bin . Чтобы увидеть полный список статистики, попробуйте шпаргалку ggplot2.
Упражнения
Какой geom по умолчанию связан с
stat_summary ()? Как мог вы переписываете предыдущий график, чтобы использовать эту функцию geom вместо stat функция?Что делает
geom_col ()? Чем он отличается отgeom_bar ()?Большинство геометрических фигур и статистики попадают в пары, которые почти всегда используются в концерт.
 Прочтите документацию и составьте список всех
пары. Что у них общего?
Прочтите документацию и составьте список всех
пары. Что у них общего?Какие переменные вычисляет
stat_smooth ()? Какие параметры контролируют его поведение?В нашей линейчатой диаграмме пропорций нам нужно установить
group = 1. Почему? В другом словами в чем проблема с этими двумя графиками?ggplot (данные = бриллианты) + geom_bar (mapping = aes (x = cut, y = after_stat (prop))) ggplot (данные = бриллианты) + geom_bar (mapping = aes (x = вырезать, fill = color, y = after_stat (prop)))
Регулировка положения
Есть еще одно волшебство, связанное с гистограммами.Вы можете раскрасить гистограмму, используя либо эстетику , цвет , либо, что более полезно, заливку :
ggplot (данные = бриллианты) +
geom_bar (отображение = aes (x = вырезать, цвет = вырезать))
ggplot (данные = бриллианты) +
geom_bar (отображение = aes (x = вырезать, заполнить = вырезать)) Обратите внимание, что произойдет, если вы сопоставите эстетику заливки с другой переменной, например с четкостью , : полосы автоматически складываются. Каждый цветной прямоугольник представляет собой комбинацию
Каждый цветной прямоугольник представляет собой комбинацию огранки и чистоты .
ggplot (данные = бриллианты) +
geom_bar (mapping = aes (x = вырезать, заполнить = четкость)) Укладка выполняется автоматически с помощью регулировки положения , заданной аргументом позиция . Если вам не нужна столбчатая диаграмма с накоплением, вы можете использовать один из трех других вариантов: "identity" , "dodge" или "fill" .
position = "identity"разместит каждый объект именно там, где он падает. контекст графика.Это не очень полезно для баров, потому что перекрывает их. Чтобы увидеть это перекрытие, нам нужно сделать полосы слегка прозрачным, установивalphaна малое значение, или полностью прозрачный, установивfill = NA.ggplot (данные = ромбы, отображение = aes (x = вырезка, заливка = чистота)) + geom_bar (альфа = 1/5, позиция = "идентичность") ggplot (данные = бриллианты, отображение = aes (x = огранка, цвет = чистота)) + geom_bar (fill = NA, position = "identity")Регулировка положения идентичности более полезна для двухмерных геометрических фигур, таких как точки, где это значение по умолчанию.

position = "fill"работает как наложение, но делает каждый набор наборных полос такой же высоты. Это упрощает сравнение пропорций между группы.ggplot (данные = бриллианты) + geom_bar (mapping = aes (x = вырезать, заполнить = четкость), position = "fill")position = "dodge"помещает перекрывающиеся объекты непосредственно рядом с одним еще один. Это упрощает сравнение отдельных значений.ggplot (данные = бриллианты) + geom_bar (mapping = aes (x = вырез, заливка = четкость), position = "dodge")
Есть еще один тип корректировки, который бесполезен для гистограмм, но может быть очень полезен для диаграмм рассеяния. Вспомните нашу первую диаграмму рассеяния. Вы заметили, что на графике отображается только 126 точек, хотя в наборе данных 234 наблюдения?
Значения hwy и displ округлены, поэтому точки появляются на сетке, и многие точки перекрывают друг друга.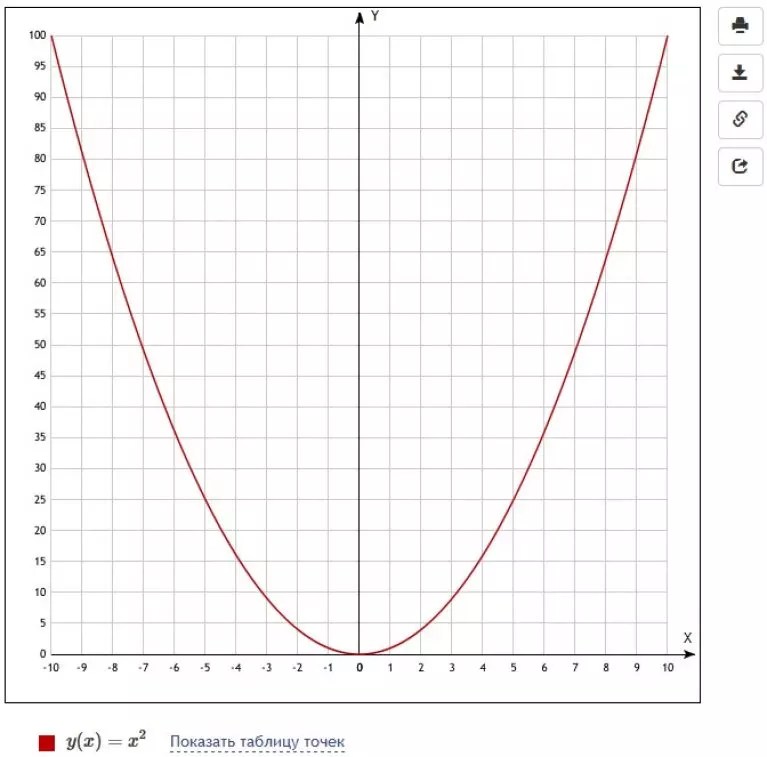 Эта проблема известна как , перекрытие . Такое расположение затрудняет понимание того, где находится масса данных. Распределены ли точки данных равномерно по графику, или существует одна специальная комбинация
Эта проблема известна как , перекрытие . Такое расположение затрудняет понимание того, где находится масса данных. Распределены ли точки данных равномерно по графику, или существует одна специальная комбинация hwy и displ , которая содержит 109 значений?
Вы можете избежать этой сетки, установив регулировку положения на «дрожание». position = "jitter" добавляет небольшое количество случайного шума к каждой точке. Это раздвигает границы, потому что никакие две точки вряд ли получат одинаковое количество случайного шума.
ggplot (данные = миль на галлон) +
geom_point (mapping = aes (x = displ, y = hwy), position = "jitter") Добавление случайности кажется странным способом улучшить ваш график, но, хотя это делает ваш график менее точным в малых масштабах, оно делает ваш график более показательным в больших масштабах. Поскольку это очень полезная операция, в ggplot2 есть сокращение для geom_point (position = "jitter") : geom_jitter () .
Чтобы узнать больше о корректировке положения, просмотрите страницу справки, связанную с каждой корректировкой: ? Position_dodge , ? Position_fill , ? Position_identity , ? Position_jitter и ? Position_stack .
Упражнения
В чем проблема этого участка? Как бы вы могли это улучшить?
ggplot (данные = миль на галлон, отображение = aes (x = cty, y = hwy)) + geom_point ()Какие параметры в
geom_jitter ()управляют величиной дрожания?Сравните и сопоставьте
geom_jitter ()сgeom_count ().Какая настройка положения по умолчанию для
geom_boxplot ()? Создавать Визуализация набора данныхмиль на галлон, который демонстрирует это.
Системы координат
Системы координат, вероятно, самая сложная часть ggplot2. Система координат по умолчанию - это декартова система координат, в которой положения x и y действуют независимо друг от друга для определения местоположения каждой точки. Иногда могут быть полезны и другие системы координат.
Система координат по умолчанию - это декартова система координат, в которой положения x и y действуют независимо друг от друга для определения местоположения каждой точки. Иногда могут быть полезны и другие системы координат.
Coord_flip ()переключает оси x и y. Это полезно (например), если вам нужны горизонтальные коробчатые диаграммы.Это также полезно для длинных ярлыков: это их сложно подогнать без перекрытия по оси абсцисс.ggplot (данные = миль на галлон, отображение = aes (x = класс, y = hwy)) + geom_boxplot () ggplot (данные = миль на галлон, отображение = aes (x = класс, y = hwy)) + geom_boxplot () + Coord_flip ()corre_quickmap ()правильно устанавливает соотношение сторон для карт. Это очень важно, если вы строите пространственные данные с помощью ggplot2 (что, к сожалению, у нас нет места для освещения в этой книге).nz <- map_data ("nz") ggplot (nz, aes (long, lat, group = group)) + geom_polygon (fill = "white", color = "black") ggplot (nz, aes (long, lat, group = group)) + geom_polygon (fill = "white", color = "black") + Coord_quickmap ()corre_polar ()использует полярные координаты. Полярные координаты показывают
интересная связь между гистограммой и диаграммой Кокскомба.
Полярные координаты показывают
интересная связь между гистограммой и диаграммой Кокскомба.бар <- ggplot (data = diamonds) + geom_bar ( отображение = aes (x = вырезать, заполнить = вырезать), Показать.легенда = ЛОЖЬ, ширина = 1 ) + тема (aspect.ratio = 1) + labs (x = NULL, y = NULL) бар + corre_flip () бар + координата_полярная ()
Упражнения
Превратите гистограмму с накоплением в круговую диаграмму с помощью
ordin_polar ().Чем занимается
labs ()? Прочтите документацию.В чем разница между
corre_quickmap ()иcorre_map ()?Что сюжет ниже рассказывает вам об отношениях между городами? и шоссе на милю на галлон? Почему важен
corre_fixed ()? Что значитgeom_abline ()делать?ggplot (данные = миль на галлон, отображение = aes (x = cty, y = hwy)) + geom_point () + geom_abline () + Coord_fixed ()
Многослойная грамматика графики
В предыдущих разделах вы узнали гораздо больше, чем о том, как создавать диаграммы рассеяния, гистограммы и коробчатые диаграммы. Вы узнали фундамент, который можно использовать для построения любого типа графика с помощью ggplot2. Чтобы убедиться в этом, давайте добавим корректировки положения, статистику, системы координат и фасетирование в наш шаблон кода:
Вы узнали фундамент, который можно использовать для построения любого типа графика с помощью ggplot2. Чтобы убедиться в этом, давайте добавим корректировки положения, статистику, системы координат и фасетирование в наш шаблон кода:
ggplot (data = ) +
(
отображение = aes (<КАРТЫ>),
stat = ,
position = <ПОЛОЖЕНИЕ>
) +
+
Наш новый шаблон принимает семь параметров, слова в квадратных скобках, которые появляются в шаблоне.На практике вам редко нужно указывать все семь параметров для построения графика, потому что ggplot2 предоставит полезные значения по умолчанию для всего, кроме данных, сопоставлений и функции geom.
Семь параметров в шаблоне составляют грамматику графики, формальную систему построения графиков. Грамматика графики основана на понимании того, что вы можете однозначно описать любой график как комбинацию набора данных, геометрии, набора сопоставлений, статистики, корректировки положения, системы координат и схемы фасетирования.
Чтобы увидеть, как это работает, подумайте, как вы можете построить базовый график с нуля: вы можете начать с набора данных, а затем преобразовать его в информацию, которую вы хотите отобразить (со статистикой).
Затем вы можете выбрать геометрический объект для представления каждого наблюдения в преобразованных данных. Затем вы можете использовать эстетические свойства геометрии для представления переменных в данных. Вы бы сопоставили значения каждой переменной с уровнями эстетики.
Затем вы должны выбрать систему координат для размещения геометрии.Вы должны использовать расположение объектов (которое само по себе является эстетическим свойством) для отображения значений переменных x и y. В этот момент у вас будет полный график, но вы можете дополнительно настроить положения геометрии в системе координат (корректировка положения) или разбить график на подзаголовки (фасетирование). Вы также можете расширить график, добавив один или несколько дополнительных слоев, где каждый дополнительный слой использует набор данных, геометрию, набор сопоставлений, статистику и корректировку положения.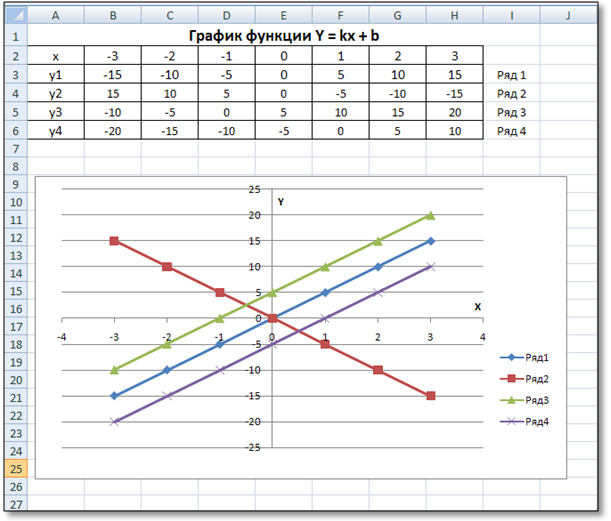
Вы можете использовать этот метод для построения любого участка , который вы себе представляете. Другими словами, вы можете использовать шаблон кода, который вы изучили в этой главе, для построения сотен тысяч уникальных графиков.
Как создать динамический диапазон диаграммы в Excel
Когда вы создаете диаграмму в Excel и исходные данные меняются, вам необходимо обновить источник данных диаграммы, чтобы убедиться, что он отражает новые данные.
Если вы работаете с часто обновляемыми диаграммами, лучше создать динамический диапазон диаграмм.
Что такое динамический диапазон диаграммы?
Динамический диапазон диаграммы - это диапазон данных, который обновляется автоматически при изменении источника данных.
Этот динамический диапазон затем используется в качестве исходных данных на диаграмме. По мере изменения данных динамический диапазон обновляется мгновенно, что приводит к обновлению диаграммы.
Ниже приведен пример диаграммы, в которой используется динамический диапазон диаграммы.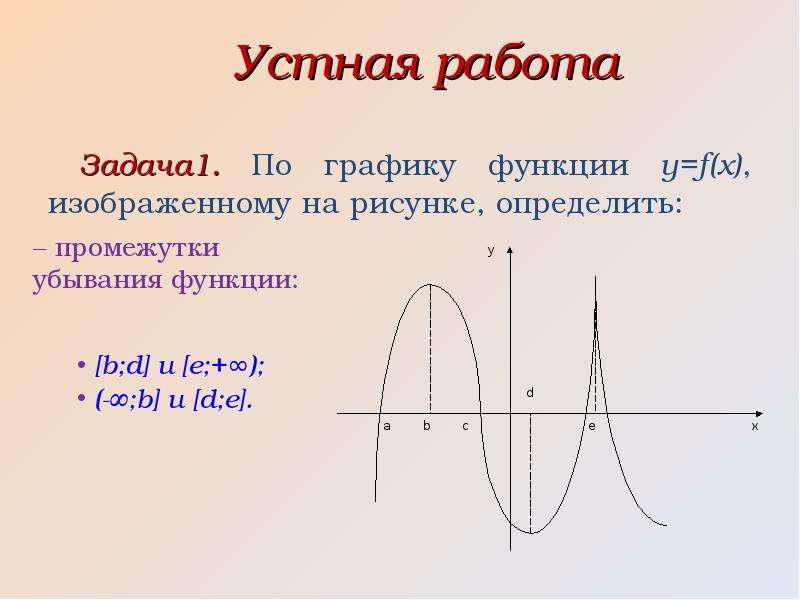
Обратите внимание, что диаграмма обновляется с новыми точками данных за май и июнь, как только данные будут введены.
Как создать динамический диапазон диаграммы в Excel?
Существует два способа создания диапазона динамической диаграммы в Excel:
- Использование таблицы Excel
- Использование формул
В большинстве случаев использование таблицы Excel является лучшим способом создания динамических диапазонов в Excel.
Давайте посмотрим, как работает каждый из этих методов.
Щелкните здесь, чтобы загрузить файл примера .
Использование таблицы Excel
Использование таблицы Excel - лучший способ создания динамических диапазонов, поскольку они автоматически обновляются при добавлении к ним новой точки данных.
Таблица Excel была представлена в версии Windows для Excel 2007, и если у вас есть более ранние версии, вы не сможете ее использовать (см. Следующий раздел о создании диапазона динамических диаграмм с помощью формул).
Pro Совет: Чтобы преобразовать диапазон ячеек в таблицу Excel, выберите ячейки и используйте сочетание клавиш - Control + T (удерживая клавишу Control, нажмите клавишу T). В приведенном ниже примере вы можете видеть, что как только я добавляю новые данные, таблица Excel расширяется, чтобы включить эти данные как часть таблицы (обратите внимание, что рамка и форматирование расширяются, чтобы включить их в таблицу).
Теперь нам нужно использовать эту таблицу Excel при создании диаграмм.
Вот точные шаги для создания динамической линейной диаграммы с использованием таблицы Excel:
- Выберите всю таблицу Excel.
- Перейдите на вкладку Вставка.
- В группе диаграмм выберите диаграмму «Линия с маркерами».
Вот и все!
Приведенные выше шаги позволят вставить линейную диаграмму, которая будет автоматически обновляться при добавлении дополнительных данных в таблицу Excel.
Обратите внимание, что хотя добавление новых данных автоматически обновляет диаграмму, удаление данных не приведет к полному удалению точек данных. Например, если вы удалите 2 точки данных, на диаграмме отобразится некоторое пустое пространство справа. Чтобы исправить это, перетащите синюю отметку в правом нижнем углу таблицы Excel, чтобы удалить удаленные точки данных из таблицы (как показано ниже).
Хотя я взял в качестве примера линейную диаграмму, вы также можете создавать другие типы диаграмм, такие как столбчатые / гистограммы, используя эту технику.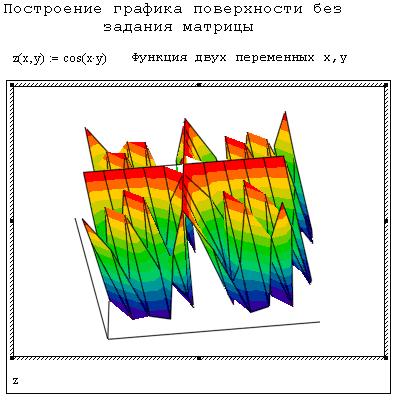
Использование формул Excel
Как я уже упоминал, использование таблицы Excel - лучший способ создать диапазоны динамических диаграмм.
Однако, если по какой-то причине вы не можете использовать таблицу Excel (возможно, если вы используете Excel 2003), существует другой (немного сложный) способ создания диапазонов динамических диаграмм с использованием формул Excel и именованных диапазонов.
Предположим, у вас есть набор данных, как показано ниже:
Чтобы создать динамический диапазон диаграммы из этих данных, нам необходимо:
- Создать два динамических именованных диапазона, используя формулу СМЕЩЕНИЕ (по одному для каждого параметра «Значения» и Столбец «Месяцы»).Добавление / удаление точки данных автоматически обновит эти именованные диапазоны.
- Вставьте диаграмму, которая использует именованные диапазоны в качестве источника данных.
Теперь позвольте мне подробно объяснить каждый шаг.
Шаг 1.
 Создание динамических именованных диапазонов
Создание динамических именованных диапазоновНиже приведены шаги по созданию динамических именованных диапазонов:
- Перейдите на вкладку «Формулы».
- Щелкните «Диспетчер имен».
- В диалоговом окне «Диспетчер имен» укажите имя как ChartValues и введите следующую формулу в поле «Относится к части»: = OFFSET (Formula! $ B $ 2 ,,, COUNTIF (Formula! $ B $ 2: $ B $ 100, ” <> ”))
- Щелкните OK.
- В диалоговом окне «Диспетчер имен» нажмите «Создать».
- В диалоговом окне «Диспетчер имен» укажите имя как ChartMonths и введите следующую формулу в поле «Относится к части»: = OFFSET (Formula! $ A $ 2 ,,, COUNTIF (Formula! $ A $ 2: $ A $ 100, » <> ”))
- Нажмите ОК.
- Нажмите «Закрыть».
Вышеупомянутые шаги создали два именованных диапазона в Рабочей книге - ChartValue и ChartMonth (они относятся к диапазонам значений и месяцев в наборе данных соответственно).
Если вы обновите столбец значений, добавив еще одну точку данных, именованный диапазон ChartValue теперь автоматически обновится, чтобы отобразить в нем дополнительную точку данных.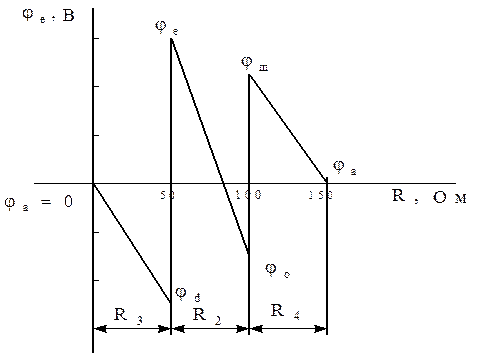
Здесь волшебство творится с помощью функции СМЕЩЕНИЕ.
В формуле именованного диапазона ChartValue мы указали B2 в качестве контрольной точки. Формула СМЕЩЕНИЕ начинается там и распространяется на все заполненные ячейки в столбце.
Та же логика работает и в формуле именованного диапазона ChartMonth.
Шаг 2. Создание диаграммы с использованием этих именованных диапазонов
Теперь все, что вам нужно сделать, это вставить диаграмму, которая будет использовать именованные диапазоны в качестве источника данных.
Вот шаги, чтобы вставить диаграмму и использовать динамические диапазоны диаграммы:
Вот и все! Теперь ваша диаграмма использует динамический диапазон и будет обновляться при добавлении / удалении точек данных в диаграмме.
Несколько важных вещей, которые следует знать при использовании именованных диапазонов с диаграммами:
- В данных диаграммы не должно быть пустых ячеек.Если есть пробел, именованный диапазон не будет относиться к правильному набору данных (так как общее количество приведет к тому, что он будет относиться к меньшему количеству ячеек).
- При использовании имени листа в источнике диаграммы необходимо соблюдать соглашение об именах. Например, если имя листа представляет собой одно слово, такое как Формула, вы можете использовать = Формула! ChartValue. Но если есть более одного слова, например Formula Chart, вам нужно использовать = ’Formula Chart’! ChartValue.
Вам также могут понравиться следующие руководства по Excel:
Векторный 3D-плоттер | Academo.org
Интерактивный сюжет из 3D векторов. Посмотрите, как два вектора связаны с их результирующим, разностным и перекрестным произведением.
Математика Геометрия График участок вектор
Приведенная выше демонстрация позволяет вам ввести до трех векторов в форме (x, y, z). Нажатие кнопки рисования отобразит векторы на диаграмме (масштаб диаграммы будет автоматически настроен, чтобы соответствовать величине векторов). Вы можете перетащить диаграмму и увеличить или уменьшить масштаб с помощью прокрутки с помощью мыши.При нажатии на конец вектора также отображаются его отдельные компоненты.
В демонстрации также есть возможность построить 3 других вектора, которые можно вычислить из первых двух входных векторов. Первый из них является результирующим, и он получается, когда компоненты каждого вектора складываются. Если результат \ (\ textbf {c} \), то
\ [\ textbf {c} = \ textbf {a} + \ textbf {b} \] \ [\ left (\ begin {array} {c} c_x \\ c_y \\ c_z \ end {array} \ right) = \оставили( \ begin {array} {c} а_х \\ а_у \\ a_z \ end {array} \ right) + \оставили( \ begin {array} {c} b_x \\ к \\ b_z \ end {массив} \верно) знак равно \оставили( \ begin {array} {c} a_x + b_x \\ а_у + Ь_у \\ a_z + b_z \ end {массив} \верно) \]Аналогичным образом, разница в том, что вы получаете, когда вычитаете один вектор из другого, в данном случае \ (\ textbf {d} \),
\ [\ textbf {d} = \ textbf {a} - \ textbf {b} \] \ [\ left (\ begin {array} {c} d_x \\ d_y \\ d_z \ end {array} \ right) = \оставили( \ begin {array} {c} а_х \\ а_у \\ a_z \ end {array} \ right) - \оставили( \ begin {array} {c} b_x \\ к \\ b_z \ end {массив} \верно) знак равно \оставили( \ begin {array} {c} a_x - b_x \\ а_у - б_у \\ a_z - b_z \ end {массив} \верно) \]Наконец, векторное произведение (также известное как перекрестное произведение) определяется как
\ [\ textbf {e} = \ textbf {a} \ times \ textbf {b} = \ lvert a \ rvert \ \ lvert b \ rvert \ \ sin (\ theta) \ hat {n} \] \ [\ left (\ begin {array} {c} бывший \\ e_y \\ e_z \ end {array} \ right) = \оставили( \ begin {array} {c} а_х \\ а_у \\ a_z \ end {array} \ right) \ раз \оставили( \ begin {array} {c} b_x \\ к \\ b_z \ end {массив} \верно) знак равно \оставили( \ begin {array} {c} a_yb_z - a_zb_y \\ a_zb_x - a_xb_z \\ a_xb_y - a_yb_x \ end {массив} \верно) \]С геометрической точки зрения длина векторного произведения равна произведению величин \ (\ textbf {a} \) и \ (\ textbf {b} \), умноженных на синус угла между ними.Он указывает в направлении \ (\ hat {n} \), который является вектором, указывающим прямо из плоскости, в которой лежат \ (\ textbf {a} \) и \ (\ textbf {b} \). Это означает, что если два вектора указывают в одном (или точно противоположном) направлении, то их перекрестное произведение будет равно нулю. Попробуйте это выше!
Кредиты
- Спасибо пользователю https://github.com/harshaxnim за создание возможности добавлять дополнительные векторы, а также за реализацию других улучшений в коде этой демонстрации
Постройте модель солнечной системы
Я только дал вам размеры и расстояния до планет. Если вы хотите увидеть и спутники планет, нажмите здесь, чтобы перейти на гораздо более обширную страницу (а также на более длительное время загрузки!)
Одним из самых захватывающих упражнений, которые я когда-либо делал в детстве, было создание масштабной модели Солнечной системы. На большинстве картинок в моих книгах расстояние между планетами кажется небольшим, и по ним легко путешествовать. Музеи тоже не помогли.Модели, которые они показывали, обычно имели размеры планет в масштабе, но расстояния между ними были совершенно другого масштаба, создавая впечатление довольно сплоченной семьи.
Я сделал свою первую масштабную модель на рулоне бумажной ленты для телетайпа (кто-нибудь помнит этот материал?). На этой 1-дюймовой ленте мое Солнце имело размер ленты - 1 дюйм в диаметре. Все началось хорошо. Меркурий находился всего в 3-1 / 2 футах от Солнца, а Земля - почти в 9 футах от Солнца. На что я не рассчитывал, так это на то, что Плутон находится на высоте 354 фута по ленте! Я израсходовал почти весь рулон.
Я также рассчитал размеры, которые я должен сделать для точек, представляющих планеты. Я обнаружил, что даже самая большая планета, Юпитер, должна иметь размер пятна меньше 1/8 дюйма. Другие планеты, особенно маленькие каменистые внутренние планеты, будут фактически невидимыми пятнами пыли.
Излишне говорить, что это был потрясающий опыт. Это одно упражнение научило меня истинному значению слова «пространство». Это определенно заставило меня почувствовать себя незначительным, глядя на масштаб Солнечной системы - не говоря уже об остальной Вселенной!
Теперь у нас есть отличные инструменты, такие как электронные таблицы, для выполнения численных расчетов за нас.Ниже вы можете скачать файлы формата OpenOffice (или Libre Office), Apple Numbers или Excel. В этих таблицах вы устанавливаете масштаб модели, вводя радиус Солнца. Затем листы должны рассчитать все остальное на основе этого числа.
Скачать электронную таблицу в формате Apple NumbersСкачать электронную таблицу в формате Excel
Скачать электронную таблицу в формате OpenOffice
Ссылки на другие ресурсы Солнечной системы
Спасибо Биллу Арнетту за его фантастический веб-сайт «Девять планет».
© 1997; Рон Хипшман, Exploratorium
Координатная плоскость в режиме онлайн - заполнение онлайн, возможность печати, заполняемое, пустое
Комментарии и помощь по координатной миллиметровой бумаге онлайн
Видеоинструкция и помощь по заполнению координатной плоскости онлайн
Инструкции и справка по форме координатной плоскости
Привет, я Роб, добро пожаловать в математические шалости. В этом уроке мы собирались узнать кое-что, что является важной основой для множества математических задач, включая те, с которыми вы столкнетесь при изучении базовой алгебры. Мы собирались узнать о построении графиков, что в основном означает использование математических соотношений и превращение их в картинки. Привет, друзья, добро пожаловать. назад к «Радость построения графиков» Мы собираемся продолжить с того места, где остановились. У нас уже есть эта прекрасная красивая функция прямо здесь. Но ей нужен друг. И мы собирались сделать это, добавив несколько точек. Итак, давайте поместим следующую точку прямо здесь. Теперь все, что нам нужно. нужно соединить эти точки, потому что они все друзья И что делать друзьям Они остаются на связи О, и посмотрите на это Это красиво Ну не та картинка, которую вы бы повесили на стену Создание графиков просто означает визуальное представление уравнения или набора данных, так что вы можете лучше понять это. Это способ помочь вам буквально УВИДЕТЬ, как работает математика. Когда математика - это просто набор чисел и символов на странице, это может быть довольно абстрактно и сложно связать с ним Но построение графиков похоже на окно в абстрактный мир математики, которое помогает нам увидеть его более ясно. На самом деле фокус нашего сегодняшнего урока на самом деле немного похож на окно, которое называется Координатная плоскость Координатная плоскость это платформа или этап, на котором будет происходить построение графика. Но чтобы понять, как это работает, нам сначала нужно начать с его ближайшего родственника; Числовая линия Вы помните, как работает числовая линия справа Числовая линия начинается с нуля и представляет положительные числа, когда вы двигаетесь вправо, и отрицательные числа, когда вы перемещаетесь влево И обычно есть отметки, показывающие, где находится каждое целое число. клонирование этой числовой линии и поворот копии против часовой стрелки на 90 градусов так, чтобы вторая числовая линия была перпендикулярна первой и пересекалась в своих нулевых точках. Теперь у нас есть числовая плоскость. числовая линия, но это второе измерение делает ее намного более полезной С помощью простой 1-мерной числовой линии мы могли бы показать, где были расположены различные числа вдоль этой линии, путем рисования или нанесения точек. Но независимо от того, сколько точек мы наносим, они всегда находятся на одной линии. с помощью двумерной числовой плоскости мы можем наносить точки в любом месте этой двумерной области, и это открывает целый новый мир возможностей. С помощью 1-мерной числовой линии построение точек было легким. просто нужно было одно число, чтобы сказать вам, где построить точку. Но с двумерной числовой плоскостью вам действительно нужны ДВА числа для построения каждой точки. Эти два числа называются координатами, потому что они имеют один и тот же ранг или порядок, и они работают вместе, чтобы указать местоположения точки на числовой плоскости На самом деле, именно поэтому числовую плоскость часто называют координатной плоскостью. Это этап для построения координат.

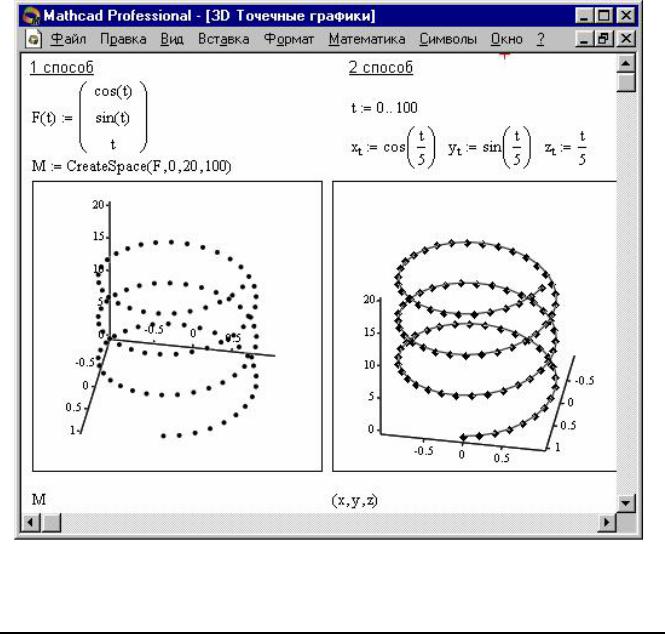 dat с настройками по умолчанию.
dat с настройками по умолчанию.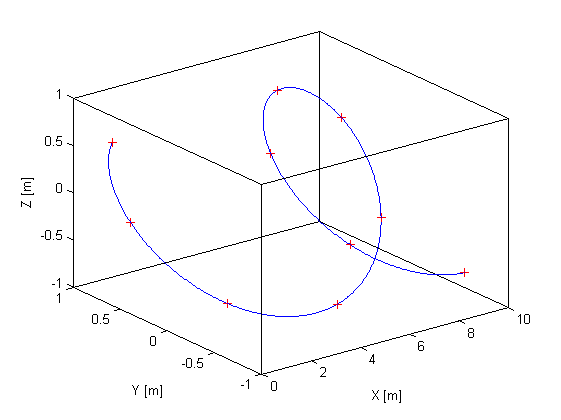

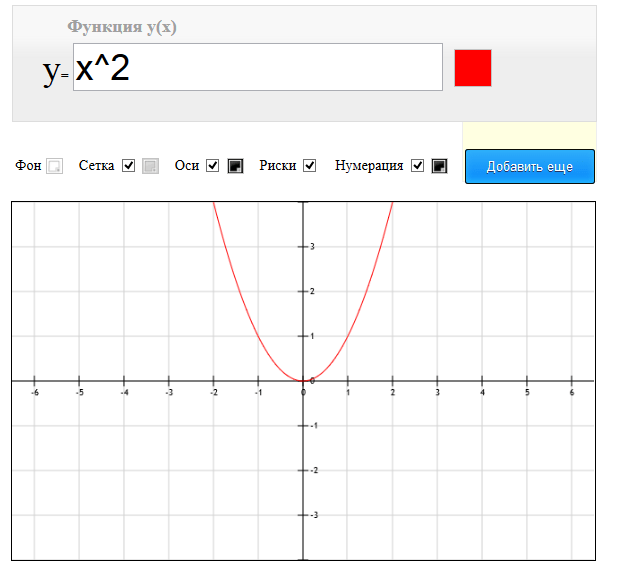
 В нашем случае это диапазон C1: D13. Не выбирайте другие столбцы, чтобы не запутать Excel.
В нашем случае это диапазон C1: D13. Не выбирайте другие столбцы, чтобы не запутать Excel.

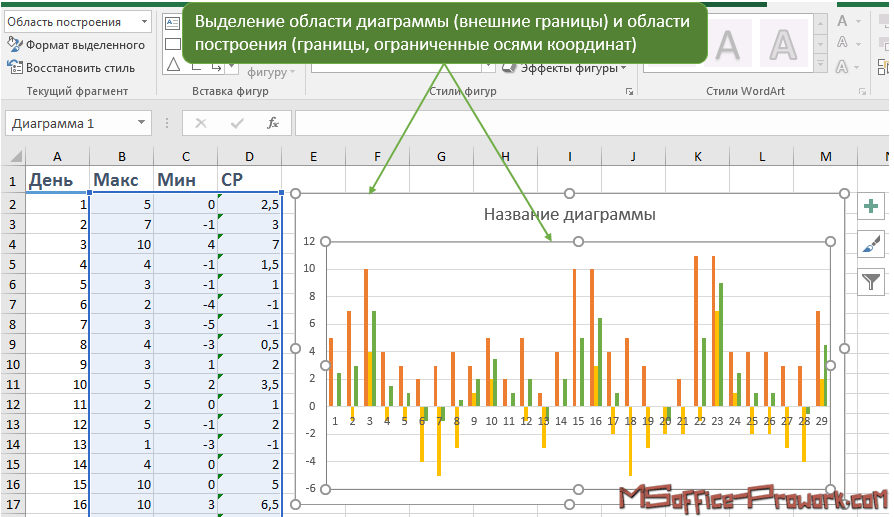 Автомобиль с низкой топливной экономичностью потребляет больше топлива, чем автомобиль с высокой топливной экономичностью.
топливная экономичность, когда они едут на одинаковое расстояние.
Автомобиль с низкой топливной экономичностью потребляет больше топлива, чем автомобиль с высокой топливной экономичностью.
топливная экономичность, когда они едут на одинаковое расстояние.

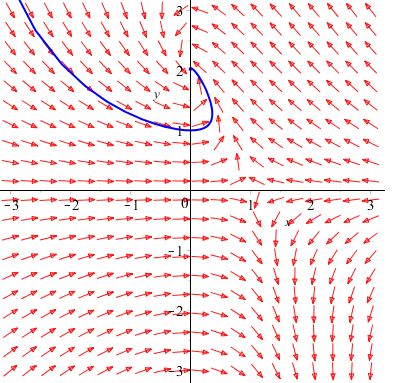 ~ cyl)
~ cyl)  legend = FALSE
legend = FALSE 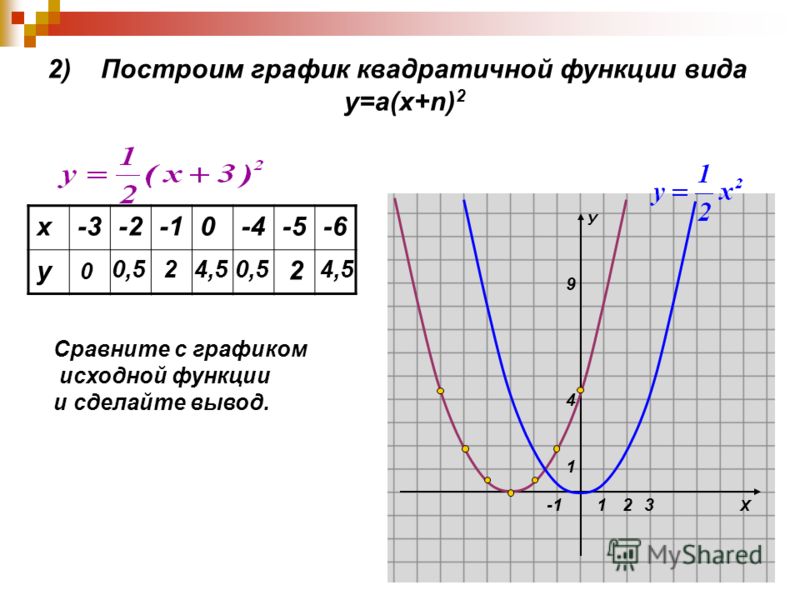
 К сожалению, когда люди небрежно говорят о гистограммах, они могут
относится к этому типу столбчатой диаграммы, где высота столбца уже равна
присутствует в данных, или на предыдущей гистограмме, где высота столбца
генерируется путем подсчета строк.
К сожалению, когда люди небрежно говорят о гистограммах, они могут
относится к этому типу столбчатой диаграммы, где высота столбца уже равна
присутствует в данных, или на предыдущей гистограмме, где высота столбца
генерируется путем подсчета строк. под названием «вычисляемые переменные».
под названием «вычисляемые переменные». Прочтите документацию и составьте список всех
пары. Что у них общего?
Прочтите документацию и составьте список всех
пары. Что у них общего?
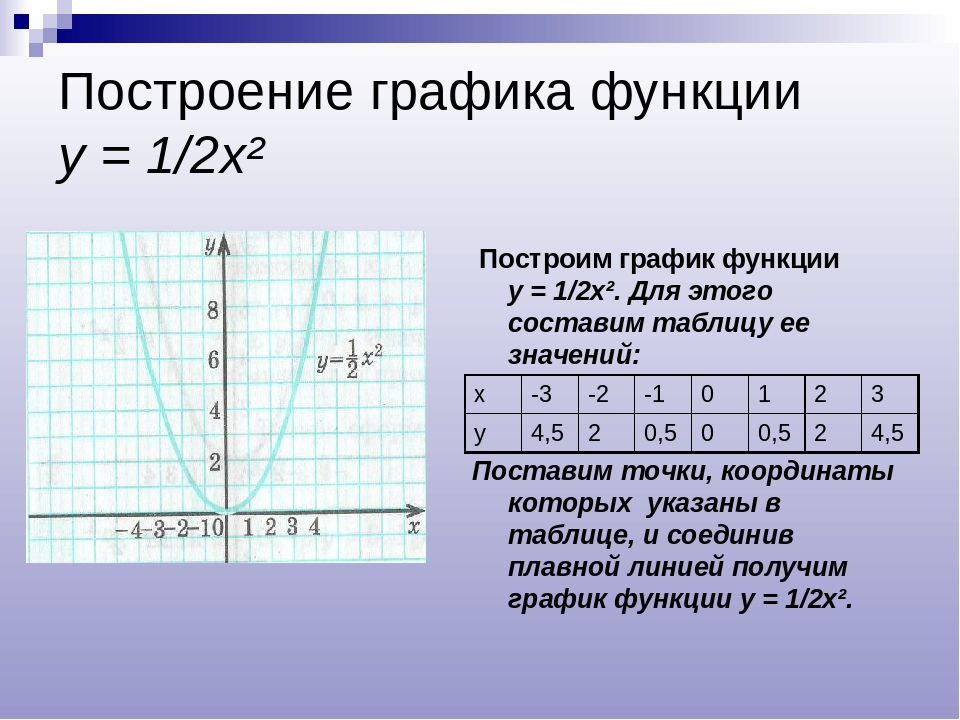 Полярные координаты показывают
интересная связь между гистограммой и диаграммой Кокскомба.
Полярные координаты показывают
интересная связь между гистограммой и диаграммой Кокскомба.