Mathway | Решение алгебраических задач
Mathway | Решение алгебраических задачNew Messages
User is Typing
Этот веб-сайт использует cookie файлы, чтобы сделать использование нашего ресурса максимально удобным для вас.
- число
- буква
- специальный символ: @$#!%*?&

На своем жизненном пути каждому приходилось или придется встретиться с такой прекрасной и точной наукой как Математика. Она развивает логическое и абстрактное мышление, улучшает способность быстро соображать и принимать решения. На основе именно этой науки строится описание нашего мира.
С чего начинается математика?
Базовой составляющей математики является раздел Арифметика – операции подсчета, измерения и описания форм объектов. Это базис, на который опираются знания о структуре, порядке и отношениях. Именно они составляют суть науки. Школьная программа начинается с Арифметики, которую и предстоит освоить каждому ребенку, переступившему порог школы.
Поняв принцип математических операций, необходимо научиться быстро и безошибочно решать любые примеры по математике. И тут все упирается в терпение и регулярную практику, в следствие которой подсчитывать ответ становится все легче и легче.
Виды примеров по математике:
- С натуральными числами
- С дробными числами
- С отрицательными числами
- С иррациональными числами
- С тригонометрическими выражениями
Так же в математических примерах можно встретить комплексные числа. Роль каждых из чисел очень велика при решении и описании разных проблем с помощью математики. В дальнейшем в разделе Алгебра вместо чисел будут использоваться разнообразные выражения, но суть останется прежняя.
С чего начать тренировку в решении примеров по математике ?
Конечно, начинать надо с самого простого и банального, с того что является самой основой. Обычные примеры начальной школы с натуральными числами. На их изучение и практику в школе уделяют большое количество времени, и дети на протяжении нескольких месяцев или лет, занимаются решением примеров, списывая задание с доски, открывая учебник или рабочую тетрадь, где один за одним решают примеры.
Предлагаем вам упрощенный способ развития навыков решения.
 |
Онлайн тренажер устного счета192 разнообразных режима тренировок: Уравнения, сравнения, отрицательные числа |
С помощью специального онлайн «Тренажера устного счета», где можно быстро и легко практиковаться в решении простых арифметических примеров.
Приложение позволяет быстро анализировать и исправлять допущенные ошибки, помогает с ответом при наличии сложного примера, а также ведет полную статистику выполненной работы. Родителям не придется тратить свое время на поиск математических примеров для тренировки ребенка, а потом долго и скрупулезно проверять их вручную.
В свою очередь дети сосредотачиваются на решении примера и не тратят время на поиск его среди массы похожих примеров на страницах учебников, не отвлекаются на переписывание его из учебника в тетрадь, проверяя по десять раз верность переписанного. Все это существенно ускоряет процесс обучения, уделяя внимание именно самому главному – решению самих примеров по математике!
Зачем нужен навык решения примеров по математике?
Несомненно, не всем в жизни нужно быть живым компьютером с развитым навыком устного счета. Однако очень часто происходят ситуации, когда этот навык выручает. Ведь в современном мире, где всё вокруг строится на основе математических законов, иметь такой приятный для себя бонус как хорошее умение быстро что-либо просчитывать очень круто! Никогда не знаешь на перед что и когда тебе понадобится, так почему бы не уделить немного времени этому сейчас, чтобы по жизни не попадать в неловкие ситуации, к тому же научиться этому делу довольно легко!
Очень многие ошибочно полагают, что стоит начинать учиться только тогда, когда они столкнуться с этими проблемами и это будет необходимым по жизни. Однако наш совет: освоить базовые навыки решения математических примеров и устного счета стоит как можно раньше, пока ум молод, свеж и гибок в плане обучения, а человек не занят взрослыми надоедливыми делами.
Научно доказано, если регулярно решать арифметические примеры, то:
- Сохраняется ясность ума
- Развивается логическое мышление
- Улучшается мозговая активность
- Повышается внимательность и концентрация
- Проявляется терпение и трудолюбие
- Развивается креативность
Как развить навык решения примеров по математике?
Надо понимать, что навык решения напрямую связан и количеством решаемых примеров. Чем больше примеров Вы прорешиваете, тем лучше начинает работать и справляться с ними мозг. Конечно же, это не означает, что надо убить все свое время только на решение примеров по математике. Очень важное значение тут имеет регулярность!
Каждый день практикуясь в небольшое выделенное для себя время, можно быстро развить свой навык устного счета до приличных возможностей. Необходимо также уделять внимание разнообразию примеров (их видам) – то есть постепенно решать все более сложные и интересные примеры, не останавливаясь на простых!
Также о навыках решения примеров по математике можно прочитать в статье «Как научиться считать в уме».
Как заставить себя решать примеры по математике?
Зачастую очень тяжело заставить себя заниматься делом, всё больше хочется отдохнуть, не утруждать себя надоедливым занятием, даже осознавая, что это нужно и необходимо. Немногие дети стремятся самостоятельно поучаствовать в своем развитии или хотя бы выполнить домашнее задание.
Поэтому в приложение «Тренажер устного счета» был добавлен игровой соревновательный момент. Возможно это изменит подход к скучному обучению, сделав этот процесс более интересным и завлекающим. Предлагаем самостоятельно опробовать данное приложение и оценить его.
Желаем успехов в решении!
Решение задач по мат. анализу
Mathway | Решение задач по мат. анализуUser is Typing
Этот веб-сайт использует cookie файлы, чтобы сделать использование нашего ресурса максимально удобным для вас.
Убедитесь, что ваш пароль содержит не менее 8 символов и как минимум один из следующих символов:
- число
- буква
- специальный символ: @$#!%*?&
photomatch онлайн решать
Вы искали photomatch онлайн решать? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и алгебра решение по фото, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «photomatch онлайн решать».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как photomatch онлайн решать,алгебра решение по фото,задачи решение по фото,калькулятор онлайн по фото,калькулятор онлайн фото,калькулятор по фото,калькулятор по фото онлайн,калькулятор по фотографии онлайн,калькулятор с камерой онлайн,калькулятор фото матч онлайн,калькулятор фото онлайн,математика по фото решение,математика решение по фото,математика решение по фото онлайн,математика фото решение,онлайн калькулятор по фото,онлайн калькулятор по фотографии,онлайн калькулятор с камерой,онлайн решение задач по фото,онлайн решение по картинке,онлайн решение по фото,онлайн решение примеров по фото,онлайн фото калькулятор,по фото решить пример,по фото решить уравнение,приложение для решение примеров по алгебре,приложение для решения примеров,приложение для решения примеров по алгебре,приложение для решения примеров по математике,приложения для решения примеров,решение задач онлайн по фото,решение задач онлайн по фотографии,решение задач по фото,решение задач по фото онлайн,решение задач по фотографии онлайн,решение задач фото,решение задачи по фото,решение математики по фото,решение онлайн по картинке онлайн,решение онлайн по фото,решение онлайн по фото математика,решение по картинке онлайн,решение по математике по фото,решение по фото алгебра,решение по фото математика,решение по фото математика онлайн,решение по фото онлайн,решение по фото онлайн математика,решение по фотографии онлайн,решение по фотографии онлайн алгебра,решение примера по фото,решение примеров онлайн по фото,решение примеров по фото,решение примеров по фото онлайн,решение примеров по фото онлайн бесплатно,решение примеров по фотографии,решение примеров фото,решение уравнений онлайн по фото,решение уравнений по фото,решение уравнений по фото онлайн,решение уравнений фото,решение фото задач,решение фото математика,решить задачу по фото,решить по фото задачу,решить пример онлайн по фото,решить пример по фото,решить пример по фото онлайн,решить уравнение онлайн по фото,решить уравнение по фото,решить уравнение по фото онлайн,сфоткать задание и решить,фантомас онлайн калькулятор,фото калькулятор онлайн,фото калькулятор онлайн без скачивания,фото математика онлайн,фото математика решение,фото матч калькулятор онлайн,фото решение задач,фото решение математика,фото решение онлайн,фото решение примеров,фото решение уравнений. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и photomatch онлайн решать. Просто введите задачу в окошко и нажмите «решить» здесь (например, задачи решение по фото).
Где можно решить любую задачу по математике, а так же photomatch онлайн решать Онлайн?
Решить задачу photomatch онлайн решать вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
найти область определения функции онлайн | калькулятор предназначен для определения четности и нечетности функции |
определения точек пересечения графика функции с осями координат | нахождение асимптот графика функции онлайн |
методом неопределенных коэффициентов | онлайн калькулятор для определения периодичности |
и интервалы его выпуклости и вогнутости онлайн | кусочно-непрерывных функций |
u=f(x,y,z) | и построение графика |
найти интервалы знакопостоянства | они же точки пересечения |
и интервалы монотонности | обратное преобразования Лапласа онлайн |
интегральное преобразование Лапласа онлайн | по формуле общего члена ряда |
вычислить угол наклона | рассчитать угловой коэффициент |
онлайн калькулятор | достаточно задать функцию, чтобы получить значения максимума |
одно из необходимых условий наличия минимума | функция в этих точках не является непрерывной |
провести исследование графика функции | решать пределы любых функций онлайн |
составить и решить уравнение касательно | найти как косинусы и синусы угла, так и решить выражения |
функции относятся к простейшим | график функции |
раскладывается в степенной ряд по степеням | любое число раз и в некоторой окрестности |
абсолютно любую четную функцию можно разложить в ряды Фурье | нахождение формулы |
найти прямую перпендикулярной прямой | в полярных координатах на плоскости |
найти прямую перпендикулярной прямой | в полярных координатах на плоскости |
в полярных координатах | построить полином по точкам |
переменной | на отрезке в заданном интервале |
на отрезке в заданном интервале | найти точки экстремума функции |
найти область значений фукции | найти нули производной |
значение функции на отрезке | производная функции равна 0 или не существует |
| Найти угловые точки графика функции |
Калькулятор вычисления суммы, разности, произведения и частного столбиком отобразит все этапы решения примера и даст продробное решение. Калькулятор может сложить, вычесть, умножить и разделить столбиком десятичные дроби и целые числа. Для записи десятичной дроби используйте точку либо запятую (например, 1.12 или 1,12).
Как складывать столбиком
Для того, чтобы сложит два числа столбиком, необходимо записать большее число над меньшим и выполнить последовательное сложение справа на лево, например, сложим столбиком 345 и 67.
345 + 67 = 412
110
+345
67
412
1) 5 + 7 = 12; 2 пишем, число 1 запишем над числом 4.
2) 4 + 6 = 10; 10 + 1 = 11; 1 пишем, 1 запишем над числом 3.
3) Под числом 3 нет слагаемого, поэтому просто прибавим 3 + 1 = 4
Получилось 412
Приведем еще один пример: 1567 + 761
1567 + 761 = 2328
1100
+1567
761
2328
1) 7 + 1 = 8, запишем 8.
2) 6 + 6 = 12; 2 пишем, 1 запишем над числом 5.
3) 5 + 7 = 12; 12 + 1 = 13; 3 пишем, 1 запишем над числом 1.
4) Под числом 1 нет слагаемого, поэтому просто прибавим 1 + 1 = 2
Как складывать столбиком десятичные дроби
Для того, чтобы сложить две десятичные дроби, необходимо записать одну десятичную дробь над другой, совместив их точки. Приведем пример: 123.345 + 46.02
123.345 + 46.02 = 169.365
+123.345
46.020
169.365
1) Запишем число 123.345 над числом 46.02
2) Под числом 5 нет слагаемого, поэтому просто запишем его внизу.
2) Далее сложим 2 и 4; 2 + 4 = 6; запишем 6 внизу.
3) 3 + 0 = 3; записываем 3.
4) Ставим точку
5) 3 + 6 = 9; записываем 9 внизу.
6) 2 + 4 = 6; записываем 6 внизу.
7) Так как под числом 1 нет слагаемого, просто сносим его вниз. Запишем число 1 внизу.
Итак, у нас получилось 169.365
Приведем следующий пример: 123.99 + 12.99
123.99 + 12.99 = 136.98
001010
+123.99
12.99
136.98
1) 9 + 9 = 18; 8 пишем, 1 запишем над числом 9.
2) 9 + 9 = 18; 18 + 1 = 19; 9 пишем, 1 запишем над числом 3.
3) Ставим точку.
4) 2 + 3 = 5; 5 + 1 = 6; 6 запишем внизу
5) 2 + 1 = 3; 3 запишем внизу.
6) Так как под числом 1 нет слагаемого, просто сносим его вниз. Запишем число 1 внизу.
Ответ: 136.98
Для того чтобы сложить десятичную дробь с целым числом, необходимо сложить целую часть десятичной дроби с целым числом. Сложим, например, 23 и 0.34. У числа 23, после точки поставим столько нолей, сколько чисел после точки у десятичной дроби.
23 + 0.34 = 23.34
+23.00
0.34
23.34
1) 0 + 4 = 4. Запишем 4.
2) 0 + 3 = 3. Запишем 3.
3) Ставим точку
4) 3 + 0 = 3. Запишем 3
5) Под числом 2 нет слагаемого, поэтому просто сносим его вниз.
Ответ: 23.34
Как вычитать столбиком
Для того, чтобы вычесть два числа столбиком, необходимо записать большее число над меньшим и выполнить последовательное вычитание, например, вычтем столбиком 456 и 89.
456 — 89 = 367
..0
—456
89
367
1) Из 6-ти вычесть число 9 не получится, так как 6 меньше девяти, поэтому займем 1 у числа 5 и поставим над ним точку, получим вместо числа 6 число 16. Отнимем от 16 число 9; 16 – 9 = 7; запишем 7.
2) Так как мы заняли число 1 у числа 5, то теперь осталось число 4. Из числа 4 вычесть число 8 не получится, поэтому займем 1 у соседнего числа 4 и поставим над ним точку, получим вместо числа 4 число 14. Отнимем от числа 14 число 8 = 6. Запишем 6.
3) Под числом 4 нет вычитаемого, поэтому отнимем от числа 4 число 1 (так как мы занимали 1-цу): 4 -1 = 3; запишем число 3.
Получилось 367.
Приведем еще один пример: 307 – 58
307 — 58 = 249
..0
—307
58
249
1) Из числа 7 вычесть число 8 не получится, так как 7 меньше 8, поэтому займем 1 у ноля. Поставим над нолем точку. Когда мы занимаем 1-цу у нуля, ноль становится числом 9! получим вместо 0 число 9. Однако у ноля не получится взять единицу, поэтому двигаемся влево и занимаем единицу у числа 3 и ставим над ним точку; отнимем от 17 число 8; 17 – 8 = 9; запишем 9.
2) Так как мы заняли число 1 у ноля, то теперь осталось число 9. Отнимем от числа 9 число 5 = 4. Запишем 4.
3) Под числом 3 нет вычитаемого, но мы помним, что мы заняли единицу у числа 3, поэтому 3-1 = 2. Запишем число 2.
Получилось 249.
Как вычитать столбиком десятичные дроби
Для того, чтобы отнять из десятичной дроби целое число, либо из целого числа вычесть десятичную дробь нужно у целого числа после точки записать столько нолей, сколько чисел после точки у десятичной дроби, затем записать большее число над меньшим.
Например вычтем столбиком из десятичной дроби 123.478 целое число 56
123.478 — 56 = 67.478
..00000
—123.478
56.000
67.478
Начинаем последовательно вычитать справа налево
1) 8 – 0 = 8. Запишем 8.
2) 7 – 0 = 7. Запишем 7.
3) 4 – 0 = 4. Запишем 4.
4) Ставим точку.
5) Из числа 3 не вычесть число 6, поэтому занимаем единицу у числа 2 и ставим над ним точку. 13 – 6 = 7. Запишем число 7.
6) Над числом 2 стоит точка, значит теперь там уже не число 2, а число 1. Из единицы число 5 не вычесть, поэтому занимаем единицу у числа 1 и ставим над ним точку. 11 – 5 = 6. Запишем число 6.
7) Над числом 1 стоит точка, следовательно, 1 – 1 = 0, поэтому на этом решение законченно.
Ответ: 67.478
Еще один пример на вычитание столбиком десятичной дроби из целого числа.
432 — 2.95
432 — 2.95 = 429.05
0..0.0
—432.00
2.95
429.05
1) Из ноля число 5 не вычесть, поэтому займем единицу у ноля и поставим над ним точку, далее, как мы уже знаем ставим точку над числом 2 и занимаем единицу. 10 – 5 = 5. Запишем число 5.
2) Над числом 0 стоим точка, следовательно, 0 превратился в число 9. 9 – 9 = 0. Запишем 0.
3) Над числом два стоит точка значит 2-1 = 1. Из числа 1 число 2 не отнять, поэтому занимаем единицу у числа 3 и ставим над ним точку. 11 – 2 = 9. Запишем число 9.
4) Над числом 3 стоит точка, 3 – 1 = 2. Так как нет вычитаемого, просто сносим число 2 вниз, тоже делаем и с числом 4.
Ответ: 429.05
Правила вычитания десятичной дроби из десятичной дроби, такие же как при сложении. Нам так же необходимо сначала совместить точки десятичных дробей и затем выполнить последовательное вычитание справа налево. Вот несколько примеров на вычитание десятичных дробей:
378.326 — 26.57 = 351.756
00.0.00
—378.326
26.570
351.756
0.07 — 0.009 = 0.061
000.0
—0.070
0.009
0.061
Как умножать столбиком
Для того, чтобы умножить одно число на другое необходимо записать первый множитель над вторым, причем не важно какой множитель больше первый или второй, но удобнее чтобы записать более компактное решение записать большее число над меньшим. Затем необходимо каждое число нижнего множителя умножить на каждое число верхнего справа налево, затем суммировать произведения.
На примере будет намного понятнее. Итак, умножим 367 на 12
367 × 12 = 4404
×367
12
734
3670
4404
1. Умножим число 2 на 367 и результат запишем с справа налево от числа 2.
1) 2 × 7 = 14. Запишем число 4, число 1 в уме.
2) 2 × 6 = 12; 12 + 1 = 13. Запишем 3, число 1 в уме.
3) 2 × 3 = 6; 6 + 1 = 7. Запишем число 7. На этом этапе мы получили число 734.
2. Умножим число 1 на 367 и результат запишем справа на лево начиная уже от числа 1 под первой строкой.
1) 1 × 7 = 7. Запишем число 7.
2) 1 × 6 = 6. Запишем число 6.
3) 1 × 3 = 3. Запишем число 3. На этом этапе мы получили число 367
3. Теперь нам необходимо сложить получившиеся два числа 734 и 367
1) Под числом 4 нет слагаемого, поэтом просто снесем его вниз. Запишем число 4.
2) 3 + 7 = 10. Запишем 0 и запомним число 1.
3) 7 + 6 + 1 = 14. Запишем число 4, число 1 в уме.
4) У числа три нет слагаемого, поэтому просто запишет число 3.
На этом решение закончено, получилось 4404.
Как умножать столбиком десятичные дроби
Десятичные дроби столбиком умножать очень просто. Прежде всего, уберем точки из десятичных дробей. Затем произведем умножение уже получившихся целых чисел, далее посчитаем количество чисел в первом и во втором множителе, сложим эти значения, результатом будет число равное количеству чисел после точки в получившемся произведении. На примерах все станет намного понятнее.
Умножим 0.2354 на 12.3997
Уберем точки из десятичных дробей, чтобы было удобной умножать.
×123997
2354
495988
6199850
37199100
247994000
291888938
Теперь добавим точку в получившейся ответ. Так как в первом множителе 12.3997 после точки стоит 4 числа, и во втором множителе 0.2354 стоит 4 числа, тогда 4 + 4 = 8. Сдедовательно в ответе после точки будет 8 чисел.
2.91888938
×12.3997
0.2354
2.91888938
Умножим 49.265 на 0.0045
Уберем точки из десятичных дробей, чтобы было удобной умножать.
×49265
45
246325
1970600
2216925
Теперь добавим точку в получившейся ответ. Так как в первом множителе 49.265 после точки стоит 3 числа, а во втором множителе 0.0045 стоит 4 числа, тогда 3 + 4 = 7. Сдедовательно в ответе после точки будет 7 чисел.
0.2216925
×49.265
0.0045
0.2216925
Как делить столбиком
Как делить столбиком целые числа.
Деление столбиком с остатком, в данном материале рассматриваться не будет, если интересно, есть много информации по остатку от деления тут.
Разберем для начала как разделить большее число на меньшее в столбик (когда делимое больше делителя).
На примере будет намного нагляднее изучить данную тему. Итак, разделим 12 на 5
12 : 5 = 2.4
01205
01002.4
0020
0020
0000
При делении числа 12 на число 5 у нас получится конечная десятичная дробь. Кому интересно почитать что такое десятичные дроби — это можно сделать здесь.
1) Сколько раз число 5 помещается в числе 12? Правильно 2 раза. Поэтому первым делом умножим 2 на 5 получим 10.
2) Теперь отнимем из числа 12 число 10; 12 – 10 = 2. Запишем число 2.
3) В числе 12 нет больше чисел, поэтому поле числа 2 в ответе необходимо поставить точку. Целую часть ответа мы уже нашли! Двигаемся дальше.
4) Теперь будем находить дробную часть нашей десятичной дроби. Поставим ноль рядом с разностью. Получим число 20. Теперь снова думаем, сколько раз число 5 содержится в числе 20? Правильно 4 раза. 5 × 4 = 20.
5) Отнимем от числа 20 число 20; 20 – 20 = 0. Разность равна нулю, следовательно, результатом деления является конечная десятичная дробь.
Ответ: 2.4
Возьмем другой пример, где уже ответом будет являться бесконечная периодическая десятичная дробь. Разделим 7 на 3
7 : 3 = 2.(3)
0703
0602.3
010
009
001
1) В числе 7 число 3 содержится 2 раза. То есть неполное частное деления числа 7 на число 3 равно числу 2. Умножим число 2 на делитель. 2 × 3 = 6.
2) Отнимем от числа 7 число 6; 7 — 6 = 1; В делимом больше нет чисел, поэтому ставим точку.
3) Начинаем вычислять ответ для дробной части. Для этого к получившейся разности добавим ноль, получим число 10. Неполное частное деления числа 10 на число 3 равно числу 3. Запишем число 3 после точки.
4) 3 × 3 = 9. Из числа 10 отнимем число 9; 10 – 9 = 1. На этом этапе необходимо завершить деление, так как мы уже получали число 1 при вычитании числа 6 из числа 7, следовательно, при дальнейшем решении примера мы снова и снова будем получать число три в виде неполного частного и этот процесс будет продолжаться бесконечно (2.333333333333333333333333333…). Такое повторение называется периодом бесконечной периодической десятичной дроби. Для краткости период записывают в скобках 2.(3)
Деление десятичных дробей в столбик примеры
Разделим 3.12 на 3.6
Если числитель и знаменатель дроби умножить на одно и тоже число, то значение дроби не изменится, поэтому, чтобы было проще разделить одно число на другое, уберем запятую, домножив оба числа на 100
07120360
036001.97
03520
03240
002800
002520
000280
Разделим 9.4 на 45.1
Если числитель и знаменатель дроби умножить на одно и тоже число, то значение дроби не изменится, поэтому, чтобы было проще разделить одно число на другое, уберем запятую, домножив оба числа на 10
0940451
00000.2084257206
0940
0902
003800
003608
0001920
0001804
00001160
00000902
000002580
000002255
0000003250
0000003157
00000000930
00000000902
0000000002800
0000000002706
0000000000094
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы (Теория чисел) |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Примеры по математике для 1, 2, 3 класса
1-й класс 2-й класс 3-й класс1 класс
В первом классе начинается обучение счёту. Сначала ученикам дают примеры в пределах первой десятки — сложение и вычитание. Когда примеры с однозначными числами решаются уверенно — добавляются примеры с переходом через десяток.
Для тренировки навыков устного счёта удобно воспользоваться генератором примеров:
Примеры на сложение и вычитание в пределах 10
Вычитание однозначных чисел
Примеры на сложение и вычитание в пределах 20
Сложение и вычитание однозначных и двузнычных чисел
Примеры на сложение и вычитание в пределах 100
Сложение и вычитание двузначных чисел
2 класс
Во втором классе изучают таблицу умножения, постепенно проходя каждую цифру доводят навыки умножение для автоматизма.
Для лучшего запоминания рекомендутся давать много разнообразных примеров вперемешку. В это поможет генератор примеров на умножение:
Примеры на умножение однозначных чисел
Сумма не превышает 10
Примеры на умножение однозначных и двузначных чисел
Сумма не превышает 10
Помимо умножения во втором классе появляются примеры с пропусками значений — прообраз уравнений с одним неизвестным. В примерах с пропусками значений сначала необходимо правильно подобрать математическое действие, и только потом можно решить пример. Довести навыки счёта до автоматизмав поможет генератор примеров с пропусками значений.
Примеры на сложение и вычитание с пропусками двузначных и однозначных чисел
Сумма не превышает 10
Примеры на сложение и вычитание с пропусками двузначных чисел
Сумма не превышает 10
Примеры на сложение и вычитание с пропусками в пределах 1000
Сложение двузначных чисел с суммой не превышащей 100
Более слодные примеры — неравенства, где для решения нужно вычислить значения в левой и правой части. Это усложнённый вариант обычных примеров.
Неравенства с примерами с однозначными числами
Сумма не превышает 10
Неравенства с примерами с двузначными числами
Сумма не превышает 10
3 класс
В третьем классе продолжается отработка навыков счёта. Примеры становятся более сложными, и для их решения применяется решение в столбик. Для развития навыков быстрого счёта рекомендутся давать ученику большое количество разнообразных примеров. Их можно взять здесь:
Примеры на сложение и вычитание в пределах 1000
Сложение двузначных чисел с суммой не превышащей 100
Примеры на сложение и вычитание в пределах 10000
Сложение двузначных чисел с суммой не превышащей 1000
Примеры на сложение и вычитание с пропусками в пределах 1000
Сложение двузначных чисел с суммой не превышащей 1000
Примеры на сложение и вычитание с пропусками в пределах 10000
Сложение двузначных чисел с суммой не превышащей 10000
Примеры на умножение в третьем классе включают уже двузначные числа. Также полезно отработать счёт с «опорными» числами, которые часто встречаются в различных расчётах.
Примеры на умножение однозначных и двузначных чисел
Сумма не превышает 10
Примеры на умножение опорных чисел «12», «15», «25», «75», «125»
Сумма не превышает 10
Решения Уравнений
Что такое уравнение?
Уравнение говорит, что две вещи равны. Он будет иметь знак равенства «=», например:
Это уравнение говорит: то, что слева (х — 2) равно тому, что справа (4)
Итак, уравнение похоже на утверждение «, это равно , что »
Что такое решение?
Решение — это значение, которое мы можем поместить вместо переменной (например, x ), которая делает уравнение истинным .
Пример: х — 2 = 4
Когда мы ставим 6 вместо x, мы получаем:
6 — 2 = 4
, что правда
Таким образом, х = 6 является решением.
Как насчет других значений для х?
- Для x = 5 мы получаем «5−2 = 4», что составляет , а не , поэтому x = 5 не является решением .
- Для x = 9 мы получаем «9-2 = 4», что составляет , а не , поэтому x = 9 не является решением .
- и т. Д.
В этом случае х = 6 является единственным решением.
Вы можете попрактиковаться в решении некоторых анимированных уравнений.
Больше, чем одно решение
Может быть больше, чем одно решение .
Пример: (х-3) (х-2) = 0
Когда х равен 3, мы получаем:
(3–3) (3–2) = 0 × 1 = 0
, что является истинным
И когда х равен 2, мы получаем:
(2-3) (2-2) = (-1) × 0 = 0
, что также правда
Итак, решения:
x = 3 или x = 2
Когда мы собираем все решения вместе, это называется Solution Set
Вышеуказанный набор решений: {2, 3}
решения везде!
Некоторые уравнения верны для всех допустимых значений и затем называются . Тождества
.Пример: sin (−θ) = −sin (θ) является одним из тригонометрических тождеств
Давайте попробуем θ = 30 °:
sin (−30 °) = −0.5 и
−sin (30 °) = −0,5
Так что это истинно для θ = 30 °
Давайте попробуем θ = 90 °:
sin (−90 °) = -1 и
−sin (90 °) = −1
Так что это также истинно для θ = 90 °
Верно ли для все значения ? Попробуйте некоторые значения для себя!
Как решить уравнение
Не существует «одного идеального способа» решения всех уравнений.
Полезная цель
Но мы часто добиваемся успеха, когда наша цель —
Другими словами, мы хотим переместить все, кроме «x» (или любого другого имени переменной) в правую часть.
Пример: Решить 3x − 6 = 9
Начать с: 3x − 6 = 9
Добавьте 6 к обеим сторонам: 3x = 9 + 6
Разделите на 3: x = (9 + 6) / 3
Теперь у нас есть x = что-то ,
и короткий расчет показывает, что х = 5
как пазл
На самом деле, решение уравнения — это как решение головоломки.И как головоломки, есть вещи, которые мы можем (и не можем) делать.
Вот некоторые вещи, которые мы можем сделать:
Пример: Solve √ (x / 2) = 3
Начните с: √ (x / 2) = 3
Квадрат с обеих сторон: х / 2 = 3 2
Рассчитать 3 2 = 9: х / 2 = 9
Умножим обе стороны на 2: x = 18
И чем больше уловок и техник вы изучите, тем лучше вы получите.
Специальные уравнения
Существуют специальные способы решения некоторых типов уравнений.Узнайте, как …
Проверьте свои решения
Вы должны всегда проверять, действительно ли ваше «решение» является решением .
Как проверить
Возьмите решения и поместите их в исходное уравнение , чтобы увидеть, действительно ли они работают.
Пример: решите для х:
2x x — 3 + 3 = 6 x — 3 (x) 3)
Мы сказали, что x ≠ 3, чтобы избежать деления на ноль.
Давайте умножим на (х — 3):
2x + 3 (x − 3) = 6
Принесите 6 слева:
2x + 3 (x − 3) — 6 = 0
Развернуть и решить:
2x + 3x — 9 — 6 = 0
5x — 15 = 0
5 (х — 3) = 0
x — 3 = 0
Это можно решить, имея х = 3
Давайте проверим:
2 × 3 3 — 3 + 3 = 6 3 — 3
Держись!
Это означает деление на ноль!
И в любом случае, мы сказали наверху, что x ≠ 3, так что…
x = 3 на самом деле не работает, и так:
Существует Нет Решение!
Это было интересно … мы думали, что мы нашли решение, но когда мы оглянулись на вопрос, мы обнаружили, что это не разрешено!
Это дает нам моральный урок:
«Решение» только дает нам возможные решения, их нужно проверять!
Советы
- Запишите, где выражение не определено (из-за деления на ноль, квадратного корня из отрицательного числа или по какой-либо другой причине)
- Покажите все шаги , чтобы его можно было проверить позже (вами или кем-то еще)
Введите уравнение вместе с переменной, для которой вы хотите его решить, и нажмите кнопку «Решить».
В этой главе мы разработаем определенные методы, которые помогут решить проблемы, изложенные в словах. Эти методы включают переписывание задач в виде символов. Например, заявленная проблема
«Найти число, которое при добавлении к 3 дает 7»
может быть записано как:
3+? = 7, 3 + n = 7, 3 + x = 1
и так далее, где символы?, N и x представляют число, которое мы хотим найти.Мы называем такие сокращенные версии поставленных задач уравнениями или символическими предложениями. Уравнения, такие как x + 3 = 7, являются уравнениями первой степени, так как переменная имеет показатель степени 1. Члены слева от знака равенства составляют левый член уравнения; те, что справа, составляют правый член. Таким образом, в уравнении x + 3 = 7 левый элемент равен x + 3, а правый элемент равен 7.
РЕШЕНИЕ УРАВНЕНИЙ
Уравнения могут быть истинными или ложными, так же как словосочетания могут быть истинными или ложными.Уравнение:
3 + х = 7
будет ложным, если вместо переменной подставлено любое число, кроме 4. Значение переменной, для которой уравнение истинно (в данном примере 4), называется решением уравнения. Мы можем определить, является ли данное число решением данного уравнения, подставляя вместо переменной число и определяя истинность или ложность результата.
Пример 1 Определите, является ли значение 3 решением уравнения
4x — 2 = 3x + 1
Решение Подставим значение 3 для x в уравнении и посмотрим, равен ли левый член правому члену.
4 (3) — 2 = 3 (3) + 1
12 — 2 = 9 + 1
10 = 10
Отв. 3 является решением.
Уравнения первой степени, которые мы рассмотрим в этой главе, имеют не более одного решения. Решения многих таких уравнений могут быть определены путем проверки.
Пример 2 Найти решение каждого уравнения путем проверки.
а. х + 5 = 12
б. 4 · х = -20
Решения а. 7 является решением, так как 7 + 5 = 12.
б. -5 является решением, так как 4 (-5) = -20.
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ ДОБАВЛЕНИЯ И ВЫЧИСЛЕНИЯ
В разделе 3.1 мы решили некоторые простые уравнения первой степени путем проверки. Однако решения большинства уравнений не сразу очевидны при проверке. Следовательно, нам нужны математические «инструменты» для решения уравнений.
Эквивалентные уравнения
Эквивалентные уравнения — это уравнения с одинаковыми решениями. Таким образом,
3x + 3 = x + 13, 3x = x + 10, 2x = 10 и x = 5
являются эквивалентными уравнениями, потому что 5 является единственным решением каждого из них.Обратите внимание, что в уравнении 3x + 3 = x + 13 решение 5 не видно при проверке, но в уравнении x = 5 решение 5 очевидно при проверке. При решении любого уравнения мы преобразуем данное уравнение, решение которого может быть неочевидным, в эквивалентное уравнение, решение которого легко заметить.
Следующее свойство, которое иногда называют свойством сложения-вычитания , является одним из способов, которым мы можем генерировать эквивалентные уравнения.
Если к обоим элементам добавляется или вычитается одинаковое количество уравнения, полученное уравнение эквивалентно исходному уравнение.
В символах,
a — b, a + c = b + c и a — c = b — c
являются эквивалентными уравнениями.
Пример 1 Напишите уравнение, эквивалентное
х + 3 = 7
путем вычитания 3 от каждого члена.
Решение Вычитание 3 из каждого члена дает
х + 3 — 3 = 7 — 3
или
х = 4
Обратите внимание, что x + 3 = 7 и x = 4 являются эквивалентными уравнениями, поскольку решение одинаково для обоих, а именно 4.Следующий пример показывает, как мы можем генерировать эквивалентные уравнения, сначала упрощая один или оба члена уравнения.
Пример 2 Напишите уравнение, эквивалентное
4x- 2-3x = 4 + 6
путем объединения одинаковых терминов, а затем добавив 2 к каждому члену.
Объединение одинаковых терминов дает
х — 2 = 10
Добавление 2 к каждому члену дает
х-2 + 2 = 10 + 2
х = 12
Чтобы решить уравнение, мы используем свойство сложения-вычитания, чтобы преобразовать данное уравнение в эквивалентное уравнение вида x = a, из которого мы можем найти решение путем проверки.
Пример 3 Решить 2x + 1 = x — 2.
Мы хотим получить эквивалентное уравнение, в котором все члены, содержащие x, находятся в одном члене, а все члены, не содержащие x, находятся в другом. Если мы сначала добавим -1 к каждому члену (или вычтем 1 из), мы получим
2x + 1- 1 = x — 2- 1
2x = x — 3
Если теперь мы добавим -x к каждому члену (или вычтем x), мы получим
2x-x = x — 3 — x
х = -3
, где решение -3 очевидно.
Решением исходного уравнения является число -3; однако ответ часто отображается в виде уравнения х = -3.
Поскольку каждое уравнение, полученное в процессе, эквивалентно исходному уравнению, -3 также является решением 2x + 1 = x — 2. В приведенном выше примере мы можем проверить решение, подставив — 3 для x в исходном уравнении
2 (-3) + 1 = (-3) — 2
-5 = -5
Симметричное свойство равенства также полезно при решении уравнений. Это свойство заявляет
Если a = b, то b = a
Это позволяет нам обмениваться элементами уравнения всякий раз, когда мы хотим, без необходимости каких-либо изменений знака.Таким образом,
Если 4 = x + 2, то x + 2 = 4
Если x + 3 = 2x — 5, то 2x — 5 = x + 3
Если d = rt, то rt = d
Может быть несколько различных способов применить свойство сложения выше. Иногда один метод лучше другого, а в некоторых случаях симметричное свойство равенства также полезно.
Пример 4 Решить 2x = 3x — 9. (1)
РешениеЕсли мы сначала добавим -3x к каждому члену, мы получим
2x — 3x = 3x — 9 — 3x
-х = -9
, где переменная имеет отрицательный коэффициент.Хотя мы можем видеть из проверки, что решение равно 9, потому что — (9) = -9, мы можем избежать отрицательного коэффициента, добавив -2x и +9 к каждому члену уравнения (1). В этом случае мы получаем
2x-2x + 9 = 3x- 9-2x + 9
9 = х
, из которого решение 9 очевидно. Если мы хотим, мы можем записать последнее уравнение как x = 9 с помощью симметричного свойства равенства.
РЕШЕНИЕ УРАВНЕНИЙ С ИМУЩЕСТВЕННЫМ ИМУЩЕСТВОМ
Рассмотрим уравнение
3x = 12
Решение этого уравнения 4.Также обратите внимание, что если мы разделим каждый член уравнения на 3, мы получим уравнения
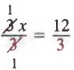
, решение которого также равно 4. В общем, мы имеем следующее свойство, которое иногда называют свойством деления.
Если оба члена уравнения разделены одинаковыми (ненулевыми) количество, полученное уравнение эквивалентно исходному уравнению.
В символах,
являются эквивалентными уравнениями.
Пример 1 Напишите уравнение, эквивалентное
-4x = 12
путем деления каждого члена на -4.
РешениеДеление обоих членов на -4 дает
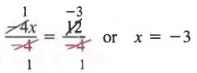
При решении уравнений мы используем указанное выше свойство для получения эквивалентных уравнений, в которых переменная имеет коэффициент 1.
Пример 2 Решить 3y + 2y = 20.
Сначала мы объединяем подобные термины, чтобы получить
5y = 20
Затем, разделив каждого члена на 5, мы получим
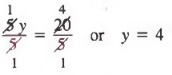
В следующем примере мы используем свойство сложения-вычитания и свойство деления для решения уравнения.
Пример 3 Решить 4x + 7 = x — 2.
РешениеСначала мы добавляем -x и -7 к каждому члену, чтобы получить
4x + 7 — x — 7 = x — 2 — x — 1
Далее, объединение одинаковых терминов дает
3x = -9
Наконец, мы делим каждого члена на 3, чтобы получить
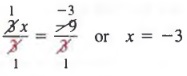
РЕШЕНИЕ УРАВНЕНИЙ С ИМУЩЕСТВОМ МНОЖЕНИЯ
Рассмотрим уравнение
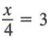
Решение этого уравнения — 12. Также обратите внимание, что если мы умножим каждый член уравнения на 4, мы получим уравнения
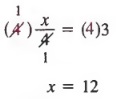
, чье решение также 12.В общем, мы имеем следующее свойство, которое иногда называют свойством умножения.
Если оба члена уравнения умножаются на одну и ту же ненулевую величину, результирующее уравнение эквивалентно исходному уравнению.
В символах,
a = b и a · c = b · c (c ≠ 0)
являются эквивалентными уравнениями.
Пример 1 Напишите эквивалентное уравнение для
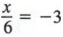
путем умножения каждого члена на 6.
РешениеУмножение каждого члена на 6 дает
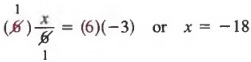
При решении уравнений мы используем указанное выше свойство для получения эквивалентных уравнений, которые не содержат дробей.
Пример 2 Решить 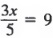
Сначала умножьте каждого члена на 5, чтобы получить
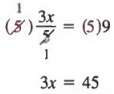
Теперь разделите каждого члена на 3,
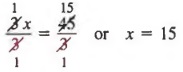
Пример 3 Решить 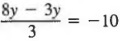 .
.
Во-первых, упростите над дробной чертой, чтобы получить
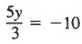
Затем умножьте каждого члена на 3, чтобы получить
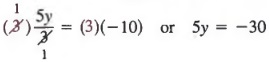
Последнее, разделив каждого члена на 5, получим
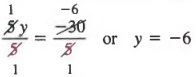
ДАЛЬНЕЙШИЕ РЕШЕНИЯ УРАВНЕНИЙ
Теперь мы знаем все методы, необходимые для решения большинства уравнений первой степени.Нет определенного порядка, в котором должны применяться свойства. Любой из следующих шагов, перечисленных на стр. 102, может быть подходящим.
Шаги для решения уравнений первой степени:
- Объедините одинаковые термины в каждом члене уравнения.
- Используя свойство сложения или вычитания, напишите уравнение со всеми терминами, содержащими неизвестное в одном элементе, и всеми терминами, не содержащими неизвестное в другом.
- Объедините одинаковые термины в каждом члене.
- Используйте свойство умножения для удаления дробей.
- Используйте свойство деления для получения коэффициента 1 для переменной.
Пример 1 Решить 5x — 7 = 2x — 4x + 14.
РешениеСначала мы объединяем одинаковые термины, 2x — 4x, чтобы получить
5x — 7 = -2x + 14
Далее, мы добавляем + 2x и +7 к каждому члену и объединяем одинаковые условия, чтобы получить
5x — 7 + 2x + 7 = -2x + 14 + 2x + 1
7x = 21
Наконец, мы делим каждого члена на 7, чтобы получить
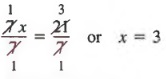
В следующем примере мы упрощаем выше дробной черты перед применением свойств, которые мы изучали.
Пример 2 Решить 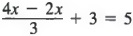
Сначала мы объединяем одинаковые термины, 4x — 2x, чтобы получить
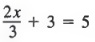
Затем мы добавляем -3 к каждому члену и упрощаем
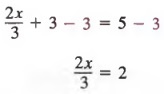
Далее, мы умножаем каждого члена на 3, чтобы получить

Наконец, мы делим каждого члена на 2, чтобы получить
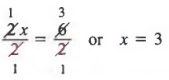
ФОРМУЛА РЕШЕНИЯ
Уравнения, которые включают переменные для мер двух или более физических величин, называются формулами.Мы можем решить для любой из переменных в формуле, если известны значения других переменных. Мы подставляем известные значения в формулу и определяем неизвестную переменную методами, которые мы использовали в предыдущих разделах.
Пример 1 В формуле d = rt найдите t, если d = 24 и r = 3.
РешениеМы можем решить для t, подставив 24 для d и 3 для r. То есть
д = кт
(24) = (3) т
8 = т
Часто необходимо решить формулы или уравнения, в которых имеется более одной переменной для одной из переменных в терминах других.Мы используем те же методы, что и в предыдущих разделах.
Пример 2 В формуле d = rt решите для t через r и d.
РешениеМы можем решить для t в терминах r и d, разделив оба члена на r, чтобы получить
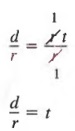
из которых по симметричному закону
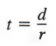
В приведенном выше примере мы решили для t, применяя свойство деления для генерации эквивалентного уравнения. Иногда необходимо применять более одного такого свойства.
Пример 3 В уравнении ax + b = c решите для x через a, b и c.
РешениеМы можем решить для х, сначала добавив -b к каждому члену, чтобы получить
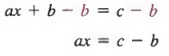
затем разделив каждого члена на, у нас есть
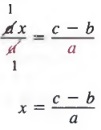
Math Equation Solver
Использование калькулятора
Решите математические задачи, используя порядок операций, таких как PEMDAS, BEDMAS и BODMAS. (Предупреждение PEMDAS) Этот калькулятор решает математические уравнения, которые складывают, вычитают, умножают и делят положительные и отрицательные числа и показательные числа. Вы также можете включить скобки и числа с показателями или корнями в ваши уравнения.5 — это 2, возведенные в степень 5)
r Корни (2r3 — третий корень из 2)
() [] {} Кронштейны
Вы можете попытаться скопировать уравнения из других печатных источников и вставить их здесь, и, если они используют ÷ для деления и × для умножения, этот калькулятор уравнений попытается преобразовать их в / и * соответственно, но в некоторых случаях вам может потребоваться повторить ввод скопированные и вставленные символы или даже полные уравнения.(2/3) 5 поднял до 2/3
Ввод фракций
Если вы хотите, чтобы запись, такая как 1/2, рассматривалась как дробь, введите ее как (1/2). Например, в уравнении 4, деленном на ½, вы должны ввести его как 4 / (1/2). Затем сначала выполняется деление 1/2 = 0,5, а последнее — 4 / 0,5 = 8. Если вы неправильно введете его как 4/1/2, то сначала решается 4/1 = 4, а затем 4/2 = 2.2 неправильный ответ. 8 был правильный ответ.
математический порядок операций — PEMDAS, BEDMAS, BODMAS
PEMDAS — это сокращение, которое может помочь вам вспомнить порядок операций для решения математических уравнений. PEMDAS типично расширяется до фразы «Пожалуйста, извините мою дорогую тетю Салли». Первая буква каждого слова в фразе создает аббревиатуру PEMDAS. Решите математические задачи с помощью стандартного математического порядка операций, работая слева направо:
- Скобки — работая слева направо в уравнении, сначала найдите и решите выражения в скобках; если у вас есть вложенные скобки, то работайте от самого внутреннего до
- Экспоненты и корни — работая слева направо в уравнении, вычислить все экспоненциальные и корневые выражения секунды
- Умножение и деление — затем решайте одновременно выражения умножения и деления, работая в уравнении слева направо.
- сложение и вычитание — затем, решите одновременно оба выражения сложения и вычитания, работая слева направо в уравнении
PEMDAS Предупреждение
Умножение не всегда выполняется перед делением. Умножение и деление происходят одновременно, слева направо.
Сложение не всегда выполняется перед вычитанием. Сложение и вычитание происходят одновременно, слева направо.
Порядок «MD» (DM в BEDMAS) иногда путают в значении умножения перед делением (или наоборот). Тем не менее, умножение и деление имеют одинаковый приоритет. Другими словами, умножение и деление выполняются в течение одного и того же шага слева направо. Например, 4/2 * 2 = 4 и 4/2 * 2 не равно 1.
Такая же путаница может произойти и с «AS», однако сложение и вычитание также имеют одинаковый приоритет и выполняются в течение одного и того же шага слева направо.Например, 5 — 3 + 2 = 4 и 5 — 3 + 2 не равно 0.
Чтобы запомнить это, можно написать PEMDAS как PE (MD) (AS) или BEDMAS как BE (DM) (AS).
Порядок действий Сокращения
Сокращения порядка операций означают, что вы должны решать уравнения в этом порядке, всегда работая слева направо в вашем уравнении.
PEMDAS означает P , E компонентов, M с ультипликацией и D ivision, A ddition и S «» «
»Вы также можете увидеть BEDMAS и BODMAS как порядок действий.В этих сокращениях «квадратные скобки» совпадают с круглыми скобками, а «порядок» совпадает с показателями степени.
BEDMAS означает « B ракеток, E компонентов, D ivision и M ultiplication, A ddition и S «» «
» ФИЛЬМЫ ПОХОЖИЕ НА БОДМАСBODMAS означает « B ракеток, O , D ivision и M ultiplication, A ddition и S «» «
»Оперативность Ассоциация
Умножение, деление, сложение и вычитание левоассоциативны.Это означает, что когда вы решаете выражения умножения и деления, вы переходите от левой части уравнения к правой. Точно так же, когда вы решаете выражения сложения и вычитания, вы продолжаете слева направо.
Примеры левой ассоциативности:
- a / b * c = (a / b) * c
- a + b — c = (a + b) — c
Экспоненты и корни или радикалы являются ассоциативными справа и решаются справа налево.(4/5))
Для вложенных скобок или скобок, сначала решите самые внутренние скобки или выражения в скобках и работайте с внешними скобками. Для каждого выражения в скобках следуйте остальной части порядка PEMDAS: сначала вычислите показатели и радикалы, затем умножение и деление, и, наконец, сложение и вычитание.
Вы можете решить умножение и деление во время одного и того же шага в математической задаче: после решения для скобок, показателей и радикалов и до сложения и вычитания.Продолжайте слева направо для умножения и деления. Решите сложение и вычитание последним после скобок, показателей, корней и умножения / деления. Снова, продолжайте слева направо для сложения и вычитания.
Сложение, вычитание, умножение и деление положительных и отрицательных чисел
Этот калькулятор следует стандартным правилам для решения уравнений.
Правила для операций добавления (+)
Если знаки совпадают, сохраните знак и добавьте цифры.
-21 + -9 = — 30
(+7) + (+13) = (+20)
Если знаки отличаются, то вычтите меньшее число из большего числа и оставьте знак большего числа.
(-13) + (+5) = (-8)
(-7) + (+9) = (+2)
Правила вычитания операций (-)
Сохраняй знак первого числа.Замените все следующие знаки вычитания на знаки сложения. Измените знак каждого следующего числа так, чтобы положительное стало отрицательным, а отрицательное стало положительным, затем следуйте правилам для проблем сложения.
(-15) — (-7) =
(-5) — (+6) =
(+4) — (-3) =
(-15) + (+7) = (-8)
(-5) + (-6) = (-11)
(+4) + (+3) = (+7)
Правила для операций умножения (* или ×)
Умножение отрицательного числа на отрицательное или положительного на положительное дает положительный результат.Умножение положительного на отрицательное или отрицательного на положительное приводит к отрицательному результату.
-10 * -2 = 20
10 * 2 = 20
10 * -2 = -20
-10 * 2 = -20
-10 × -2 = 20
10 × 2 = 20
10 × -2 = -20
-10 × 2 = -20
Правила для операций подразделения (/ или ÷)
Подобно умножению, деление отрицательного на отрицательное или положительного на положительное дает положительный результат.Разделение положительного на отрицательное или отрицательное на положительное приводит к отрицательному результату.
-10 / -2 = 5
10/2 = 5
10 / -2 = -5
-10 / 2 = -5
-10 ÷ -2 = 5
10 ÷ 2 = 5
10 ÷ -2 = -5
-10 ÷ 2 = -5
,Введите полиномиальное неравенство вместе с переменной, для которой нужно найти решение, и нажмите кнопку «Решить».
В главе 2 мы установили правила для решения уравнений с использованием чисел арифметики. Теперь, когда мы изучили операции со знаковыми числами, мы будем использовать те же правила для решения уравнений с отрицательными числами. Мы также изучим методы решения и построения графиков неравенств, имеющих одно неизвестное.
РЕШЕНИЕ УРАВНЕНИЙ С УЧЕТОМ НОМЕРОВ
ЦЕЛЕЙ
По завершении этого раздела вы сможете решать уравнения, включающие числа со знаком.
Пример 1 Решите для х и проверьте: х + 5 = 3
Решение
Используя те же процедуры, что и в главе 2, мы вычитаем 5 с каждой стороны уравнения, получая
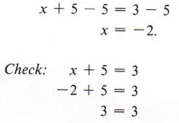
Пример 2 Решите для х и проверьте: — 3х = 12
Решение
Разделив каждую сторону на -3, получим
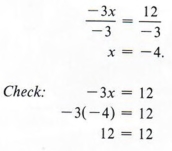
| Всегда проверяйте в исходном уравнении. |

| Другой способ решения уравнения 3x — 4 = 7x + 8 — сначала вычесть 3x с обеих сторон, получив -4 = 4x + 8, , затем вычесть 8 с обеих сторон и получить -12 = 4x , Теперь разделите обе стороны на 4, получив — 3 = x или x = — 3. |

| Сначала удалите скобки. Затем следуйте процедуре, описанной в главе 2. |
ЛИТЕРАЛЬНЫЕ УРАВНЕНИЯ
ЦЕЛЕЙ
По завершении этого раздела вы сможете:
- Определите буквальное уравнение.
- Применение ранее изученных правил для решения буквальных уравнений.
Уравнение, имеющее более одной буквы, иногда называется буквальным уравнением . Иногда необходимо решить такое уравнение для одной буквы с точки зрения других. Пошаговая процедура, обсуждаемая и используемая в главе 2, остается в силе даже после удаления любых символов группировки.
Пример 1 Решить для c: 3 (x + c) — 4y = 2x — 5c
Решение
Сначала удалите скобки.
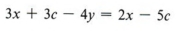
В этот момент мы отмечаем, что, поскольку мы решаем для c, мы хотим получить c с одной стороны и все другие члены с другой стороны уравнения. Таким образом, мы получаем
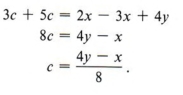

| Помните, что abx — это то же самое, что и 1abx. Разделим на коэффициент х, который в данном случае равен ab. |

| Решите уравнение 2x + 2y — 9x + 9a, сначала вычтя 2.V с обеих сторон. Сравните решение с полученным в примере. |
Иногда форму ответа можно изменить. В этом примере мы могли бы умножить числитель и знаменатель ответа на (- l) (это не меняет значение ответа) и получить
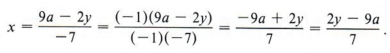
Преимущество этого последнего выражения перед первым состоит в том, что в ответе не так много отрицательных признаков.
| Умножение числителя и знаменателя дроби на одно и то же число является использованием фундаментального принципа дробей. |
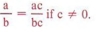
Наиболее часто используемые буквальные выражения — это формулы из геометрии, физики, бизнеса, электроники и так далее.
Пример 4 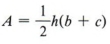 — формула для площади трапеции. Решить для ц.
— формула для площади трапеции. Решить для ц.
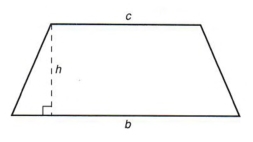

| Трапеция имеет две параллельные стороны и две непараллельные стороны. Параллельные стороны называются основаниями. Удаление скобок не означает просто стереть их. Мы должны умножить каждый член в скобках на коэффициент, предшествующий скобкам. Изменение формы ответа не является необходимым, но вы должны быть в состоянии распознать, когда у вас есть правильный ответ, даже если форма не совпадает. |
Пример 5 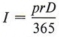 — это формула, дающая проценты (I), заработанные за период D дней, когда известны основная сумма (p) и годовая ставка (r). Найдите годовую ставку, когда сумма процентов, основная сумма и количество дней все известны.
— это формула, дающая проценты (I), заработанные за период D дней, когда известны основная сумма (p) и годовая ставка (r). Найдите годовую ставку, когда сумма процентов, основная сумма и количество дней все известны.
Решение
Задача требует решения 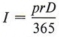 по р.
по р.
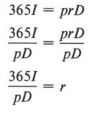
Обратите внимание, что в этом примере r было оставлено справа и, таким образом, вычисление было проще. Мы можем переписать ответ другим способом, если пожелаем.
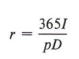
графическое неравенство
ЦЕЛЕЙ
По завершении этого раздела вы сможете:
- Используйте символ неравенства для представления взаимных позиций двух чисел в числовой строке.
- График неравенства на числовой линии.
Мы уже обсуждали набор из рациональных чисел как те, которые могут быть выражены как отношение двух целых чисел. Существует также набор чисел, называемых иррациональных чисел, , которые не могут быть выражены как отношение целых чисел. В этот набор входят такие номера, как 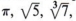 и так далее. Множество, состоящее из рациональных и иррациональных чисел, называется действительными числами .
и так далее. Множество, состоящее из рациональных и иррациональных чисел, называется действительными числами .
Учитывая любые два действительных числа a и b, всегда можно утверждать, что 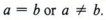 Много раз нас интересует только, равны ли два числа, но существуют ситуации, когда мы также хотим представить относительный размер чисел, которые не равный.
Много раз нас интересует только, равны ли два числа, но существуют ситуации, когда мы также хотим представить относительный размер чисел, которые не равный.
Символы представляют собой символов неравенства или отношения порядка и используются для отображения относительных размеров значений двух чисел. Обычно мы читаем символ как «больше чем». Например, a> b читается как «a больше, чем b». Обратите внимание, что мы заявили, что мы обычно читаем
а

| Какое положительное число можно добавить к 2, чтобы получить 5? |

Проще говоря, это определение гласит, что a меньше b, если мы должны добавить что-то к a, чтобы получить b.Конечно, «что-то» должно быть положительным.
Если вы думаете о числовой строке, вы знаете, что добавление положительного числа эквивалентно перемещению вправо по числовой строке. Это приводит к следующему альтернативному определению, которое может быть легче визуализировать.
Пример 1 3

| Мы могли бы также написать 6> 3. |
Пример 2 — 4

| Мы могли бы также написать 0> — 4. |
Пример 3 4> — 2, потому что 4 находится справа от -2 в числовой строке.

Пример 4 — 6

Математическое утверждение х
| Видите ли вы, почему найти наибольшее число меньше 3 невозможно? |
На самом деле, назвать число х, которое является наибольшим числом меньше 3, является невыполнимой задачей. Однако это может быть указано в числовой строке.Чтобы сделать это, нам нужен символ для обозначения значения утверждения, такой как х
Символы (и), используемые в числовой строке, указывают, что конечная точка не включена в набор.
Пример 5 График х
Решение

Обратите внимание, что на графике есть стрелка, указывающая, что линия продолжается без конца влево.
| Этот график представляет каждое действительное число меньше 3. |
Пример 6 График x> 4 на числовой линии.
Решение

| Этот график представляет каждое действительное число больше 4. |
Пример 7 График x> -5 на числовой линии.
Решение

| Этот график представляет каждое действительное число больше -5. |
Пример 8 Построить числовой линейный график, показывающий, что x> — 1 и x
Решение

Утверждение х> — 1 и х
| Этот график представляет все действительные числа в диапазоне от — 1 до 5. |
Пример 9 График — 3
Решение

Если мы хотим включить конечную точку в набор, мы используем другой символ, 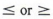 :. Мы читаем эти символы как «равно или меньше» и «равно или больше чем».
:. Мы читаем эти символы как «равно или меньше» и «равно или больше чем».
Пример 10 х>; 4 обозначает число 4 и все действительные числа справа от 4 в числовой строке.
Символы [и], используемые в числовой строке, указывают, что конечная точка включена в набор.
| Вы найдете, что использование скобок и скобок соответствует их использованию в будущих курсах математики. |

| Этот график представляет число 1 и все действительные числа больше 1. |
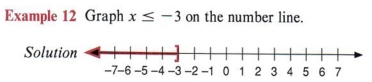
| Этот график представляет число 1 и все действительные числа, меньшие или равные — 3. |
Пример 13 Напишите алгебраическое утверждение, представленное следующим графиком.
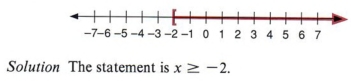
Пример 14 Напишите алгебраическое утверждение для следующего графика.
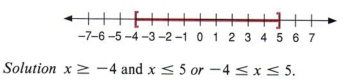
| Этот график представляет все действительные числа от -4 до 5 , включая -4 и 5. |
Пример 15 Напишите алгебраическое утверждение для следующего графика.
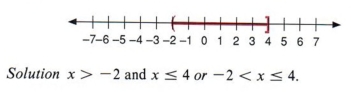
| Этот график включает 4, но , а не -2. |
Пример 16 График 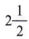 на числовой линии.
на числовой линии.
Решение
Этот пример представляет небольшую проблему. Как мы можем указать 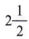 в числовой строке? Если мы оценим суть, то другой человек может неправильно понять утверждение. Не могли бы вы сказать, представляет ли точка
в числовой строке? Если мы оценим суть, то другой человек может неправильно понять утверждение. Не могли бы вы сказать, представляет ли точка 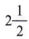 или
или 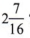 ? Поскольку целью графика является уточнение, всегда обозначает конечную точку.
? Поскольку целью графика является уточнение, всегда обозначает конечную точку.
| График используется для передачи заявления. Вы всегда должны называть нулевую точку, чтобы показать направление, а также конечную точку или точки, чтобы быть точными. |
РЕШЕНИЕ НЕРАВЕНСТВ
ЦЕЛЕЙ
По завершении этого раздела вы сможете решить неравенства, связанные с одним неизвестным.
Решения для неравенств обычно включают те же основные правила, что и уравнения. Есть одно исключение, которое мы скоро обнаружим. Первое правило, однако, аналогично тому, которое используется при решении уравнений.
Если к каждой стороне неравенства добавлено одинаковое количество, результаты будут неравными в том же порядке.
Пример 1 Если 5
Пример 2 Если 7
Мы можем использовать это правило для решения некоторых неравенств.
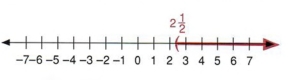
Пример 3 Решить для х: х + 6
Решение
Если мы добавим -6 к каждой стороне, мы получим
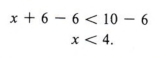
Графики этого решения на числовой линии, у нас есть


| Обратите внимание, что процедура такая же, как при решении уравнений. |
Теперь мы будем использовать правило сложения, чтобы проиллюстрировать важную концепцию, касающуюся умножения или деления неравенств.
Предположим, что x> a.
Теперь добавьте -x в обе стороны по правилу сложения.
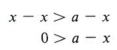
| Помните, что добавление одинакового количества к обеим сторонам неравенства не меняет его направление. |
Теперь добавьте -a в обе стороны.
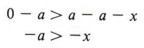
Последнее утверждение, — a> -x, может быть переписано как — x <-a.Поэтому мы можем сказать: «Если х> а, то — х
Если неравенство умножается или делится на отрицательное число , равное , результаты будут в неравном порядке в , противоположном порядку .
| Например: если 5> 3, то -5 |
Пример 5 Решите для х и построите график решения: -2x> 6
Решение
Чтобы получить x с левой стороны, мы должны разделить каждый член на — 2. Обратите внимание, что, поскольку мы делим на отрицательное число, мы должны изменить направление неравенства.
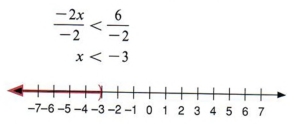
| Обратите внимание, что как только мы делим на отрицательную величину, мы должны изменить направление неравенства. |
Обратите особое внимание на этот факт. Каждый раз, когда вы делите или умножаете на отрицательное число, вы должны изменить направление символа неравенства. Это единственная разница между решением уравнений и решением неравенств.
| Когда мы умножаем или делим на положительное число, без изменений.Когда мы умножаем или делим на отрицательное число, направление неравенства меняется. Будьте осторожны — это источник многих ошибок. |
После того как мы удалили скобки и в выражении есть только отдельные термины, процедура поиска решения почти такая же, как в главе 2.
Давайте теперь рассмотрим пошаговый метод из главы 2 и отметим разницу при решении неравенств.
Первые Исключить дроби, умножив все члены на наименьший общий знаменатель из всех дробей.(Без изменений, когда мы умножаем на положительное число.)
Секунда Упростим, скомбинировав одинаковые термины на каждой стороне неравенства. (Без изменений)
Третий Сложите или вычтите количества, чтобы получить неизвестное на одной стороне и числа на другой. (Без изменений)
Четвертый Разделите каждый член неравенства на коэффициент неизвестного. Если коэффициент положительный, неравенство останется прежним. Если коэффициент отрицательный, неравенство будет обратным.(Это важное различие между уравнениями и неравенствами.)
| Единственная возможная разница заключается в последнем шаге. |

| Что нужно сделать при делении на отрицательное число? |

| Не забудьте обозначить конечную точку. |
РЕЗЮМЕ
Ключевые слова
- Буквальное уравнение — это уравнение, включающее более одной буквы.
- Символы представляют собой символов неравенства или отношений порядка .
- a a находится слева от b на линии вещественных чисел.
- Двойные символы
 : указывают, что конечные точки включены в набор решений .
: указывают, что конечные точки включены в набор решений .
процедур
- Чтобы решить буквальное уравнение для одной буквы в терминах других, выполните те же шаги, что и в главе 2.
- Для решения неравенства используйте следующие шаги:
Шаг 1 Удалите дроби, умножив все члены на наименьший общий знаменатель из всех дробей.
Шаг 2 Упростите, объединив одинаковые термины с каждой стороны неравенства.
Шаг 3 Сложите или вычтите количества, чтобы получить неизвестное на одной стороне и числа на другой.
Шаг 4 Разделите каждый член неравенства на коэффициент неизвестного. Если коэффициент положительный, неравенство останется прежним. Если коэффициент отрицательный, неравенство будет обратным.
Шаг 5 Проверьте свой ответ.
